Вероятностно-статистические аспекты метода Монте-Карло и имитационного моделирования

Как уже отмечалось выше, при решении задач методом МК или ИМ следует иметь в виду, что получаемые результаты являются фактически исходами вычислительного эксперимента. Следовательно, эти результаты должны интерпретироваться с точки зрения математической статистики. В соответствии с законом больших чисел, свойства устойчивости результаты приобретают после многократного повторения такого эксперимента. Вопрос о достаточности числа вычислительных опытов может ставиться только для конкретной системы и при известных начальных условиях. Рассмотрим пример определения площади круга из главы 1 данной работы. Выберем число наблюдений (в ИМ это число чаще называют числом прогонов модели)

N=10. Меняя продолжительность прогона от 100 до 10000 точек, вычислим средние выборочные и дисперсии для каждого из этих случаев. Для наглядности приведем программу вычислений площади круга еще раз. Результаты сведем в таблицу.

Точное значение площади круга

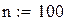
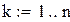
Длина прогона

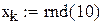
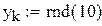
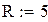
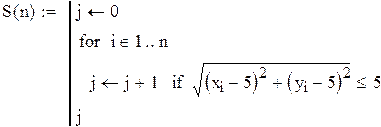
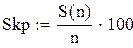
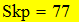
Результат единичного опыта

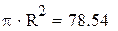
Номер опыта	Оценка площади круга при фиксированном числе n
n =100	n =200	n =500	n =1000	n =2000	n =5000	n =10000
		77.5 81.5 74.5 77.5 79.5 78.5 76.5	77.8 74.2 79.2 80.4 78.6 81.4 76.2 78.6 79.2	77.4 78.3 75.6 78.9 78.8 78.0 77.9 76.5 79.5 78.1	77.15 78.95 79.85 79.0 77.6 78.5 79.1 79.75 77.6 78.5	78.84 78.92 78.56 77.98 78.54 78.26 79.24 78.28 79.44 78.78	78.66 77.97 78.9 78.62 79.19 78.0 77.82 78.66 78.32 78.58
Среднее	75.8	77.35	78.06	77.9	78.6	78.68	78.46
Дисперсия	15.76	5.15	4.76	1.21	0.75	0.18	0.17

По данным расчетов, приведенных в таблице можно сделать следующие выводы.

1. С ростом числа генерируемых точек (продолжительности прогона модели) оценки площади круга приближаются к точному значению.

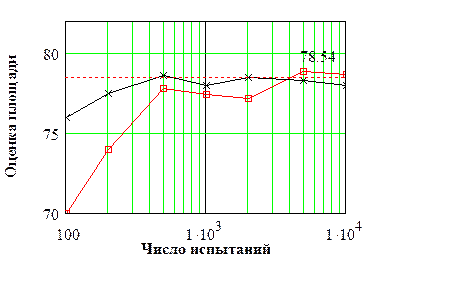
На графике показаны оценки площади круга для прогонов 1 и 6 в зависимости от продолжительности прогона. Видно, что сначала оценки испытывают сильные колебания, а затем стабилизируются вблизи точного значения. Наблюдаемое явление типично для любой имитационной модели.

2. Прогоны модели, отличающиеся друг от друга только последовательностями случайных чисел, дают различные оценки при одном и том же значении n.

3. Отметим, что влияние переходных условий уменьшается при усреднении результатов прогонов (это хорошо видно из строки таблицы для средних выборочных).

4. Дисперсия рассматриваемой случайной величины существенно уменьшается при увеличении продолжительности прогона с 100 до 200, а затем ее уменьшение незначительно. Этот факт так же характерен для имитационных моделей, что позволяет подобрать оптимальное для рассматриваемей задачи значение n, по критерию точность− затраты машинного времени.

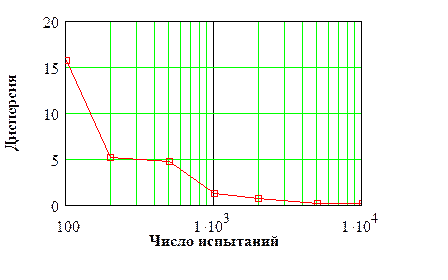
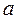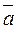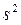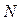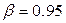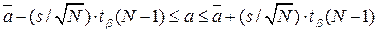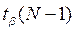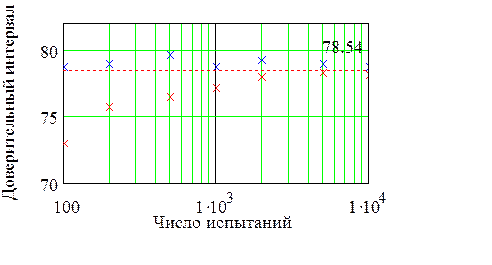
5. Наряду с точечными оценками, рассмотрим доверительные интервалы, показывающие величины отклонений от точных значений. Пусть представляет собой точное значение, а и − среднее и дисперсию в наблюдениях, тогда при доверительной вероятности вычислим доверительный интервал как , где обозначает квантиль распределения Стьюдента с 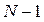степенями свободы. Результаты, приведенные на графике, показывают, что все доверительные интервалы содержат точное значение площади и становятся меньше с ростом продолжительности прогона. Этот факт характерен для имитационных моделей и должен учитываться в дополнение к известному выводу математической статистики − уменьшение доверительного интервала с ростом числа наблюдений.

Другим широко используемым способом понижения дисперсии является так называемый антитетический метод. В основе метода лежит очевидный факт, что если 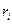случайное число, равномерно распределенное на интервале (0,1), то и 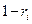обладает теми же свойствами. В соответствии с методом проводится два прогона модели с указанными случайными числами и находится их среднее арифметическое. Далее поступают указанным выше способом.

Приведенное здесь обсуждение показывает, что имитационное моделирование не сводится к разработке модели и составлению машинной программы, а представляет собой статистический эксперимент и его результаты необходимо рассматривать именно с этой точки зрения.

Задание по разделу: студент выбирает определенный интеграл (любой берущийся в элементарных функциях), находит его точное значение и проводит статистический анализ результатов по схеме приведенной выше. Результаты представляются в виде таблицы и графиков.

Дата добавления: 2015-07-25