Определение логических операций

Простейшей из логических операций является отрицание, с помощью которого из данного высказывания образуется противоречащее ему высказывание. В обычном языке операция выражается словами "неверно, что" или просто "не", в символическом – знаком отрицания, поставленным перед высказыванием. Если дано высказывание х, то его отрицание будет -x. В обычной речи отрицание чаще всего стоит перед глаголом и именной частью сказуемого. Например, отрицанием высказывания "2 есть четное число" будет высказывание "Неверно, что 2 есть четное число", которое ложно. Отрицая его, получим высказывание "Неверно, что 2 не есть четное число", которое равнозначно высказыванию "2 есть четное число". Это означает, что двойное отрицание приводит к первоначальному высказыванию. Обратите внимание, что высказывание, полученное путем отрицания первоначального, является противоречащим ему, т.е. оно отрицает нечто, но не утверждает что-то. Так, когда мы говорим, что "этот лист бумаги не белый", то не утверждаем, что он зеленый, синий или фиолетовый.

Для определения отрицания используется матрица (таблица) истинности, в которой в левой колонке даются два значения истинности ("истина" и "ложь") первоначального высказывания, а в правой колонке – его отрицания (табл.1). Истинность высказывания будет обозначаться буквой "и" или числом 1, ложь – буквой "л" и числом 0.

Если высказывание истинно, то противоречащее ему высказывание будет ложно, и, наоборот, если высказывание ложно, то противоречащее высказывание будет истинно.

Конъюнкция (логическое произведение) двух или нескольких простых высказываний образуется путем их объединения логической связкой "и". Например, если обозначить одно из простых высказываний буквой х, а другое – у, тогда их конъюнкцией будет сложное высказывание "х и у" или "х Ù у", где знаком Ù обозначен конъюнктивный оператор (логическая связка). Простые высказывания, входящие в сложное, называются конъюнктивными членами.

Конъюнкция будет считаться истинной, если и только если все ее конъюнктивные члены будут истинными. Наличие хотя бы одного ложного члена превращает всю конъюнкцию в ложное высказывание. Исходя из этого нетрудно построить таблицу истинности для конъюнкции (табл. 2).

Дизъюнкция (логическая сумма) двух или нескольких простых высказываний образуется путем объединения их логической связкой "или". Союз "или" в языке чаще всего употребляется в исключающем смысле, когда происходит выбор между двумя альтернативами: либо одно, либо другое. Реже используется этот союз в неисключающем смысле, т.е. выражается словом "а также". В логике и математике связка "или" употребляется преимущественно в неисключающем смысле. Так, например, дизъюнкция "2 меньше 3 или 3 меньше 5" понимается в неисключающем смысле, так как не только 2, но и 3 меньше 5.

Неисключающая дизъюнкция считается ложной в том и только в том случае, когда все ее дизъюнктивные члены будут ложными. Поэтому достаточно одного истинного члена, чтобы дизъюнкция была истинной. Исключающая дизъюнкция истинна тогда, когда только один из ее членов является истинным, а другой – ложным. Она будет ложной, если оба ее члена одновременно истинны либо ложны. Оператор дизъюнкции обозначается символом Ú – для неисключающей дизъюнкции и символом Ú – для исключающей дизъюнкции.

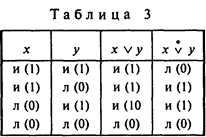
Учитывая принятые соглашения, мы можем построить таблицы истинности (табл. 3) для неисключающей (слева) и исключающей (справа) дизъюнкции.

Операция импликации состоит в образовании сложного высказывания из двух простых высказываний посредством логической связки, обозначаемой словами "если..., то... " и приблизительно соответствующей условному предложению в естественном языке. В логике эту связку называют импликацией, и мы будем обозначать ее стрелкой.

Условное высказывание состоит из двух простых высказываний. То из них, которое вводится словом "если", называется антецедентом (предыдущим высказыванием), а также основанием, а начинающееся словом "то" – консеквентом (последующим высказыванием) или следствием условного высказывания.

В науке и повседневном мышлении условные высказывания употребляются для установления связи между высказываниями, которые могут иметь различную форму. С помощью понятий антецедента и консеквента определяются необходимые и достаточные условия. Так, антецедент есть достаточное условие (основание) для консеквента (следствия). Например, в высказывании "Если треугольник имеет равные стороны, то и все его углы будут равны" условие равенства сторон служит достаточным условием (основанием) для следствия – равенства его углов. Одновременно с этим можно сказать, что следствие является необходимым условием для основания, так как "Равенство углов треугольника есть необходимое условие для равенства его сторон".

В обычной речи часто не проводят различия между основанием и следствием, как логическим отношением, и причиной и следствием, как отношением реального мира. Убедиться в наличии причинной связи можно лишь путем конкретного исследования явлений окружающего нас мира. Если одно явление вызывает или порождает другое явление, то первое из них мы называем причиной, а второе – следствием. Так, нагревание стержня – причина – вызывает его удлинение – следствие. Эту зависимость мы устанавливаем эмпирически – путем наблюдения и измерения. Логическое отношение между основанием и следствием не нуждается в эмпирическом исследовании, так как устанавливается с помощью чисто логических рассуждений. В нашем примере равенство углов равностороннего треугольника выводится как геометрическая теорема.

Условные высказывания употребляются для выражения самых разнообразных отношений между высказываниями, но не во всех случаях при этом учитывается их содержание и смысл. В современной логике обращается внимание исключительно на связь между высказываниями по значению их истинности, потому что задача логики состоит в том, чтобы гарантировать истинность заключения из истинных посылок, а для этого необходимо перенести истинность с посылок на заключение. В связи с этим в логической импликации абстрагируются (отвлекаются) от содержания и смысла и обращают внимание только на связь высказываний по значению их истинности. В результате можно рассматривать импликации, которые выглядят бессмысленными и парадоксальными с точки зрения обычного, здравого смысла. Например, "Если 2 х 2 = 5, то Москва – большой город" считается не только допустимой, но и истинной импликацией.

Дата добавления: 2015-07-25