Таким образом, импликация учитывает все случаи распределения значений истинности и считается ложной только тогда, когда ее антецедент истинен, а консеквент ложен.

Например, импликация "Если 2 х 2 = 4, то Москва – небольшой город" является ложной, так как ее антецедент – истинное высказывание, а консеквент – ложное.

Отсюда ясно, что импликация выражает важнейшее свойство правильных рассуждений. Известно, что из истинных посылок нельзя получить ложное заключение, если рассуждать правильно. Этот фундаментальный принцип лежит в основе всей дедуктивной логики и сохраняется при определении операции импликации.

Распределение значений истинности высказываний для импликации представлено табл.4, где стрелка обозначает импликацию.

Резкое расхождение между употреблением условных высказываний в естественной речи и современной логике породило немало споров и дискуссий, в которых логиков обвиняли в том, что они не учитывают смысловой связи между высказываниями, и поэтому приходят к бессмыслице. Но как уже подчеркивалось выше, логики рассматривают условное высказывание только как импликации, т.е. с точки зрения значений истинности антецедента и консеквента. Импликация является операцией формализованного языка, а не конкретным условным высказыванием, которое может пониматься по-разному в различных контекстах (причинная связь, отношение между достаточными и необходимыми условиями, связь основания и следствия и т.п.). Когда не учитывается различие между формализованным и естественным языком, междуимпликативным и условным высказываниями, тогда неизбежно возникают п а р а д о к с ы импликации, наиболее известные из которых связаны с отождествлением импликации с логическим следованием. Тот факт, что в импликации истинный консеквент получается из любого антецедента – истинного и ложного, стали истолковывать как утверждение, что истина с л е д у е т и зч е г о у г о д н о. Или другими словами, что ложный антецедент имплицирует любой – истинный или ложный – консеквент, начали интерпретировать как утверждение, что из ложного высказывания следует любое высказывание. Но эти утверждения не согласуются с нашими интуитивными представлениями, и поэтому выступают как парадоксы так называемой материальной импликации. В последние десятилетия были предприняты усилия по преодолению этих парадоксов и поиску таких логических понятий, которые более адекватно отразили бы смысловую связь в условных высказываниях. Весь вопрос, однако, состоит в том, как выявить такую связь в общем виде, независимо от конкретного содержания антецедента и консеквента. Во всяком случае импликации, претендующие на отображение смысла, будут заведомо более узкими, чем понятие материальной импликации.

Операция эквивалентности объединяет два высказывания, имеющие одинаковые значения истинности. Следовательно, будут эквивалентными, с одной стороны, истинные высказывания, а с другой – высказывания ложные. В противном случае высказывания считаются не эквивалентными. Исходя из этого легко построить таблицу истинности для эквивалентности, символом которой служит стрелка с противоположными концами (табл. 5).

Эквивалентность можно выразить на естественном языке словами "если и только если", и в таком виде она часто встречается в формулировке научных определений.

Кроме табличного определения логические операции (за исключением отрицания) можно определить через другие, с обязательным использованием отрицания. Действительно, применив табличный метод (табл. 6), можно убедиться, что выражения (х→у) и (y → x) будут эквивалентными, т.е. (х→у) ↔ (у→x).

Каждая строка первой импликации и второй конверсной (обратной), полученной перестановкой отрицаний консеквента и антецедента первой, совпадают друг с другом. Следовательно указанные импликации будут эквивалентны.

С помощью таблиц истинности можно проверить, что и остальные логические операции можно определить через Другие две, причем второй операцией всегда будет отрицание. Например, дизъюнкцию можно выразить через конъюнкцию: (х Ú у) ↔ (x Ù y).

Способ установления истинности сложных высказываний, образованных из простых с помощью таблицы, был предложен американским логиком Ч.С. Пирсом и оказался весьма удобным. Как мы видели, этот способ основывается на комбинации значений истинности простых высказываний и последующего определения истинности сложных высказываний, образованных с помощью операций отрицания, конъюнкции, дизъюнкции и импликации. Например, когда имеется два высказывания, то число различных комбинаций из их значений истинности будет равно 4, при трех – 8, при четырех – 16, а следовательно, при заданном числе п оно равно 2ⁿ. Отсюда нетрудно заметить, что определение истинности сложного высказывания сводится в сущности к вычислению ее на основе значений истинности простых высказываний. Это впечатление усилится, если мы обозначим истину как 1, а ложь как 0 и будем их комбинировать, чтобы образовать отрицание, конъюнкцию, дизъюнкцию и т.д. В качестве иллюстрации вычислим значение истинности следующего выражения: (х Ú y) → (x Ù z).

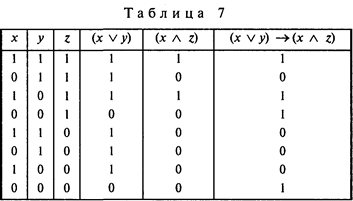
При некотором навыке процесс вычисления можно ускорить, обратив главное внимание на основную операцию, которая связывает две части формулы. В приведенном примере (табл. 7) достаточно заметить, что ложная импликация возникает при истинном антецеденте и ложном консеквенте. Отсюда легко определить возможные значения х и у в дизъюнкции (х Ú у), а также значения х и z в конъюнкции (х Ù z). Такой сокращенный способ вычисления истинности сложного высказывания основывается на установлении главной логической операции в рассматриваемой формуле.

Дата добавления: 2015-07-25