|
Читайте также: |
ВАРИАНТ ДЛЯ САМОПОДГОТОВКИ
1. Найдите матрицу 
из уравнения 
.
2. Найдите точку пересечения прямой, проходящей через точки 
и 
, с
плоскостью, проходящей через точки 
, 
и 
.
3. В условиях задачи 2 вычислите векторное произведение векторов 
и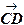 
. и смешанное
произведение векторов 
, и .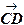
4. Для матрицы 
вычислите матрицу 
и подсчитайте 
, где 
угол между
линейно независимыми собственными векторами матрицы 
.
5. Для матрицы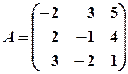 
найдите обратную матрицу 
и сделайте проверку.
6. Решите систему линейных уравнений 
а) для случая 
; б) в общем случае; в) найдите наименьшее по длине решение.
7. Найдите величину угла между векторами 
и 
,
если матрица Грама базиса 
равна 
.
8. В условияхпредыдущей задачи найдите площадь треугольника, построенного на векторах 
, и объем тетраэдра, построенного на базисных векторах.
9. В базисе из задачи 7 линейный оператор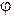 
имеет матрицу 
,
а вектор 
. Найдите матрицу сопряженного оператора 
в том же базисе и
вычислите координаты векторов 
и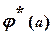 
в базисе .
10. В некотором ортонормированном базисе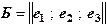 
линейный оператор 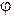имеет матрицу
.Найдите ортонормированный базис, в котором матрица оператора диагональна.
11. В условиях задачи 10 представьте вектор 
в виде суммы двух собственных
векторов оператора .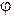
12. В параллелепипеде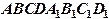 
заданы координаты четырех вершин: 
. Найдите координаты точки 
. Вычислите площадь треугольника 
и объем параллелепипеда.
13. В условиях задачи 12 найдите расстояние от точки 
до прямой 
, координаты проекции
точки на прямую и координаты точки, симметричной точке относительно прямой .
14. В условиях задачи 12 найдите расстояние от точки до плоскости 
, вычислите
координаты вектора, являющегося проекцией вектора 
на плоскость , и найдите
величину угла между прямой 
и плоскостью .
15. В условиях задачи 12 найдите величину угла между плоскостями и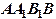 
.
16. В условиях задачи 12 напишите формулы перехода от базиса 
к новому базису. 
.
17. Линейный оператор 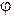является оператором проектирования векторов трехмерного пространства на плоскость из задачи 12. Найдите матрицу этого оператора в базисе 
, укажите собственные числа и собственные векторы этого оператора. Выясните, является ли этот оператор самосопряженным. Проверьте равенство 
для любого вектора 
.
18. Линейный оператор 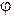в базисе 
(здесь 
) имеет матрицу 
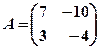.Найдите матрицу этого оператора в базисе 
(здесь 
),
19. Укажите базис 
, в котором матрица оператора из задачи 18 диагональна.
20. Квадратичная форма задается формулой 
, где 
суть координаты вектора 
в базисе из задачи 18. Найдите матрицу этой квадратичной формы в базисе из задачи 18.
21. Приведите квадратичную форму из задачи 20 к диагональному виду.
22. Укажите, при каких значениях параметра p квадратичная форма 
а) положительно определена,
б) отрицательно определена.
23. Найдите базис в линейной оболочке 
пяти векторов пространства 
.
и разложите каждый из этих векторов по выбранному Вами базису.
24. Опишите процедуру построения матрицы линейного оператора в заданных базисах.
Дата добавления: 2015-07-25; просмотров: 62 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Словарь биохимических терминов | | | Химическая связь и строение вещества |