Профессор Синяков Г.Н.

Кафедра физико-математических дисциплин

Расчётная работа

«Закон Максвелла раcпределения молекул по скоростям»

Вариант № 25

Выполнил студент группы

№ 181012 Костров Р.М.

Проверил преподаватель

Профессор Синяков Г.Н.

Примечание Номер варианта соответствует порядковому номеру фамилии студента в списке группы.

Программу можно скачать по ссылке:

Ссылка на math_cad http://rutracker.org/forum/viewtopic.php?t=1798874

Цель работы. Анализ функции распределения молекул по скоростям в зависимости от температуры и молярной массы газа.

Теория

При изучении газов принята основная модель –модель идеального газа как большого коллектива невзаимодействующих частиц, непрерывно участвующих в беспорядочном тепловом движении. К этому коллективу частиц применим статический метод, базирующийся на математической теории вероятностей, на понятиях о средних, среднеквадратичных и наиболее вероятных параметров, характеризующих поведение частиц в коллективе.

Рассмотрим распределение Максвелла или распределение молекул по скоростям.

Скорости молекул газа имеют различные значения и направления, причем как величина, так и направление скорости каждой отдельной молекулы изменяются в результате соударений, поэтому нельзя определить число молекул, обладающих точно заданной скоростью в данный момент времени, но можно подсчитать число молекул, скорости которых лежат в интервале от v₁ до v₂.

При этом предполагалось, что в газе не существует молекул, имеющих в точности одинаковые скорости, и число молекул d N, скорость которых лежит в узком интервале между v и v + d v, пропорционально общему числу молекул N, ширине интервала d v и зависит от скорости v. Такая теоретическая зависимость была установлена Максвеллом на основании теории вероятностей:

d N(v) = 4π (1)

Функцию

f (v) = = 4π (2)

показывающую относительное число молекул, скорость которых лежит в интервале скоростей, называют функцией распределения молекул. В этой формуле: m - масса молекул, k – постоянная Больцмана, Т – абсолютная температура. Используя соотношение между постоянной Больцмана k и универсальной газовой постоянной R=kN_A, формулу (2) можно переписать в виде:

f (v) = 4π (3)

где M – молярная масса газа. Эта функция удовлетворяет условию нормировки:

(3*)

Максимум кривой распределения соответствует наиболее вероятной скорости молекул v _B, которую можно найти, исследовав на максимум функцию f (v). Беря производную от функции (2) по скорости и приравнивая ее нулю, получаем

= const =0, =0

откуда

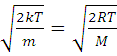= , (4)

Вид функции распределения f (v) зависит от рода газа (массы молекул) и температуры Т. Давление и объем газа на распределение молекул по скоростям не влияют.

При повышении температуры (T₂>T₁) v _B, возрастает, поэтому максимумы кривой распределения молекул по скоростям сдвигаются в сторону больших скоростей (v₂>v₁); следовательно, с ростом температуры возрастает относительное число молекул, обладающих большой скоростью. Площади, ограниченные кривыми распределения при любых температурах, должны быть равны между собой, так как их величина пропорциональна общему числу молекул, которое в обоих случаях сохраняются неизменным.

Большинство молекул газа движется с наиболее вероятной скоростью, тогда как число молекул, имеющих очень малые и очень большие скорости, мало. Кроме наиболее вероятной скорости движение молекул газа характеризует:

· средняя арифметическая скорость , определяемая формулой .

Для дискретных значений v из общего определения средней арифметической скорости имеем

=

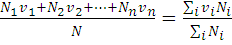
[ N - число частиц. имеющих скорость v_i ].

В случае непрерывного спектра значений скорости

.

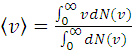Однако полное число частиц N = ; следовательно,

= .

Подставляя в (4) f (v) и интегрируя полученное выражение, находим

= , (5)

· средняя квадратичная скорость

= , (6)

равна корню квадратному из среднего арифметического значения квадратов скоростей.

если все молекулы одинаковы по массе, то

v _B < < .

Функцию распределения по скоростям можно записать в другом виде, введя понятие относительной скорости 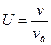. Проведя математические преобразования формулы (2), получим выражение

, (7)

где - доля молекул, обладающих относительными скоростями в интервале от U до U + ΔU, ΔU =

Порядок выполнения работы

Функция распределения рассчитана с помощью математического метода MathCad. Исследуемые соединения и их характеристики представлены в Таблице 1.

Таблица 1

№	Соединение	Химическая формула	Молярная масса (10^-3кг/моль)	Пределы изменения температуры (для пункта 2)
	гелий	He		273-450
	метан	CH3		300-500
	кислород	O2		220-400
	пары воды	H2 O		373-500
	неон	Ne		273-500
	пары метанола	CH3OH		370-500
	углекислый газ	CO2		263-450
	этан	C2H5		300-500
	азот	N2		273-400
	воздух			220-450
	закись азота	N2 O		283-500
	аргон	Ar		300-500
	бутан	C3H8		250-450
	пары этанола	C2H5 OH		363-400
	сернистый газ	SO2		250-500
	хлор	Cl2		273-400
	пары диэтилового эфира	C2H5 O C2H5		365-450
	ксенон	Xe		300-500
	пары йода	I2		323-520

Каждый студент, выполняющий работу, рассчитывает характеристики определённого набора соединений. Номера соединений указаны в Таблице 2. Номер варианта соответствует порядковому номеру фамилии студента в списке группы.

Таблица 2.

№ варианта	Соеденения	№ варианта	Соеденения
	1 6 9 11 16 18		9 10 11 14 18 19
	2 7 8 12 17 14		5 11 14 15 16 17
	3 8 13 18 15 5		2 4 7 10 18 19
	4 9 14 19 1 11		3 8 9 15 2 14
	5 10 15 18 2 12		1 3 4 6 12 18
	3 1 5 7 9 11		4 8 9 12 16 18
	2 4 6 13 15 17		6 7 11 12 13 14
	5 7 9 11 16 18		3 8 11 15 16 12
	4 8 12 18 16 5		2 6 12 13 15 16
	3 9 12 15 13 7		3 7 8 10 13 19
	5 7 11 16 15 9		1 8 9 11 15 16
	10 2 3 4 5 11		2 7 8 15 16 17
	3 4 6 8 15 18		3 6 7 10 11 18
	5 9 14 17 1 14		4 7 10 12 15 16
	1 3 7 12 13 19		5 9 11 13 17 19
	5 6 9 13 17 18		1 2 7 10 11 12

---

Дата добавления: 2015-07-25