Читайте также:
|
Определение. Точка 
называется нулем аналитической функции 
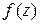порядка (или кратности) 
, если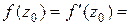 
. В случае 
точка называется простым нулем.
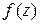Теорема. Для того, чтобы точка была нулем -гo порядка функции , аналитической в точке , необходимо и достаточно, чтобы в некоторой окрестности этой точки имело место равенство 
, где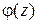 
аналитична в точке и 
.
Пример 1. Найти нули функции 
и определить их порядки.
Из уравнения 
находим точки 
, 
– нули данной функции. Имеем: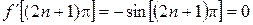 
, 
, т.е. точки 
– нули второго порядка данной функции.
Пример 2. Найти нули функции 
и определить их порядки.
Полагая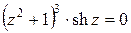 
, получаем, что 
или 
. Решая эти уравнения, находим нули функции 
. Пусть 
; тогда 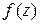можно представить в виде 
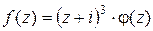, где функция 
является аналитическойв точке , причем 
. Это означает, что точка есть нуль третьего порядка.Аналогично доказывается, что и точка 
является нулем третьего порядка. Исследуем нули 
. Производная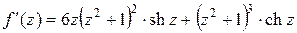 
в точках отлична от нуля. Следовательно, – простые нули функции .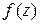
Дата добавления: 2015-07-25; просмотров: 69 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Допоміжна | | | Изолированные особые точки |