Сложные учетные ставки

При антисипативном способе начисления сложных процентов (проценты начисляются в начале каждого интервала), формула наращенной суммы имеет вид:

,

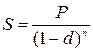где S – сумма, которая должна быть возвращена; P – сумма получаемая заемщиком; d – величина сложной учетной ставки; n – количество лет.

Для периода начисления, не являющегося целым числом, наращенная сумма будет определяться:

,

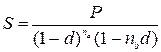где – n_a – целое число лет; n_b – оставшаяся дробная часть года.

При учетной ставке, изменяющейся в течение срока ссуды, наращенная сумма определяется:

,

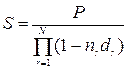где n₁, n₂,…,n_N – продолжительность интервалов начисления в годах; d₁, d₂,...,d_N – годовые учетные ставки, соответствующие данным интервалам; N – количество интервалов начисления сложных процентов.

Если проценты начисляются m раз в году, наращенная сумма определяется:

,

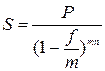где f – номинальная годовая учетная ставка; mn – общее количество интервалов начисления.

Если общее число интервалов начисления не является целым числом, то наращенная сумма будет определяться:

,

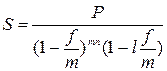где mn – целое число интервалов начисления за весь период начисления; l – часть интервала начисления.

Пример

Определить современное значение суммы в 100.000.000 рублей, которая будет выплачена через 2 года при использовании учетной ставки 20% годовых.

Дата добавления: 2015-07-25