Сложные ставки ссудных процентов

Если после очередного интервала начисления доход не выплачивается, а капитализируется, то для определения наращенной суммы применяются формулы сложных процентов. Сложные ссудные проценты достаточно широко применяются на практике.

Чем больше период начисления, тем больше разница в величине наращенной суммы при начислении простых и сложных процентов.

Формула для расчета сложных процентов имеет вид:

,

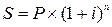где S – наращенная сумма; P – величина первоначальной денежной суммы; n – продолжительность периода начисления в годах; i – ставка сложных ссудных процентов; n – количество лет.

Если срок ссуды не является целым числом, то формула для расчет наращенной суммы определяется:

,

где n_а – целое число лет; n_b – оставшаяся дробная часть года.

В случае если уровень сложных процентных ставок различается на разных интервалах начисления, то в конце всего периода начисления наращенная сумма будет определяться:

,

где n₁, n₂,…,n_N – продолжительность интервалов начисления в годах; i₁, i₂,...,i_N – годовые ставки процентов, соответствующие данным интервалам; N – количество интервалов начисления сложных процентов.

Если все интервалы начисления одинаковы (как обычно бывает на практике) и ставка сложных процентов одна и та же, то наращенная сумма будет определяться:

Начисление сложных процентов может осуществляться несколько раз в году, в этом случае оговаривается номинальная ставка процентов (j), то есть годовая ставка, по которой определяется величина ставки процентов, применяемая на каждом интервале начисления.

При m равных интервалах начисления и номинальной процентной ставке (j), величина номинальной процентной ставки, применяемой на каждом интервале начисления определяется .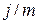

Если срок ссуды составляет n лет, то наращенная сумма будет определяться:

,

где j – номинальная ставка сложных ссудных процентов; mn – общее число интервалов начисления за весь срок ссуды.

Если общее число интервалов начисления не является целым числом, то наращенная сумма будет определяться:

,

где l – часть интервала начисления.

Дата добавления: 2015-07-25