Алтарное окно

Я провел несколько экспериментов со многими испытуемыми по решению следующей задачи. Некоторые дети проявляли себя очень хорошо и иногда находили решение после всего лишь минутного обдумывания; другим требовалась незначительная помощь. Однако некоторые, даже весьма умные и образованные взрослые, действовали довольно странно и, пытаясь найти простое решение, испытывали большие затруднения.

Я предлагаю читателю попытаться решить эту задачу.

Художники заняты окраской и отделкой внутренних стен церкви. Немного выше алтаря находится круглое ок­но. В декоративных целях художников попросили прове­сти две вертикальные линии, касательные к кругу и такой же высоты, что и круглое окно;

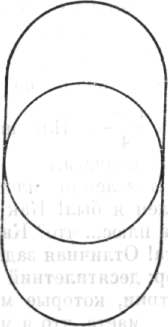
Рис. 170

затем они должны были прибавить снизу и сверху полу­круги, замыкающие фигуру. Эта поверхность между ли-

ниями и окном должна была покрываться золотом. На каждый квадратный дюйм требуется столько-то золота. Сколько потребуется золота для покрытия этой поверхно­сти (при заданном диаметре окна) или чему равна пло­щадь между окном и линиями?

Прежде чем продолжить чтение, попытайтесь найти решение. (Для этого вам не потребуются глубокие знания математики.) Решив задачу, возможно, вы с интересом узнаете об ответах, которые мы получили в экспериментах с этой задачей. Расскажу лишь о некоторых из них. Воз­можно, они доставят вам удовольствие.

Вот, например, слова одного высокообразованного ис­пытуемого: «Конечно, я должен решить ее. Посмотрим... какие теоремы об определении площадей необходимы в данном случае? Несомненно, я должен вспомнить их... Если бы только это был настоящий эллипс (пауза)... но это не эллипс... Если я разделю его, то площади этих час­тей будет легко определить. Внизу и вверху у нас полу­круги, а площадь полукругов я могу легко вычислить. Но есть еще эти четыре забавных кусочка... Какие теоремы я знаю о таких «квазитреугольниках», у которых вместо прямой стороны такой круговой сегмент?.. Не помню ни одной...» И затем после глубокого раздумья он сдался.

Другой испытуемый, столь же сообразительный и с хо­рошей подготовкой по геометрии, действовал аналогичным образом. Но, дойдя до четырех остатков странной формы, он сказал: «Площадь этих четырех фигур равна площади квадрата минус площадь круга, вписанного в квадрат... Площадь

каждого из остатков равна	, это равняется а ^2, умноженное на …
Или не так?.. Правильно? (На это потребовалось полчаса.)

Третий начал с вычисления площади круга и вдруг воскликнул: «Как слеп я был! Как это просто! Площадь равна площади круга плюс... что? Квадрат... круг; это про­сто площадь квадрата! Отличная задача!»

Четвертый пример: десятилетний ребенок без каких-ли­бо знаний по геометрии, которые могли бы ему помочь, сказал: «Почему вы думаете, что я могу сделать это? Я не могу. Не имею ни малейшего представления, как делаются подобные вещи». Он внимательно посмотрел на рисунок, а затем спокойно сказал: «Два полукруга должны войти в «окно... Это полный квадрат». (Он не пользовался термином

«квадрат», а провел по рисунку пальцем.) На все это ушло около минуты.

Пятый: еще один мальчик, двенадцати лет, без какой-либо подготовки по геометрии, начал хвастать тем, как легко он решает такие задачи, и с большой уверенностью высказывал самые дикие предположения. Например: «Че­тыре остатка составляют четверть круга». Я сказал ему: «Не говори чепухи. Подумай немного». Он полминуты мол­чал и затем сказал: «Если вы передвинете два верхних остатка наверх и вставите их в верхний полукруг и если вы проделаете то же самое с нижними остатками, то обе части в совокупности составят квадрат! Вот так».

ПРИЛОЖЕНИЕ 3

Дата добавления: 2015-07-25