Примеры 3 страница

Наблюдались реакции различных типов.

Первый тип. Вообще никакой реакции.

Или кто-нибудь говорил: «Фу! Математика!» — и от­казывался решать задачу со словами: «Не люблю матема­тику».

Некоторые испытуемые просто вежливо ждали или спрашивали: «Что же дальше?»

Другие говорили: «Не знаю; этому меня не учили». Или: «Я проходил это в школе, но совершенно забыл», и все. Некоторые выражали недовольство: «Почему вы считаете, что я смогу это сделать?» И я отвечал им: «А почему бы не попробовать?»

Второй тип. Другие энергично рылись в памяти, пы­таясь вспомнить что-нибудь такое, что могло бы им по­мочь. Они слепо искали какие-нибудь обрывки знаний, ко­торые могли бы применить.

Некоторые спрашивали: «Можно спросить у моего старшего брата? Он наверняка знает». Или: «Можно по­смотреть ответ в учебнике геометрии?» Очевидно, это то­же является одним из способов решения задач.

Третий тип. Некоторые начинали пространно рассуж­дать. Они вели разговор вокруг задачи, рассказывая об аналогичных ситуациях. Или же классифицировали ее ка­ким-то образом, применяли общие понятия, относили за­дачу к какой-то категории или осуществляли бесцельные пробы.

Четвертый тип. Однако в ряде случаев можно было наблюдать реальный процесс мышления — судя по черте­жам, замечаниям, мыслям вслух.

1) «Вот эта фигура; как я могу определить величину площади? Площадь фигуры именно этой формы?»

2) «Что-то нужно сделать. Я должен что-то изменить, изменить таким образом, чтобы это помогло мне ясно уви-

деть площадь. Что-то здесь не так». На этом этапе неко­торые из детей чертили фигуру, показанную на рис. 21.

Рис. 21

В таких случаях я говорил: «Хорошо было бы сравнить величину площади параллелограмма с площадью прямо­угольника». Ребенок беспомощно прекращал, а затем во­зобновлял попытки.

В других случаях ребенок говорил: «Я должен изба­виться от затруднения. Эту фигуру нельзя разделить на маленькие квадраты».

Рис. 22

3) Здесь один ребенок неожиданно сказал: «Можете дать мне складной метр?» Я принес ему такой метр. Ре­бенок сделал из него параллелограмм, а затем превратил его в прямоугольник.

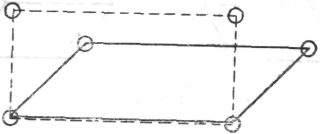
Рис. 23

Мне это понравилось. «Ты уверен, что это правиль­но?» — спросил я. «Уверен», — ответил он. Только с боль­шим трудом с помощью соответствующего чертежа

(рис.24) мне удалось заставить его усомниться в пра­вильности его метода.

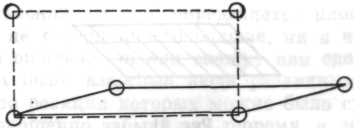
Рис. 24

Тут он сразу сказал: «Площадь прямоугольника го­раздо больше — этот метод не годится...»

4) Ребенок взял лист бумаги и вырезал из него два равных параллелограмма. Затем со счастливым видом со­единил их следующим образом.

Рис. 25

Но он не знал, что предпринять дальше.

Сам по себе этот шаг был прекрасной находкой (ср. решение с кольцом, с. 78). Замечу, что в ряде случаев я сам давал детям два образца фигуры. Иногда я сталкивался с такими реакциями:

Рис. 26

Некоторые дети даже пытались наложить одну фигу­ру на другую. Такая помощь могла быть эффективной только при некоторых условиях. При каких же именно?

31. Но были случаи, когда мышление вело прямо к цели. Некоторые дети с незначительной помощью или во­обще без всякой помощи находили правильное, разумное, прямое решение задачи. Иногда после периода крайней

сосредоточенности в критический момент их лица свет­лели. Какое чудо — этот переход от слепоты к прозрению, к пониманию сути дела!

Сначала я расскажу о том, что произошло с девочкой пяти с половиной лет, которой я вообще не оказывал ни­какой помощи при решении задачи с параллелограммом. Когда после короткой демонстрации способа определения площади прямоугольника ей предложили задачу с парал­лелограммом, она сказала: «Я, конечно, не знаю, как это сделать». Потом, после минуты молчания, добавила: «Не­хорошо здесь, — и показала на область, расположенную

Рис. 27

справа, — и здесь тоже, — и показала на область, располо­женную слева. — Трудность связана с этим местом и с этим». Нерешительно сказала: «Здесь я могут исправить... но...» Вдруг она воскликнула: «Можете дать мне ножни­цы? То, что мешает там, как раз требуется здесь. Подхо­дит». Она взяла ножницы, разрезала фигуру вертикально и перенесла левую часть направо.

Другой ребенок аналогичным образом отрезал тре­угольник.

Рис. 28А	Рис. 28Б
В некоторых случаях действия были такими:
1) «Нарушение» 2) «Здесь слишком много» _________________ 3)	«Тоже нарушение» «Здесь слишком много»     «Нет! Здесь справа тре­буется именно то, что яв­ляется лишним слева»

И она приводила левый угол «в порядок». Затем, глядя на другой край, она попыталась сделать там то же самое, но внезапно стала рассматривать его не как «лишнюю часты», а как «недостающую».

Рис. 29

Встречались и другие действия. Девочка, которой я дал вырезанный из бумаги длинный параллелограмм (и в предыдущих примерах лучше начинать с длинного парал­лелограмма), вначале сказала: «Вся средняя часть в по­рядке, но края...» Она продолжала разглядывать фигуру, явно интересуясь ее краями, потом вдруг взяла ее в руки и с улыбкой превратила в кольцо, соединив края. Когда ее спросили, зачем она это сделала, она, удерживая свои­ми маленькими пальчиками сомкнутые края, ответила: «Но ведь теперь я могу разрезать фигуру вот так, - и указала на вертикальную линию, расположенную где-то посередине, — тогда все будет в порядке».

Наблюдались и несколько иные действия, но я не встречал ничего подобного тому, что предлагается в со­временных курсах математики — уменьшение нарушения посредством разрезания на горизонтальные ряды с высотой меньшей любого заданного бесконечно малого числа. Даже взрослые часто понимают эту процедуру с трудом. Операция разрезания на ряды со все меньшей в меньшей высотой, предложенная детям лет двенадцати и взрослым, вызывала у них забавные реакции. Считая та­кой способ «нечестным», некоторые продолжали ломать голову даже после того, как им показали, что после со­ответствующего горизонтального сдвига рядов вся фигура становится все больше и больше «похожей» на прямо­угольник. Эта процедура предполагает переход к понятию бесконечно малой величины и к операции предельного перехода. К этому методу пришли только после длительного развития математики, видимо, в связи с задачами на определение площади криволинейных фигур.

32. Какие же операции и шаги использовались в этой процедуре?

Мы видели, что в действительно продуктивных про­цессах, примеры которых мы только что привели, снова встречаются факторы, аналогичные тем, которые упомина­лись при обсуждении задачи на определение площади прямоугольника: перегруппировка частей целого, реорга­низация, операция согласования частей; в ходе решения испытуемые обнаруживают факторы внутренней связи, понимают, в чем заключаются внутренние требования за­дачи, а затем следуют этим требованиям. Последователь­ность этапов решения и осуществляющихся операций бы­ла обусловлена видением целостной фигуры и всей си­туации в целом. Они не были результатом слепого при­поминания или слепых проб; их содержание, направление я применение определялись требованиями проблемной си­туации. Такой процесс не является простой суммой от­дельных шагов, совокупностью не связанных друг с дру­гом операций, а представляет собой единый процесс мыш­ления, порождаемый осознанием пробелов в ситуации, же­ланием их исправить, выправить то, что плохо, достигнуть внутренней гармонии ¹. В ходе такого процесса мы исходим не от отдельных элементов с тем, чтобы затем перейти к их совокупности, движемся не «снизу вверх», а «сверху вниз», начиная с постижения сущности структурного на­рушения и переходя к осуществлению конкретных ша­гов.

Как мы видели, в хороших примерах не встречаются слепые пробы и ошибки. А если и встречаются, то от них быстро отказываются. Я не сталкивался в таких процессах с действительно нелепыми, слепыми операциями. Так, не

¹ Вначале мы не знаем, как определить площадь параллело­грамма. Мы хотим восполнить этот пробел, понять, каким именно образом величина площади определяется структурой фигуры. В случае задачи на определение площади длинного параллелограм­ма легко прийти к первому шагу: совершенно ясно, как опреде­лить площадь средней части параллелограмма — как и в случае прямоугольника; края же оказываются областями нарушения, ко­торые затем «также приводятся в порядок».

Эта операция осуществляется в результате осознания необхо­димости ликвидировать еще одну «брешь» в нашем понимании внутренней связи формы фигуры и площади: теперь один из краев следует рассматривать не как мешающий, лишний, который, не­обходимо отрезать, а как часть, которую нужно добавить к друго­му краю с тем, чтобы фигура превратилась в прямоугольник.

Рис. 30А Рис. 30Б

Не было вовсе таких случаев, когда бы трудности связы­вались с областями всех четырех углов, рассматриваемы­ми изолированно (рис. 30Б).

33. Можно, конечно, усвоить внешние признаки ре­шения и даже само решение в результате бессмысленных упражнений. Давайте прямо и честно рассмотрим, что же это значит с общетеоретической точки зрения.

Возьмем крайний случай. Можно «научить» нужным действиям, даже не формулируя задачу. Учитель делает построения. Ученики раз двадцать повторяют: «Одна вспо­могательная линия», и таким образом в результате мно­гократного подкрепления устанавливается новая связь. Затем они точно так же поступают со второй вспомога-

Рис. 31

тельной линией, «связывая» ее с фигурой, и т. д., и таким образом достигают цели, окончательного результата. Та­кая процедура по крайней мере вполне возможна, соглас­но ассоциативной теории. Я сам не проводил таких экспе-

риментов. Однако думаю, что даже достигнутый таким образом положительный результат будет сильно отличать­ся от хороших случаев с точки зрения их последствий, например в отношении забывания или применения.

Конечно, эти замечания с теоретической точки зрения являются крайне упрощенными. Всестороннее исследова­ние должно включать обсуждение всех дополнительных гипотез, выдвинутых в рамках ассоциативного подхода, пытавшегося свести все разумные процессы к совокупно­сти механических, слепых связей. Все вышесказанное можно рассматривать лишь как намек на содержащуюся здесь фундаментальную проблему.

34. Выше уже отмечалось, что иногда ученик концен­трирует свое внимание на левом крае параллелограмма и устраняет нарушение, отрезая лишнее, затем переходит к правому краю, где находится область, которую необходи­мо заполнить. В результате ликвидируется нарушение справа и используется часть, которая была лишней слева.

Такое описание последовательности действий, по-ви­димому, не является адекватным отражением того, что происходит в других случаях, когда испытуемый рассмат­ривает одновременно обе области нарушений, то есть устраняет нарушения на обоих краях, воспринимая фигу­ру в целом: то, что является лишним слева, используется как то, что необходимо справа. Оба действия выполня­ются вместе и требуют одно другого.

Это еще более отчетливо проявляется в решении с кольцом: оба края рассматриваются как соответствующие друг другу; для устранения нарушений их необходимо соединить. Между ними нет функционального различия,

оба края в равной степени являются нарушениями, кото­рые одновременно устраняются в результате взаимной компенсации.

Решение посредством разрезания фигуры посередине и перемещения частей часто очень похоже на это:

получите необходимые прямоугольные края, вертикально разрезая в каком-нибудь месте фигуру; устраните мешающие края, соединив их вместе (сдвиг).

Тот, кто почувствовал своеобразие таких решений, поймет, что наибольшую опасность для развития таких удиви­тельных процессов представляет прежде всего слепое вспоминание, слепое применение чего-то заученного, ста­рательное выполнение отдельных операций, неспособность увидеть всю ситуацию в целом, понять ее структуру и ее структурные требования. Хотя у меня нет достаточных количественных данных на этот счет, мне кажется, что способность продуцировать творческие процессы часто значительно уменьшается, когда школьники привыкают к механическому заучиванию.

На рисунках показано направление векторов в ходе такого процесса. Кратко существенные черты динамики такого процесса мышления состоят в следующем: столк­новение с проблемой; нахождение векторов, которые свя­заны со структурными особенностями ситуации и опре­деляются ими, неясность, незавершенность ситуации, тен­денция к конкретизации областей нарушения и тенденция к осуществлению операций по изменению. Ни положение, ни направление векторов не является случайным. Все используемое, независимо от того, вычленено ли оно из данной ситуации или извлечено из памяти, включается

в процесс благодаря тому, что выполняет определенную структурно необходимую функцию, превращает исходную» ситуацию с ее неясностями в четкую, завершенную ко­нечную ситуацию; этот процесс представляет собой пере­ход от плохого гештальта к хорошему.

Мое описание этого процесса кажется очень сложным потому, что я описывал его фазы по отдельности и после­довательно, а также потому, что я пользовался формаль­ными терминами, чуждыми традиционным подходам. Но разве это описание выглядит столь сложным, напри­мер, в случае кольца, где вся суть процедуры заключа­ется просто в том, что наклонные стороны, которые яв­ляются нарушениями, в результате замыкания фигуры перестают быть боковыми сторонами и исчезают как та­ковые? Замыкание ликвидировало нарушения, и теперь фигура воспринимается как обычная, горизонтально и вертикально ориентированная полоса, которая, будучи разрезанной вертикально, является прямоугольником. Тер­мины вроде «функция части в целом», «изменение функ­ции», «изменение отдельных элементов» необходимы для точности формулировки, но они не должны скрывать от нас простой, понятный характер такого процесса.

35. Я не буду здесь затруднять читателя подробным структурным анализом таких процессов. Я дам только некоторое представление о структуре таких процессов.

Если в ходе таких процессов проводятся три вспомога­тельные линии, то они появляются не как «перпендику­ляр, опущенный из левого верхнего угла, и перпендику­ляр, опущенный из правого верхнего угла, и продолже­ние основания за правую вершину», которые, возможно, позднее и приобретут какой-то смысл, какое-то значение. Их появление обусловлено функциональными требования­ми, той ролью, которую они выполняют как части фигу­ры. И в этом процессе части фигуры меняют свое функ­циональное значение:

1) Дополнительная линия слева возникает:

(а) как правильно проведенная левая боковая сто­рона прямоугольника;

(б) и в то же время она является не любой вер­тикалью, а частью треугольника;

(в) и, как таковая, она переносится, сдвигается вправо и становится соответствующей правой стороной прямоугольника.

Пункты (а) и (б) уже подразумевают двойную функ-

цию ¹ этой линии — она замыкает треугольник и образует левый край прямоугольника. Линия (в) сдвигается впра­во вместе со всем треугольником, выполняя здесь функ­цию правого края прямоугольника.

Второй перпендикуляр тоже является не просто ка­кой-нибудь линией, проведенной из вершины, а возника­ет как правильный край прямоугольника, будучи недо­стающей стороной треугольника.

И продолжение основания возникает не просто как какое-то произвольное продолжение линии, а как часть необходимого треугольника, дополняющая основание пря­моугольника.

Эти три линии возникают не как линии, а как грани­цы; главную роль играют не линии, а фигуры — парал­лелограмм, прямоугольник, треугольник; линии же высту­пают как части этих фигур.

2) Что же происходит с линиями исходной фигуры? Некоторые испытуемые описывают эти изменения. Снача­ла фигура рассматривается как параллелограмм, горизон­тальные стороны которого соединены косыми линиями.

Рис. 32

¹ Wertheimer M. Untersuchungen zur Lehre von der Ge­stalt. — "Psychologische Forschung", 1923, Vol. IV, S. 301—350; см. также: E11 i s W. D. Op. cit, selection 5, или Beardslee D. C. and Wertheimer M. (eds.). Readings in perception. Princeton, Van Nostrand, 1958, p. 115—135; Kopf ermann Н. Psychologische "Untersuchungen über die Wirkung zweidimensionaler Darstellungen körperlicher Gebilde. — "Psychologische Forschung". 1930. Vol. XII S. 295—364.

ше (не соответствует левому краю верхней горизонтали, он рассматривается отдельно как основание треугольника. Правая часть основания кажется незавершенной, лишен­ной необходимого конца.

Две наклонные стороны начинают вызывать беспокой­ство: «Края фигуры не должны выглядеть таким обра­зом»; возникает вектор, побуждающий нас не рассматри­вать стороны как пограничные линии; в результате пере­мещения треугольника они внезапно отождествляются, воспринимаются не как две линии, а как одна, и эта ли­ния уже не является пограничной, фактически теперь она не имеет структурного значения.

То же самое происходит и в случае первого решения (с. 77), и в решении с кольцом: проводимая вертикальная линия выполняет двойную функцию, будучи правильными левым и правым краями прямоугольника. (Действительное понимание роли линии предполагает такое расщепление на два функциональных элемента.) Наклонные же линии отождествляются и в новой структуре исчезают.

Аналогичные изменения наблюдаются и в восприятии. В этой области сравнимыми оказываются как структура событий, так и величины действующих сил.

Вот простой пример ¹: показанные ниже две черные

Рис. 33

фигуры вырезаются из дерева или картона и помещаются на белом фоне. Понаблюдайте за тем, как кто-нибудь бу­дет медленно двигать их друг к другу. Сойдутся ли они? Сомкнутся ли? Когда они приблизятся друг к другу — и сомкнутся. — зигзагообразные края вдруг исчезнут в едином однородном, лишенном всяких нарушений прямо­угольнике ². А что произойдет с наблюдателем, если в конце спокойного, медленного горизонтального движения

¹ См.: Wertheimer M. Zu dem Problem der Unterscheidung von Einzelinhalt und Teil. — "Zeitschrift für Psychologie", 1933, vol. 129, S. 353—357 (см. Приложение 1).

² Сравните также квадратные наборы из гл. 4, с. 159.

направление его внезапно несколько изменится? Некото­рые дети вскакивают, чтобы восстановить направление движения и правильно соединить части.

То же самое происходит и в наших задачах с парал­лелограммом: размышляя над задачей, ребенок приходит к мысли отрезать треугольник с левого края; вы берете треугольник, чтобы перенести его направо; как будут реагировать дети, если вы оставите треугольник в следую­щих положениях?

Рис. 34

Некоторые дети застывают от изумления, другие сме­ются, а третьи активно вмешиваются, чтобы правильно расположить треугольник.

Интересно наблюдать за поведением детей (даже очень маленьких) в следующих ситуациях. Детям предлагают четыре твердые фигуры, показанные на рис. 35 ¹.

¹ См.: Wertheimer M. Zum Problem der Schwelle.—"Be­richt über den VIII Internationalen Kongress für Psychologie", Gro­ningen, 1926.

Рис. 35

У детей часто наблюдается сильная тенденция правильно соединять фигуры: присоединить с к a, d к b. Когда взрос­лые пытаются сделать иначе, упорно соединяя фигуру d с а и с с b, или соединяют фигуру с с а и d с b, но непра­вильно, дети часто не просто удивляются или забавляются, но активно вмешиваются и правильно размещают фигу­ры ¹.

Во всех случаях мы сталкиваемся со структурными изменениями, стремлением к лучшей структуре, к согла­сованию частей и устранению нарушений.

В продуктивных процессах такие изменения являются часто весьма драматичными, куда более драматичными, чем в нашем скромном примере с параллелограммом. Дей­ствительно, весь процесс нередко представляет собой на­стоящую драму, движимую мощными силами, с присущи­ми ей напряжением и драматическими структурными из­менениями при переходе от неполной или неадекватной структуры к структуре завершенной и гармоничной ², при

¹ Очень легко пройти мимо реальных проблем, ссылаясь на то, что испытуемым «знакомы» такие завершенные фигуры (см. пункт 38). Часто фактор «знакомости» действует в том же направ­лении, что и фактор «хорошего гештальта», однако задача реша­ется и в тех случаях, когда фигура с хорошей структурой является менее знакомой, а фигура с менее совершенной структурой — бо­лее знакомой. Этот способ решения может быть применен ко всем структурам. Krolik W. Über Erfahrungswirkungen beim Bewe­gungssehen. — "Psychologische Forschung", 1934, Vol. 20, S. 47—101; Нubbel M. B. Configurational properties considered 'good' by nai­ve subjects. — "American Journal of Psychology", 1940, vol. 53, p. 46—69.

² См. Wertheimer M. Zu dem Problem der Unterscheidung von Einzelinhalt und Teil. — "Zeitschrift für Psychologie", 1933, Vol. 129, S. 353—357.

С помощью экспериментального набора, описанного на с. 356 этой статьи, можно четко выявить характерные особенности мно­гих процессов мышления. Сначала предъявляется простая фигура из точек; затем появляются вполне осмысленные добавления, со-

переходе от структурной слепоты и беспокойства к дей­ствительному пониманию задачи и ее требований.

36. В экспериментальном исследовании этих проблем гораздо важнее получить не количественный ответ на во­прос: «Сколько детей решили или не решили задачу и в каком возрасте?» и т. д., а понять, что происходит в хо­роших и плохих процессах мышления.

Физик, изучающий процесс кристаллизации, старается определить, как часто встречаются чистые кристаллы и как часто — деформированные кристаллы с зазубренными краями, кристаллы с примесями, сросшиеся, как сиамские близнецы, двойные кристаллы и даже искусственные от­полированные кристаллы, форма которых совершенно не соответствует их природе. Все эти случаи представляют первостепенный интерес для физика, но не с точки зре­ния статистики, а с точки зрения того, что они могут сообщить о внутренней природе самой кристаллизации.

Столь же важно выяснить, при каких условиях может происходить чистая кристаллизация, какие условия ей благоприятствуют и какие факторы грозят ее нарушить.

Так же обстоит дело и в психологии.

IV

37. Можно объяснить проще? Роль прошлого опыта?

Мой мудрый друг, которому я рассказал о решении с ножницами, воскликнул: «Этот ребенок — гений». Но мно­гие психологи скажут: «Ну и что? Очевидно, дело тут в прошлом опыте. К чему такие сложные и трудные объ­яснения? Не проще ли в полном соответствии со многими другими психическими процессами рассматривать то, что делают эти дети, просто как припоминание прошлого опы­та? Случайно или посредством каких-то механизмов ас-

держащие некую структурную незавершенность, которую следует устранить; но теперь рядом появляется новый набор, который по­ражает наблюдателя своей бессмысленностью, нелепостью и оза­дачивает его. Зато какое неожиданное облегчение наступает, когда после введения еще некоторых деталей все части внезапно образу­ют единое согласованное целое, по-новому ориентированное, сильно реорганизованное и перецентрированное в соответствии со струк­турными требованиями. Часто можно наблюдать у испытуемых признаки сильного напряжения, удивления, неуверенности и в ито­ге — неожиданного облегчения. Впоследствии испытуемые очень ярко описывают поразительную структурную динамику ситуаций. (см. Приложение 1).

социации ребенок вспоминает связанный с ножницами прошлый опыт. Остальные дети не смогли решить задачу потому, что они не вспомнили прошлый опыт, или пото­му, что у них не было достаточного опыта работы с нож­ницами. Они не усвоили связь, ассоциацию, которая могла бы им помочь, или же не вспомнили ее. Таким образом, все зависит от припоминания усвоенных связей. Именно память и вспоминание лежат в основе этого процесса.

Конечно, иногда к использованию ножниц приходят случайно или в результате припоминания внешних об­стоятельств. Случается, что даже в хороших процессах подсказки памяти либо проверяются и используются, ли­бо отвергаются как бесполезные. Нет никакого сомнения в том, что для того, чтобы эти процессы стали возможны­ми или вероятными, помимо настоящего опыта (что бы это ни значило), необходим значительный прошлый опыт.

Но адекватно ли для обсуждения таких вопросов ис­пользование лишь теоретических обобщений? Например, в пашем случае утверждают, что решающим обстоятель­ством является то, что ребенок вспоминает о ножницах и связанных с ними действиях.

Допустим, что ребенок, старающийся решить задачу, не думает о ножницах. Это содержание и связанные с ним ассоциации отсутствуют. Почему бы не взять теоре­тического быка за рога? ¹ Давайте дадим детям все необ­ходимое и посмотрим, что из этого выйдет. Если самым важным является припоминание опыта, связанного с упот­реблением ножниц, то мы можем сразу же снабдить ре­бенка ножницами и не обременять его память необходи­мостью вспомнить о них. Или можно ввести стимулы, об­легчающие такое припоминание.

В начале эксперимента я кладу ножницы на стол или даже прошу ребенка разрезать какой-нибудь лист бума­ги. Иногда это помогает (например, когда я показываю ножницы после некоторого периода колебаний у ребенка, после некоторых замечаний, свидетельствующих о том, что ребенок почувствовал структурные требования).

Но в некоторых случаях это не помогает. Ребенок смотрит на ножницы, потом — опять на чертеж. Видя их рядом, он явно начинает испытывать какое-то беспокой­ство, но ничего не предпринимает.

¹ См.: Maier N. R. F. Reasoning in humans: The solution of a problem and its appearance in consciousness.—"Journal of Compara­tive Psychology", 1931, vol. 12, p. 181—194.

Я усиливаю «помощь». «Не хочешь ли ты взять нож­ницы и разрезать фигуру?» В ответ ребенок иногда бес­смысленно смотрит на меня: он, очевидно, не понимает, что я имею в виду. Иногда дети начинают покорно раз­резать фигуру тем или иным способом:

Рис. 36

Бывает, что ребенок вслед за этим начинает составлять из двух частей другой параллелограмм...

Рис. 37

В каких же случаях помогает предъявление ножниц, а в каких — не помогает? Мы видим, что предъявление ножниц и их обычное употребление сами по себе не ока­зывают никакой помощи; они могут привести к совершен­но нелепым и слепым действиям. Короче говоря, они, видимо, помогают в том случае, если ребенок уже начи­нает осознавать структурные требования задачи или если они проясняются с помощью ножниц ¹; последние почти не помогают в тех случаях, когда испытуемый не осозна­ет структурные требования, когда он не рассматривает ножницы в связи с их функцией, их ролью в данном контексте, в связи со структурными требованиями самой ситуации. В таких случаях ножницы являются лишь еще одним предметом наряду с другими. Действительно, в не­которых позитивных процессах имели место попытки, сви-

Дата добавления: 2015-07-25