Основные законы автоматического регулирования: П-закон, И-закон, ПИ-закон и ПИД-закон.

Самым простым непрерывным законом регулирования является пропорциональный закон или П- закон. На рис. 1 а схематично показана поплавковая камера карбюратора двигателя внутреннего сгорания, где используется П- закон регулирования уровня топлива. На рис. 1 б представлена функциональная схема данной системы автоматического регулирования. Управляемой величиной y здесь является уровень топлива в камере, а управляющим воздействием U -–площадь открытия игольчатого клапана. Задающее воздействие (уставка) y₀ определяется высотой закрепления поплавка. При уменьшении уровня топлива в камере поплавок опускается и перемещает иглу клапана. Чем больше опускается поплавок, тем больше площадь открытия клапана и тем больше поступает топлива в камеру. Таким образом, управляющее воздействие U и разность между заданным значением управляемой величины y₀ и ее реальным значением y связаны жестким образом: U прямо пропорциональна , то есть U=ke, где k - коэффициент пропорциональности. На рис. 2 показана кривая регулирования при пропорциональном законе. При внезапном уменьшении уровня (начале расхода) топлива клапан открывается и в камеру начинает поступать топливо. Уровень его начинает монотонно увеличиваться. Однако, если расход топлива продолжается, то через некоторый промежуток времени наступает равновесное состояние: сколько топлива вливается, столько и выливается. Уровень его остается постоянным, но не равным заданному y₀. Между ними существует разница, которая называется статической ошибкойd. Чем больше расход топлива, тем больше статическая ошибка. Поэтому системы автоматического регулирования, использующие пропорциональный закон регулирования называют еще статическимисистемами. Статическая ошибка обусловлена жесткой связью между управляющим воздействием и отклонением управляемой величины от заданного значения. Чтобы избавиться от нее применяются законы регулирования с гибкой связью.

Интегральный закон регулирования (И- закон) математически формулируется следующим образом: 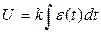, то есть управляющее воздействие является интегральной величиной от отклонения управляемой величины. На рис. 1.10 показана кривая процесса регулирования при использовании интегрального закона регулирования. В этом случае статическая ошибка отсутствует, но наблюдаются значительные колебания управляемой величины относительно заданного значения, которые обусловлены инерционностью объекта управления. Первый выброс в противоположную сторону от установившегося значения принято называть перерегулированием s. Системы автоматического регулирования без статической ошибки принято называть астатическими системами.

Для уменьшения перерегулирования и колебаний управляемой величины используется пропорционально- интегральный закон (ПИ-закон) регулирования, который представляет собой комбинацию пропорционального и интегрального законов: . На рис. 1.10 показана кривая регулирования для этого закона.

1. Дискретные законы автоматического регулирования: релейный и импульсный.

Под законом регулирования в автоматике понимают математическую зависимость, по которой автоматическое управляющее устройство (АУУ) – регулятор воздействует на объект управления, т.е. зависимость между управляющим воздействием U(t) и разницей между заданным значение y₀(t) и реальным значением y(t) управляемой величины : .

По способу передачи управляющего воздействия на объект управления законы регулирования делятся на непрерывные и дискретные. В системах регулирования с непрерывным законом регулирования управляющее воздействие U(t) непрерывно во времени. Если же, в процессе работы системы, при непрерывном сигнале ошибки e управляющее воздействие U(t) прерывается в некоторые промежутки времени или подается в форме отдельных импульсов, то такой закон регулирования называется дискретным. Наиболее простыми и самыми распространенными являются системы автоматического регулирования, использующие разновидность дискретного закона регулирования – релейный двухпозиционный закон регулирования. При этом законе управляющее воздействие, в зависимости от значения ошибки e, может принимать только два фиксированных значения: включено – выключено, вверх – вниз, вперед – назад и т.д. На рис. 1.6 а показана данная зависимость. Релейный закон регулирования технически легко реализовать, он наиболее часто встречается в повседневной жизни. На его основе построена работа таких устройств бытовой техники, как, например, холодильник, электроутюг, обогреватель и т.д. Для его реализации необходим датчик с релейным выходом, т.е. датчик должен скачкообразно изменять выходную величину в зависимости от изменения управляемой величины. На рис. 1.6 б показана схема автоматического регулирования температуры воды электрического водонагревателя с релейным законом регулирования. Для измерения температуры воды используется биметаллический датчик, состоящий из биметаллической пластинки и электрических контактов SK. Вода нагревается ТЭНом, который включается с помощью магнитного пускателя KM. При достижении заданной температуры, биметаллическая пластинка датчика нагревается и соответственно изгибается, размыкая электрический контакт SK, который включен в цепь катушки магнитного пускателя KM. Магнитный пускатель отключает ТЭН и вода начинает охлаждаться. При охлаждении до определенной температуры биметаллическая пластинка выпрямляется и замыкает контакт в цепи катушки магнитного пускателя. Процесс нагрева повторяется и т.д. На рис.1.6 в показана кривая изменения температуры воды при подобном законе регулирования. Из нее видно, что управляемая величина (температура) не постоянна во времени, а все время колеблется относительно некоторой средней величины. Амплитуда этих колебаний зависит от свойств объекта управления (его инерционности) и может достигать значительной величины. Таким образом, релейный закон регулирования не обеспечивает достаточной точности регулирования.

1. Математическое описание систем автоматического регулирования в динамическом режиме. Понятие передаточной функции. Комплексная передаточная функция и частотные характеристики.

При исследовании и расчетах систем автоматического регулирования используется операционная форма записи. Она основана на использовании преобразования Лапласа. Преобразование Лапласа позволяет функцию x(t) одного переменного (времени t) преобразовать в функцию другого переменного x(s) (s=a+jb – комплексное число) посредством соотношения . Функция x(t) называется оригиналом, а x(s) – изображением. Сокращенно преобразование Лапласа записывается как . Обратная операция, т.е. нахождение функции x(t) по ее изображению x(s) называется обратным преобразованием Лапласа: . При использовании преобразования Лапласа первая производная от x будет иметь изображение , вторая 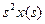, третья и т.д. Интеграл от будет иметь изображение . Если применить преобразование Лапласа к дифференциальному уравнению, то при нулевых начальных условиях оно примет вид . Это уравнение — алгебраическое, в нем s является независимой комплексной переменной, а величины х(s) и y(s) являются только изображениями физических величин х (t) и y (t). Символ s является алгебраическим числом.

Операционная форма записи уравнений элементов проста и удобна, так как преобразовать и решить алгебраическое уравнение несравненно проще, чем дифференциальное. Именно это и обеспечило ее широкое применение в теории автоматического управления.

Для оценки динамики систем может служить также операционное уравнение, из которого получается передаточная функция - отношение изображения выходной величины к изображению входной величины системы. Если, например, операционное уравнение имеет вид , то передаточная функция системы .

Если на вход линейной и устойчивой разомкнутой системы подать гармоническое возмущение, то по истечении времени протекания переходного процесса на выходе ее также установится гармоническое изменение выходной величины. По полученным значения x и y для различных значений частоты w получают частотные характеристики: амплитудную, частотную и амплитудно -фазовую. Амплитудно-частотная характеристика (АЧХ) есть зависимость отношения амплитуды колебаний на выходе Y_m к амплитуде колебаний на входе X_m от частоты колебаний w: . Фазо-частотная характеристика (ФЧХ) отражает зависимость фазового угла сдвига между входными и выходными колебаниями . Частотные характеристики можно определить, если известна передаточная функция звена W(s). . Поэтому, если положить , то можно записать выражение . Таким образом, если в выражение для передаточной функции подставить чисто мнимое значение ее переменной , то получим ее форму, называемую частотной передаточнойфункцией или амплитудно-фазовой характеристикой 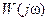. Функция 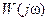при каждом значении частоты w является комплексной величиной и поэтому может быть представлена в показательной форме: , где , и называют соответственно модулем и аргументом частотной передаточной функции. 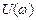В алгебраической форме функция может быть представлена как: , где, соответственно, — вещественная, а — мнимая части функции. Амплитудно-частотная характеристика является модулем этой комплексной функции: 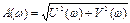, а фазо- частотная характеристика определяется как .

1. Показатели качества процесса регулирования.

Форма кривой переходного процесса характеризуется так называемыми показателями качества системы регулирования. Принято различать следующие показатели качества устойчивой системы (рис. 2.1). 1. Время регулирования или время переходного процесса, т. е. время, в течение которого заканчивается переходный процесс. По истечении этого времени , где - установившееся значение y при , — малая заданная величина, определяе мая обычно нечувствительностью регулятора 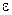. Время регулирования характеризует быстродействие системы. Чем меньше это время, тем выше быстродействие. Быстродействие является важнейшим показателем качества, нередко определяющим при проектировании структуру схемы и применение тех или иных элементов системы. 2. Перерегулирование, характеризующее максимальное отклонение регулируемой величины от установившегося значения. Перерегулирование определяется как .3. Колебательность процесса регулирования, который характеризуют числом колебаний регулируемой величины в переходном процессе. 4. Нечувствительность системы регулирования 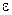. Под этим показателем качества понимают максимальные отклонения регулируемой величины от установившегося значения, в пределах которых регулятор не оказывает регулирующего воздействия. Нечувствительность системы зависит от сил сухого трения в отдельных элементах, от зазоров, мертвых ходов и т. д. В современных системах нечувствительность доведена до очень малых значений. 5. Статическая ошибка , определяющая статическую точность регулирования. Хотя статическая ошибка характеризует статический, установившийся режим, ее обычно рассматривают как один из показателей качества динамической системы в целом. Говорят, что система обладает требуемым качеством, если время регулирования, перерегулирование, колебательность, нечувствительность и статическая ошибка не превышают некоторых заранее заданных значений. В зависимости от назначения регулятора требования к качеству могут быть различными. В некоторых случаях, например, требуется, чтобы переходный процесс протекал вообще без колебаний и перерегулирования.

1. Определение устойчивости систем автоматического управления.

Поведение системы в переходном процессе можно представить в виде суммы двух составляющих: . Первая из них, - свободное движение системы, то есть движение системы, выведенной из состояния равновесия начальными условиями и представленной самой себе. Вторая, 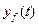- вынужденное движение системы, обусловленное внешним воздействием. Применительно к выражению, условие устойчивости системы можно сформулировать следующим образом. Система устойчива, если с течением времени от начала переходного процесса его свободная составляющая стремиться к нулю: . Передаточная функция системы автоматического управления относительно любого возмущения имеет следующий вид , где , - соответствующие полиномы от s. Если обозначить входное воздействие на систему (изменение задания или внешнее возмущение) как x(s), а ее реакцию (переходной процесс) как y(s), то, используя определение передаточной функции , выражение можно переписать как . Применим к уравнению обратное преобразование Лапласа. Получим линейное дифференциальное уравнение с правой частью. Решением данного уравнения и будет кривая переходного процесса y(t). Свободное движение системы определяется как решение однородного дифференциального уравнения с нулевой правой частью . Решение однородного дифференциального уравнения свободного движения имеет вид , где - постоянные интегрирования; - корни характеристического уравнения. Характеристическое уравнение . Каждому вещественному корню в выражении соответствует составляющая решения, имеющая вид показательной функции , характер которой зависит от знака корня. Если корень положителен (), то с ростом t значение y будет возрастать (кривая 1 на рис. 5.2а). Если же корень отрицателен (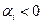), то соответствующая ему составляющая будет убывать и с течением времени стремиться к нулю (кривая 2 на рис. 5.2а). Если все корни характеристического уравнения вещественны и отрицательны, то и все выражение (5.7) с течением времени будет стремиться к нулю. Наличие хотя бы одного положительного корня приведет к тому, что с течением времени составляющая будет стремиться к бесконечности, то есть нарушается условие устойчивости системы (5.2). Если хотя бы один из корней окажется равным нулю (при всех прочих отрицательных корнях), то одна из составляющих при любых значениях времени будет постоянной, вследствие чего условие устойчивости (5.2) также не будет соблюдаться. Следовательно, необходимым условием устойчивости системы является условие отрицательности всех вещественных корней характеристического уравнения, полученного из характеристического многочлена передаточной функции системы. Если корни характеристического уравнения комплексные, то каждая пара комплексных сопряженных корней и дает составляющую переходного процесса в виде произведения показательной и синусоидальной функций. При отрицательном значении вещественной части корня, амплитуда данной составляющей стремиться к нулю (кривая 2 на рис. 5.2б), а при положительном – возрастает с течением времени (кривая 1 на рис. 5.2б). При чисто мнимом корне (вещественная часть равна нулю) получаем составляющую с незатухающими синусоидальными колебаниями.

Чтобы все составляющие решения дифференциального уравнения (5.7), относящиеся к комплексным корням с течением времени затухали, необходимо, чтобы вещественные части всех комплексных корней были отрицательными. Таким образом, необходимым и достаточным условием устойчивости линейной системы автоматического управления является отрицательное значение вещественной части всех корней характеристического уравнения, построенного по характеристическому многочлену передаточной функции системы.

1. Основные характеристики объекта управления и выбор закона регулирования.

. В зависимости от вида переходной характеристики (кривой разгона) задаются чаще всего простейшим видом передаточной функции объекта управления: в виде передаточной функции инерционного звена первого порядка и звена запаздывания ,где k - коэффициент передачи объекта; T - постоянная времени объекта; - время чистого запаздывание, которые должны быть определены в окрестности номинального режима работы объекта.

В каждом конкретном случае автоматизации возникает задача выбора закона регулирования, который смог бы обеспечить при реальных возмущениях требуемое качество процесса регулирования. Если необходимое качество может быть достигнуто не одним, а несколькими законами регулирования, то при выборе конкретного регулятора, выпускаемого промышленностью или вновь конструируемого, предпочтение отдается наиболее надежному и недорогому. Обычно самыми недорогими являются двух и трех позиционные релейные регуляторы. Сложность и стоимость регуляторов нарастают при осуществлении ими соответственно следующих законов регулирования: П, ПИ, ПИД.

Основой выбора закона регулирования является соотношение между временем запаздывания объекта t и постоянной времени T (20 – 21). Для большинства объектов регулирования рекомендуется при применять релейные законы регулирования, при - линейные законы (П, И, ПИ и ПИД), а при - импульсные законы.

1. Классификация датчиков температуры по принципу действия и области применения.

Методы и приборы для измерения температуры разделяют на две группы: бесконтактные и контактные.

Бесконтактные методы используют тепловое излучение, имеющее место в любых телах при любых температурах. Приборы, основанные на таком принципе, называются пирометрами.

Более широко распространены контактные методы измерения. Здесь, по принципу действия приборы для измерения температуры подразделяются на следующие группы.

- жидкостные, использующие свойство теплового расширения

- жидкостей;

- биметаллические и дилатометрические, использующие свойство теплового расширения твердых тел;

- манометрические, использующие зависимость между температурой и давлением газа, жидкости или пара в замкнутом объеме;

- термометры сопротивления, использующие зависимость электрического сопротивления вещества от его температуры;

- термоэлектрические, действие которых основано на измерении термо-эдс, создаваемой термопарой из двух разнородных проводников.

1. Классификация датчиков давления и расхода газов и жидкостей по принципу действия и области применения.

Расход - это количество вещества, протекающее через данное сечение канала в единицу времени. Количество вещества может быть выражено в единицах массы (кг,г)или в единицах объема (м). Соответственно различают: массовый расход S г/с и объемный расход, Q м/с. Приборы для измерения расхода называются расходомерами, а для определения количества вещества - счетчиками. Иногда применяется расходомер со счетчиком для одновременного измерения расхода и количества вещества. Эти приборы в основном, применяются на животноводческих комплексах для измерения расхода жидкостей (теплоноситель в системе отопления, техническая и питьевая вода, жидкий корм, навозные стоки, молоко и т.д.), расхода газов (воздух в системе вентиляции, газ в системе отопления) и расхода сыпучих сред (комбикормов, гранул и т.д.). Кроме того, с помощью расходомеров производится автоматическое дозирование и поддержание заданного соотношения между расходами двух или нескольких компонентов. Приборы для измерения расхода и количества можно разделить на следующие группы: переменного перепада давления, постоянного перепада давления, индукционные, ультразвуковые, счетчики скоростные, объемные и массовые.

Приборы этого типа преобразуют разность давлений среды, протекающей через установленное в трубопроводе сужающее устройство, в показания расхода. Поток жидкости, протекающий в трубопроводе, непрерывен и количество ее в любом сечении постоянно. Поэтому, если в трубопроводе установить диафрагмы (рис. 6), проходной диаметр которой меньше диаметра трубопровода, то скорость потока в этом месте возрастет. Перепад (разность) давления перед диафрагмой и после нее зависит от расхода протекающего вещества и может служить мерой расхода. Перепад давления измеряется любым дифференциальным манометром. Таким образом, установка для измерения расхода по методу переменного перепада давления состоит из сужающего устройства, дифманометра, соединительных трубок и уравнительных сосудов..

Расходомеры постоянного перепада или расходомеры обтекания применяют для измерения малых расходов жидкостей и газа. Действие их основано на измерении положения поплавка или поршня в потоке при постоянном перепаде давления В стеклянную конусную трубку I, закрепленную вертикально в головках корпуса, помещен поплавок 2. Поток измеряемой жидкости движется снизу вверх и поднимает поплавок, который за счет косых прорезей в верхней части поворачивается, обеспечивая центрирование в трубе. Подъемная сила создается перепадом давления жидкости между нижней и верхней кромками поплавка и зависит от скорости потока и величины кольцевого зазора между ним и стенками. При подъеме поплавка в конусной трубке кольцевой зазор увеличивается, перепад давления уменьшается, и поплавок останавливается на уровне, соответствующем определенному расходу жидкости или газа. В индукционных расходомерах используется электромагнитный метод, который позволяет проводить измерения расхода в тех случаях, когда другие методы не пригодны. Так жидкие корма представляют собой вязкую, многокомпонентную абразивную жидкость, расход которой, как и навозных стоков, нельзя измерить с помощью диафрагмы или ротаметров. Принцип действия индукционных расходомеров основан на законе электромагнитной индукции, согласно которому наведенная в проводнике электродвижущая сила пропорциональна скорости V перемещения его в магнитном поле: E=BLV. Магнитное поле с индукцией B при этом создается электромагнитом 1 (рис. 8), а роль проводника 6, движущегося в магнитном поле, выполняет часть измеряемой электропроводной жидкости в отрезке немагнитной трубы 2. Наведенная в жидкости эдс Е пропорциональна скорости потока V и может являться мерой расхода жидкости, Она снимается двумя электродами и подается на усилитель 3.

1. Классификация датчиков уровня жидкостей и сыпучих тел по принципу действия и области применения.

Действие поплавковых уровнемеров (рис. 2) основано на принципе использования выталкивающей силы жидкости. Основные элементы таких устройств: поплавок 1, передаточный механизм 2 и отсчетное устройство 3. Плавающий на поверхности жидкости поплавок является чувствительным элементом для измерения уровня. Подъемная сила поплавка зависит от его объема и плотности жидкости. Передаточные механизмы могут быть гибкими (трос, лента, нить), жесткими (рычаг, рейка) или магнитными. Буйковые уровнемеры работают в соответствии с законом Архимеда (рис. 3). Чувствительный элемент уровнемера - буй представляет собой полый цилиндр, помещенный в сосуд с измеряемой жидкостью. Выталкивающая сила, действующая на буй и пропорциональная уровню жидкости, воспринимается системой подвески буя и преобразуется в электрический сигнал. Длина буя выбирается равной или несколько больше диапазона измерения уровня. Гидростатические уровнемеры определяют давление столба жидкости в сосуде. По разности давлений на дне сосуда и на поверхности жидкости определяется ее уровень (рис. 4). В качестве чувствительного элемента гидростатического уровнемера может быть использован любой датчик давления или дифманометр. При соприкосновении проводящей жидкости с проводником (электродом) происходит скачкообразное изменение сопротивления электрической цепи между ним и уровнем жидкости от бесконечности до конечной величины. Этот "релейный эффект" лежит в основе принципа действия широко применяемых контактных или кондуктометрических сигнализаторов уровня. Их первичные преобразователи представляют собой электрически изолированные от корпуса сосуда стержни (электроды), установленные в сосуде на определенном уровне. На рис. 5 показан один из вариантов такого сигнализатора, применяемого для автоматизации башенных водокачек. Электроды нижнего (НУ) и верхнего (ВУ) уровней устанавливаются на необходимое расстояние в башне. Вместе с общим электродом (0) они образуют два электрических контакта, схема которых представлена на рис. 5 6. При достижении водой нижнего уровня замыкается контакт SL2, а при достижении верхнего - контакт SL1. Для обеспечения безопасности электроды сигнализатора включаются в низковольтную электрическую цепь (12...24 В).

Принцип действия емкостных уровнемеров основан на том, что диэлектрическая проницаемость водных растворов солей, кислот и щелочей отличается от диэлектрической проницаемости воздуха или водных паров. ПИП емкостного уровнемера представляет собой изолированные электро ды, погруженные в измеряемую среду (рис. 6). Если корпус сосуда металлический, то достаточно одного электрода.

Электроды (электрод и корпус сосуда) образуют цилиндрический конденсатор, емкость которого изменяется при колебаниях уровня жидкости. Величина емкости этого конденсатора измеряется электронным блоком, который передает сигнал далее. Электроды емкостного уровнемера могут быть стержневые, кабельные или пластинчатые.

1. Классификация промышленных регуляторов по принципу действия и области применения.

Автоматические регуляторы классифицируются по назначению, принципу действия, конструктивным особенностям, виду используемой энергии, характеру изменения регулирующего воздействия и т.п. По принципу действия они подразделяются на регуляторы прямого и непрямого действия. Регуляторы прямого действия не используют внешнюю энергию для процессов управления, а используют энергию самого объекта управления (регулируемой среды). Примером таких регуляторов являются регуляторы давления. В автоматических регуляторах непрямого действия для его работы требуется внешний источник энергии. По роду действия регуляторы делятся на непрерывные и дискретные. Дискретные регуляторы, в свою очередь, подразделяются на релейные, цифровые и импульсные. По виду используемой энергии они подразделяются на электрические (электронные), пневматические, гидравлические, механические и комбинированные. Выбор регулятора по виду используемой энергии определяется характером объекта регулирования и особенностями автоматической системы. По закону регулирования они делятся на двух- и трехпозиционные регуляторы, типовые регуляторы (интегральные, пропорциональны, пропорционально-дифференциальные, пропорционально-интегральные, и пропорционально-интегрально-дифференциальные регуляторы - сокращенно И, П, ПД, ПИ и ПИД - регуляторы), регуляторы с переменной структурой, адаптивные (самонастраивающиеся) и оптимальные регуляторы. Двухпозиционные регуляторы нашли широкое распространение, благодаря своей простоте и малой стоимости. По назначению регуляторы подразделяются на специализированные (например, регуляторы уровня, давления, температуры и т.д.) и универсальные с нормированными входными и выходными сигналами и пригодные для управления различными параметрами. По виду выполняемых функций регуляторы подразделяются на регуляторы автоматической стабилизации, программные, корректирующие, регуляторы соотношения параметров и другие.

1. Классификация реле времени и программных реле по принципу действия и области применения.

Реле времени представляют собой устройства, конструкция которых содержит специальный узел, обеспечивающий задержку появления (исчезновения) выходного сигнала после подачи (снятия) входного.

Выдержки времени до 5 с можно получить посредством несложных схемных решений, которые позволяют замедлить нарастание или спадание токов в обмотках электромагнитных реле постоянного тока.

Шунтирование обмотки реле резистором или диодом позволяет после отключения поддерживать некоторое время протекание тока по обмотке в прежнем направлении за счёт эдс самоиндукции, возникавшей в обмотке в момент коммутации, и тем самым замедлить время отпускания реле. Щунтирование обмотки реле конденсатором позволяет задержать время срабатывания реле. Подбором ёмкости конденсатора С и резистора R можно в широких пределах менять продолжительность времени задержки срабатывания реле.

Для создания выдержки времени в больших пределах применяются специальные реле времени, которые можно классифицировать по принципу действия на следующие группы: с электромагнитным замедлением, с пневматической задержкой, моторные реле времени, с часовым механизмом электронные и т. д.

В реле времени постоянного тока с электромагнитной задержкой задержка в срабатывании или отпускании создаётся электромагнитным демпфированием, осуществляемым специальной короткозамкнутой обмоткой или гильзой из меди, латуни или алюминия, размещённой на магнитопроводе реле. Эти реле просты и надёжны, выдержка времени составляет 0,15...10 с и зависит от толщины немагнитной прокладки между якорем и сердечником и натяжения пружины. Недостатки реле - большие габариты и небольшой диапазон выдержек времени.

В электромагнитных реле времени с пневматической задержкой задержка создаётся пневматическим механизмом, пристроенным к приводному механизму электромагнитного типа. Эти реле обеспечивают выдержку времени в диапазоне 0,2...180 с.

Для получения различных по величине регулируемых выдержек времени по нескольким выходным цепям широко применяются моторные реле времени. Реле ВС-10, установленное на стенде, представляет собой электромеханическое устройство с приводом от синхронного двигателя. Вращение от двигателя через редуктор передаётся диску сцепления, который свободно вращается на своей оси. При включении электромагнита диск оцепления притягивается к шестерне главной оси, входит с ней в зацепление, и начинает вращать главную ось, на которой расположен набор шкал (их может быть три или шесть),стянутых между собой при помощи зажимной гайки. Когда гайка отпущена, шкалы можно поворачивать одну относительно другой и тем самым задавать нужную программу выдержек времени.

Во время работы реле шкалы движутся и укреплённые на них упоры перебрасывают кулачки, а те переключают контактные системы.

После отработки программы размыкающий контакт концевого выключателя отключает двигатель реле, и главная ось со шкалами останавливается в том положении, которого они достигли.

Выключение электромагнита приводит к возврату шкал в исходное положение. При этом все контакты реле вновь окажутся в исходном положении и реле времени готово к новому включению. Эти реле выпускаются в различных модификациях с выдержками времени 2...60 с, 15с...9 мин, 1...24 час.

Двух программные реле времени 2РВМ применяются в тех случаях, когда необходимо выполнение суточного цикла программ. Такое реле состоит из анкерного часового механизма с автоматическим подзаводом пружины от электродвигателя и программного устройства. Основной частью программного устройства служит подвижная часовая шкала с двумя рядами отверстий, в которые согласно программам ввинчиваются установочные штифты. Во время движения шкалы штифты при помощи пружинно-рычажного механизма вызывают срабатывание микровыключателей программ. Микровыключатели подают питание на катушки выходных реле, которые и коммутируют цепи нагрузок.

В последнее время в различных системах сельскохозяйственной автоматики широкое распространение получают электронные реле времени. Они отличаются высокой надёжностью, малыми габаритами и имеют широкий диапазон исполнения по времени выдержки. В реле этой серии применяется либо принцип пересчёта импульсов, либо принцип интегрирования при помощи RC -цепи.

1. Основные положения алгебры логики. Бесконтактные логические элементы.

Логическими сообщениями называются такие сообщения, истинность или ложность которых может быть оценена однозначно. Например: "Двигатель включен"; "Уровень воды выше допустимого"; "По трубопроводу протекает молоко".

Каждое логическое сообщение может быть заменено математическим эквивалентом, логической функцией. Логическая функция (переменная) может принимать только два значения, называемые различными авторами ИСТИНА и ЛОЖЬ, TRUE и FALSE, ДА и НЕТ, 1 и 0. Наиболее распространено последнее обозначение. Логическая функция А=1, если логическое сообщение истинно (например "Двигатель включен", если он действительновключен) и А=0, если это сообщение ложное (двигатель на самом деле выключен). При этом 1 и 0 нельзя трактовать как числа, над ними нельзя производить арифметические действия. Это просто короткая, удобная форма обозначения понятий: ДА и НЕТ,

Логические переменные хорошо описывают состояние таких объектов, как реле, тумблеры, кнопки и т.д., то есть объектов, которые могут находиться в двух четко различных состояниях: включено - выключено. К этим объектам относятся и полупроводниковые элементы, на выходе которых может быть лишь один из двух четко различных уровней напряжения. Чаще более высокий, или просто ВЫСОКИЙ, уровень принимается за логическую единицу, а более низкий, или просто НИЗКИЙ, - за логический нуль.

Для математического описания связей между логическими сообщениями и функциями используются логические операции, основные из которых образуют алгебру логики.

Алгебра логики является аналогом обычной алгебры. Ее особен­ность заключается в том, что аргументы и функции принимают только два значения: 0 и 1. Алгебра логики выполняет следующие функции:

1. Позволяет математически записывать логические соображения и связи между ними, что необходимо для определения порядка и принципа работы устройства.

2. Позволяет реализовывать логические уравнения в виде логических схем, т.е. переходить от аналитического описания процесса к его схемной реализации в виде логического автомата.

3. Позволяет проводить реализацию логических автоматов в оптимальном виде (минимальное число элементов, их однородность, надежность функционирования и т.д.).

Порядок действий в алгебре логики следующий: сначала выполняется операция НЕ, затем И, и наконец ИЛИ. Как и в обычной алгебре, для изменения порядка действий используются скобки. Не следует забывать, что операций вычитания и деления в алгебре логики нет. Справедливы переместительный и сочетательный законы:

Операция НЕ (другие названия: логическое отрицание, инверсия) - это функция одного аргумента, функция обычно обозначается чертой над аргументом: 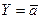, где y - логическая функция; - аргумент. Функция отрицания равна 1, когда ее аргумент равен 0, и наоборот, как это показано в таблице истинности. Пример: Логическая функция : «Первый двигатель включен». Функция : «Первый двигатель не включен». Отрицание отрицания аргумента равно самому аргументу: НЕ (НЕ ВКЛЮЧЕН) =ВКЛЮЧЕН, иди если

Операция И - это функция двух и большего числа аргументов (другие названия: логическое умножение, конъюнкция, совпадение). Обозначение: . Функция И равна 1 тогда и только тогда, когда все ее аргументы равны 1. Поэтому логическая операция И имеет тот же смысл, что и в обыденной речи: Например: «Двигатель включен, если закрыта крышка бункера и кнопка»

Операция ИЛИ - это функция двух и более аргументов (другое название: логическое сложение, дизъюнкция). Обозначается как: . Функция ИЛИ равна 1, если хотя бы один из ее аргументов равен 1. Логическая операция ИЛИ имеет тот же смысл, что и в обыденной речи. Например: «Двигатель можно включить кнопкой на пульте оператора или кнопкой у дробилки».

1. Основные принципы построения комбинационных логических схем.

Логические устройства, выходные функции которых однозначно определяются входными логическими функциями в тот же момент времени, называются комбинационными. Рассмотрим порядок построения комбинационного логического устройства на примере. Требуется создать логическое устройство для включения двигателя транспортера. Двигатель может быть включен кнопкой непосредственно на пульте управления (логическая функция a =1) или по команде с диспетчерского пульта (b= 1). Транспортер работает только тогда, когда включен последующий за ним транспортер (c =1).

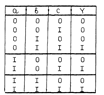Разобьем решение задачи на несколько этапов. 1-й этап - составление таблицы истинности. В соответствии с условиями задачи заполняем таблицу истинности, в которой записываем значение выходной функции Y в зависимости от входных функций a,b,c для всех возможных вариантов их сочетаний. При трех входных функциях сочетаний . 2 этап. Составление логического уравнения. Сведения, представленные в таблице истинности, необходимо записать в виде уравнения. Прежде всего, выделим строки таблицы, в которых Y=1. Это строки 4,6,8. Функция Y истинна, если входные переменные имеют значения, соответствующие любой их этих строк. Сформируем это словесно: «Функция Y истинна (равна 1), когда истинны не а и в, и с. (строка 4) или а и не в. и с (строка 6) или а и в и с (строка 8)». А теперь заменим слово не на знак операции НЕ, слово или на знак операции ИЛИ, а слово и на знак операции И. Получим . 3 этап. Минимизация функции. Можно создать логическое устройство, которое непосредственно реализует функцию. Тогда для выполнения двух инверсий будет необходимо два элемента НЕ, для триады выполняемой операции И необходимо три трехвходовых элемента И и, затем, операцию ИЛИ на одном трехвходовом элементе ИЛИ. Всего используем шесть элементов. Но выражение можно упростить. Вынесем за скобки общий множитель с: , а затем и множитель b: . 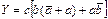Согласно тождества, выражение в круглых скобках . Произведение (тождество 8). В результате получим . Используя тождество (11) заменим выражение в круглых скобках . Тогда искомая функция примет конечный упрощенный вид: 4 этап. Составление логической схемы. Функция (15) содержит две операции ИЛИ и И. В соответствии с этим, схема, приведенная на рис. 5 выполнена на двух элементах. Порядок решения задачи, разбиваемой на 4 этапа, сохраняется, если разрабатываются и более сложные комбинационные устройства.

1. Программируемые логические контроллеры. Пример его применения для автоматизации водоснабжения.

Универсальные логические модули LOGO! предназначены для замены традиционных схем управления, выполненных на основе реле, контакторов и подобных им устройств.

Его достоинствами являются:

· широкий диапазон применения, например, для управления освещением, воротами и дверьми, контроль доступа, барьеры, системы обогрева и вентиляции;

· универсальность – одно LOGO! заменяет несколько десятков элементов релейной защиты и монтаж всех отдельных компонентов;

· надёжность

· уменьшение обычных рабочих временных затрат на внесение измерений, замену, расширение и модернизацию;

· сравнительно небольшая стоимость относительно суммарной стоимости всех заменяемых элементов.

Также логические модули имеют встроенные клавиатуру и дисплей. Для программирования модулей используются самые распространенные на практике логические функции, в том числе шесть базовых (AND, OR, NOT, NAND, NOR, XOR), а также ряд специализированных функций (задержка включения и выключения, импульсное реле, выключатель с часовым механизмом, реле с самоблокировкой, тактовый генератор и др.). Для хранения управляющей программы в модуле имеется встроенное энергонезависимое запоминающее устройство (EEPROM). Создание резервной копии программы, а также перенос ее на другие модули LOGO! могут быть осуществлены с помощью специальных модулей памяти.

---

Дата добавления: 2015-07-25