Универсальная абстрактная машина

Алгоритмы строятся из команд, а из алгоритмов можно строить более сложные алгоритмы [7].

1) Композиция C алгоритмов А, В:

C=А◦В

С=В(А(Х)), Х – исходные данные.

Таким образом, приписывается программа к программе (программа за программой).

2) Ветвление:

А, В, С, D.

Запускается алгоритм А.

Если результат применения А(Х) соответствует заданному условию, то D(Х)=B(Х).

Иначе, D(Х)=С(Х).

3) Итерация (повторение):

Повторение алгоритма А, пока алгоритм В не укажет, что пора заканчивать.

Более удобна, чем примитивные вышерассмотренные, так называемая универсальная машина U, которая выполняет, как и современная ЭВМ любую программу.

Такая машина читает произвольную запись программы Р и применяет ее к заданному слову. Таким образом, исходные данные – это запись программы Р и исходные данные Х.

(Р) – запись программы;

Х – исходные данные (на ленте);

(Р)*Х, где * – разделитель, символ не используемый в Р.

Тогда результат записывается как U((P)*X)=P(X).

Один из способов построения универсальной машины – использование геделевской нумерации алгоритмов [19].

Программу машины Тьюринга можно закодировать следующим образом. Представим в общем, виде команду:

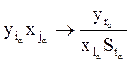, a=1...k,

где k – число программ (машин), S₁=L – налево, S₂=R – направо, S₃=E – на месте.

Пусть р₁, р₂, р_3, ... последовательность всех простых чисел, расположенных в порядке возрастания (т.е. последовательность 2,3,5,7,11,...). Номером машины Тьюринга М с программой n называется число:

Закодируем, например, машину Тьюринга М₁ с программой:

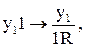
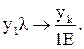
Здесь алфавит X₀={1,l}, Y₀={y₁,y_k}, кроме того t={1,2,3} соответствует L, R, E.

Таким образом:

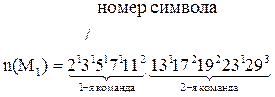
Естественно, не все натуральные числа являются номерами машин Тьюринга. Если n – номер некоторой машины, то ее программу можно однозначно установить по этому номеру.

Дата добавления: 2015-07-11