Алгоритм та інструкція до програми PPSMW розрахунку перехідних процесів у синхронних машинах

1 АЛГОРИТМ РОЗРАХУНКУ

Розрахунок електромагнітних та електромеханічних перехідних процесів у синхронних машинах можна виконати шляхом розв’язку системи диференціальних рівнянь, що отримали назву повних рівнянь Парка – Горєва. Повні рівняння перехідного процесу ― це рівняння математичної моделі машини, записані у прямокутній системі координат d, q, 0, що жорстко зв’язана з ротором. Для ненасиченої явнополюсної машини, що має на роторі окрім обмотки збудження заспокійливі замкнуті контури у поздовжній (d) і поперечній (q) осях, ці рівняння у взаємній системі відносних одиниць, але коли час та стала часу виражені у секундах, а кутова частота у рад/с, можуть бути записані у наступному виді, якщо не вводити спеціальних позначень для змінних у відносних одиницях (окрім рівняння для обмотки збудження):

;

;

;

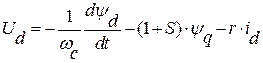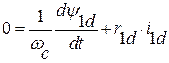; (1)

;

;

.

Якщо синхронна машина працює паралельно з системою необмеженої потужності, що характеризується вектором напруги 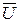, то складові напруги на виводах машини по осях d і q,

,

,

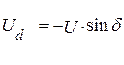тут 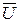, , - узагальнений вектор напруги на виводах машини та його складові по осях d і q, виражені в прийнятій системі відносних одиниць;

d - кут між поперечною віссю машини q і вектором напруги 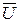, виражений у радіанах.

Система диференціальних рівнянь (1) доповнюється алгебраїчними рівняннями потокозчеплень, які встановлюють зв’язок між струмами контурів та їх потокозчепленнями. Враховуючи, що у відносних одиницях індуктивності і індуктивні опори рівні, вони мають вид:

,

,

, (2)

,

.

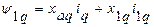У наведених рівняннях Парка – Горєва усі величини виражені у відносних одиницях при номінальних умовах синхронної машини:

x_d, x_q - синхронні індуктивні опори обмотки статора по поздовжній і поперечній осям;

x_ad, x_aq – індуктивні опори реакції статора (взаємоіндукції) по поздовжній і поперечній осям;

x_f, x_1d, x_1q – індуктивні опори обмотки збудження, поздовжньої і поперечної демпферних обмоток;

r, r_f, r_1d, r_1q - активні опори обмотки статора, обмотки збудження, поздовжньої і поперечної демпферних обмоток;

, , , , , - результуючі потокозчеплення (включаючи потокозчеплення розсіяння) і струми обмоток статора, збудження та демпферної обмотки по поздовжній осі;

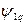, , , - результуючі потокозчеплення (включаючи потокозчеплення розсіяння) і струми обмотки статора, та демпферної обмотки по поперечній осі;

напруга, що підключена до кола збудження у відносних одиницях в долях напруги збудження холостого ходу;

- для генератора ― момент турбіни (вводиться у вихідних даних зі знаком мінус); для двигуна ― момент опору механізму (вводиться у вихідних даних зі знаком плюс).

- зведене значення сталої інерції агрегату генератор – турбіна чи двигун – механізм, с;

- ковзання ротора машини відносно синхронної осі, що обертається з постійною кутовою частотою , де - частота системи, = 50 Гц, ;

- кутова швидкість обертання ротору машини.

Перші п’ять рівнянь у (1) ― це рівняння електричної рівноваги статорних і роторних контурів, а шосте і сьоме― рівняння руху ротора. Усі параметри машини і змінні цих рівнянь виражені у взаємній системі відносних одиниць, а незалежна змінна (час) у секундах. У секундах виражена і стала інерції агрегату T_j.

Для синхронних двигунів з масивним ротором чи з масивними полюсами враховується витіснення струму у роторі уведенням залежностей зведених активного опору й опору розсіювання еквівалентного заспокійливого контуру від ковзання у вигляді

;

, якщо |s| > 0,05 та

, якщо |s| 0.05.

Тут: ― активний опір демпферної обмотки по поздовжній осі при малій частоті струму, тобто малих ковзаннях; , ― активний та індуктивний опори демпферної обмотки по поздовжній осі при пуску.

У взаємній системі відносних одиниць як базисні одиниці приймаються:

1. Для кутової частоти: w_б = w_с = 2p , при цьому базисна кутова швидкість ротора, 1/с:

,

де р - число пар полюсів машини.

2. Базисний струм - амплітуда номінального фазного струму статора, кА:

.

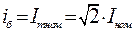3. Базисна напруга - амплітуда номінальної фазної напруги статора, кВ:

.

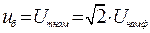Інші базисні величини для змінних статора визначаються наступними співвідношеннями:

4. Базисний опір статора, Ом:

.

5. Базисна потужність - номінальна потужність машини (статора), МВА

,

де U_{ном ф} і І_{ном ф} - діючі значення номінальних фазної напруги у кВ і струму статора у кА.

6. Базисна індуктивність статора, Генрі:

.

7. Базисне потокозчеплення статора, Вебер:

.

8. Базисний момент, нм

.

При вказаних базисних одиницях і синхронній кутовій частоті в мережі, тобто коли w = w_с = const і ,маємо

,

,

,

тобто індуктивний опір чисельно дорівнює індуктивності, а потокозчеплення чисельно рівне ЕРС або падінню напруги.

У взаємній системі відносних одиниць базисні величини для роторних контурів підкоряються приведеним вище співвідношенням, а базисна потужність приймається однаковою як для статора, так і для кожного з роторних контурів.

9. Базисний струм обмотки збудження

.

10. Базисна напруга обмотки збудження

.

11. Базисний опір обмотки збудження

,

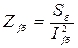тоді

.

Проте, відносний опір обмотки збудження зручніше визначати по постійній часу T_{f 0} обмотки збудження при усіх розімкнених контурах, з якими вона має магнітний зв'язок:

.

Для демпферних контурів потрібно також знаходити свій базисний струм, який відрізнятиметься від базисного струму збудження, оскільки для них буде інше число витків і інший обмотувальний коефіцієнт. Тому для демпферних контурів відносний опір також зручно визначати по постійних часу, які знаходяться експериментально або оцінюються по конструктивних розмірах машини.

У третьому рівнянні системи (1) - відносне значення струму збудження, приведеного до статора, у взаємній системі відносних одиниць, тобто 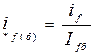. Але, коли розглядається лінеаризована характеристика холостого ходу синхронної машини у відносних одиницях, як залежність ЕРС холостого ходу від струму збудження, останній зручно виражати не відносно , а відносно струму збудження холостого ходу 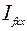, тобто як , оскільки коли у якості характеристики холостого ходу береться пряма, що проходить через початок координат і точку з координатами (1, 1), яка відповідає режиму холостого ходу, у якому при струмі збудження, що дорівнює струму збудження холостого ходу () ЕРС холостого ходу (інакше синхронна ЕРС E_q) дорівнює номінальній напрузі машини (), маємо співвідношення

.

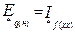Синхронну ЕРС у попередньому режимі, отже, і струм збудження легко визначити із векторної діаграми попереднього режиму. Струм збудження у відносних одиницях по відношенню до , що фігурує у рівняннях Парка – Горева, знаходиться як

.

Його значення у попередньому режимі легко визначається, оскільки легко, як вказано вище, знаходиться значення . По цій же причині у третьому рівнянні системи рівнянь Парка – Горєва (1) напруга, що підключена до кола збудження, для зручності виражена у відносних одиницях не відносно 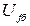, а відносно напруги збудження холостого ходу, оскільки, як показано в [ ] 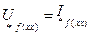і, отже,

,

тобто легко визначається із векторної діаграми попереднього режиму.

Для чисельного розв’язку система нелінійних рівнянь Парка – Горєва (1), (2) записується у формі Коші, тобто кожне з семи диференціальних рівнянь розв’язується відносно своєї похідної. У правій частині перетвореної системи фігурують параметри режиму― струми обмоток статора і ротора та їх потокозчеплення, які знаходяться шляхом розв’язку системи алгебраїчних рівнянь (2). Для підвищення стійкості розв’язку спочатку знаходяться потокозчеплення у повітряному зазорі, а потім струми усіх контурів.

Незалежна змінна ― час перехідного процесу розбивається на інтервали . Для розрахунку приросту залежних змінних , , 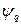, , , 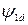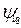s, δ на кожному кроці інтегрування у програмі PPSMW використовується метод Рунге - Кутта четвертого порядку. Кут d між віссю, що синхронно обертається, співпадаючою по напряму з вектором напруги 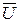чи з вектором ЕРС Е_с, і віссю q ротора при інтегруванні ковзання розраховується у радіанах.

Програма передбачає можливість розрахунку перехідного процесу у випадку, коли враховується індуктивний опір мережі системи x_c між виводами машини і точкою підключення джерела з незмінною напругою U_c = E_c = const. Опір системи враховується в рівняннях Парка – Горєва як збільшений індуктивний опір розсіяння обмотки статора, тому він повинен бути вираженим у відносних одиницях при номінальних умовах синхронної машини.

2 МЕТОДИКА РОЗРАХУНКУ ПАРАМЕТРІВ СИНХРОННОЇ МАШИНИ, ЗОВНІШНЬОЇ МЕРЕЖІ ТА ПОЧАТКОВИХ УМОВ, НЕОБХІДНИХ ДЛЯ МОДЕЛЮВАННЯ ПО РІВНЯННЯМ ПАРКА - ГОРЄВА

Дата добавления: 2015-07-12