
Читайте также:
|
Конструкция состоит из двух балок АС и ВС, соединенных между собой шарниром С. Связями для данной конструкции являются жесткая заделка в т. А и подвижный шарнир в т. В. Указанные связи, в соответствии с условием задачи, являются идеальными. Конструкция под действием внешних нагрузок находится в равновесии, а это означает, что данная механическая система (конструкция) имеет ноль степеней свободы.
1. Определение реакции RB.
Для определения реакции связи В мысленно отбрасываем эту связь, заменяя ее действие на конструкцию реакцией  этой связи. Таким образом, переводим реакцию
этой связи. Таким образом, переводим реакцию  в разряд внешних сил. Отбросив связь В и заменив ее реакцией
в разряд внешних сил. Отбросив связь В и заменив ее реакцией  , конструкция условно становится подвижной с одной степенью свободы потому, что балка АС осталась неподвижной, а балка ВС имеет возможность вращаться вокруг шарнира С (рис. Д7.3). Поэтому стало возможным дать возможное перемещение δφ
, конструкция условно становится подвижной с одной степенью свободы потому, что балка АС осталась неподвижной, а балка ВС имеет возможность вращаться вокруг шарнира С (рис. Д7.3). Поэтому стало возможным дать возможное перемещение δφ
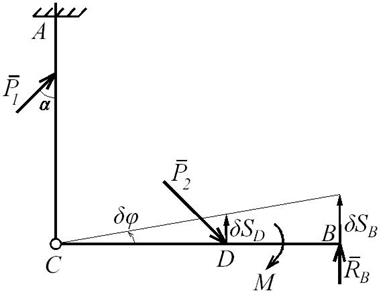
Рис. Д7.3
при вращении балки ВС вокруг шарнира С и составить одно уравнение равновесия на основе принципа возможных перемещений. Из этого уравнения и найдем искомую реакцию RB.
Переведя реакцию связи В в разряд внешних получаем, что на конструкцию действуют силы  ,
,  ,
,  и момент М. Связь А является идеальной, поэтому ее реакции не будут входить в уравнение принципа возможных перемещений.
и момент М. Связь А является идеальной, поэтому ее реакции не будут входить в уравнение принципа возможных перемещений.
Дадим конструкции возможное перемещение δφ и составим уравнение равновесия на основе принципа возможных перемещений:
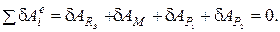 (1)
(1)
В уравнении (1) элементарные работы равны:
а) силы RB:

б) момента М:

здесь взят знак «минус» потому, что направление момента и элементарного угла поворота δφ противоположны;
в) силы P 1:
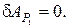
Элементарная работа силы  равна нулю потому, что приложена к неподвижной точке (возможное перемещение δφ относится только к балке ВС; балка АС при этом остается неподвижной);
равна нулю потому, что приложена к неподвижной точке (возможное перемещение δφ относится только к балке ВС; балка АС при этом остается неподвижной);
г) силы P 2:

где δ SD – возможное перемещение точки D (точки приложения силы  ).
).
Найдем соотношения между возможными перемещениями δφ, δ SВ и δ SD:

(2)
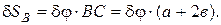
Подставим в уравнение (1) значения элементарных работ с учетом выражений (2):
 (3)
(3)
Так как δφ ≠ 0, то определим из уравнения (3) искомую реакцию RB:
 кН.
кН.
2. Определение реакций связи А.
Связь А – жесткое защемление. В общем случае реакции жесткого защемления складываются из реактивного момента МА и силы реакции, направление которой нам заранее неизвестно. Поэтому, при решении задач целесообразно силу реакции жесткого защемления разложить на две взаимно перпендикулярные составляющие, например, на вертикальную составляющую и горизонтальную составляющую.
Таким образом, реакции жесткого защемления А состоят из:
а) реактивного момента МА;
б) горизонтальной составляющей ХА;
в) вертикальной составляющей УА.
2.1. Нахождение реактивного момента МА.
Для нахождения реактивного момента МА мысленно отбрасываем связь, которая препятствует вращению балки АС вокруг точки А, заменяя жесткое защемление новой связью – неподвижным шарниром и прикладывая к ней реактивный момент МА (рис. Д7.4). Таким образом, неизвестную реакцию МА переводим в разряд внешних нагрузок.
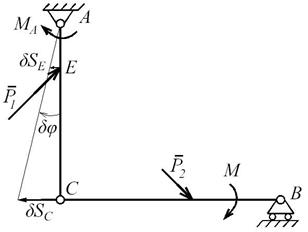
|
На конструкцию действуют сосредоточенные силы  и
и  и моменты М и МА. Связи А (неподвижный шарнир) и В (шарнир подвижный) являются идеальными, поэтому их реакции не входят в уравнение принципа возможных перемещений:
и моменты М и МА. Связи А (неподвижный шарнир) и В (шарнир подвижный) являются идеальными, поэтому их реакции не входят в уравнение принципа возможных перемещений:
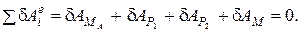 (4)
(4)
Определим значение элементарных работ, входящих в уравнение (4):
а) элементарная работа реактивного момента:

б) элементарная работа силы  :
:
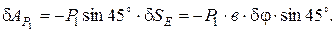
Здесь δ SE - элементарное перемещение точки Е балки АС, к которой приложена сила  ;
;
в) элементарная работа силы  :
:

где δ SС – элементарное перемещение т. С;
г) элементарная работа момента М:

т.к. балка ВС совершает движение без вращения.
Подставляем полученные значения элементарных работ в уравнение (4):
 (5)
(5)
Сокращая обе части уравнения (5) на δφ ≠ 0, найдем искомый реактивный момент:
 кН·м.
кН·м.
2.2. Нахождение горизонтальной составляющей ХА.

|
 отбросим связь, которая препятствует горизонтальному перемещению точки А. С этой целью заменим жесткое защемление ползуном в горизонтальных направляющих, который жестко соединен с балкой АС и приложим к ползуну неизвестную реакцию
отбросим связь, которая препятствует горизонтальному перемещению точки А. С этой целью заменим жесткое защемление ползуном в горизонтальных направляющих, который жестко соединен с балкой АС и приложим к ползуну неизвестную реакцию  (рис. Д7.5). Вследствие замены связи конструкция становится подвижной с одной степенью свободы и вся конструкция может перемещаться поступательно. Дадим системе возможное перемещение δ х, направленное вдоль реакции
(рис. Д7.5). Вследствие замены связи конструкция становится подвижной с одной степенью свободы и вся конструкция может перемещаться поступательно. Дадим системе возможное перемещение δ х, направленное вдоль реакции  и составим уравнение равновесия на основе принципа возможных перемещений (учитываем, что внешние нагрузки в данном случае:
и составим уравнение равновесия на основе принципа возможных перемещений (учитываем, что внешние нагрузки в данном случае:  ,
,  ,
,  и М):
и М):
 (6)
(6)
Вычислим значения элементарных работ, входящих в уравнение (6):
а) элементарная работа силы  :
:

б) элементарная работа силы  :
:

в) элементарная работа силы  :
:

г) элементарная работа момента М:

Работа момента М равна нулю, т.к. балка ВС не совершает вращательного движения.
Следовательно, уравнение (6) примет вид:

Находим искомую реакцию:
 кН.
кН.
Знак «минус» означает, что в действительности реакция  направлена в ту сторону, противоположную той, которая показана на рис. Д7.5.
направлена в ту сторону, противоположную той, которая показана на рис. Д7.5.
2.3. Нахождение вертикальной составляющей УА.
Так же, как и при определении  , для нахождения вертикальной составляющей УА отбросим связь, препятствующую вертикальному перемещению точки А. Для этого заменим связь «жесткое защемление» другой связью – «ползун, жестко связанный с балкой АС, перемещающийся в вертикальных направляющих» и приложим к ползуну неизвестную реакцию
, для нахождения вертикальной составляющей УА отбросим связь, препятствующую вертикальному перемещению точки А. Для этого заменим связь «жесткое защемление» другой связью – «ползун, жестко связанный с балкой АС, перемещающийся в вертикальных направляющих» и приложим к ползуну неизвестную реакцию  (рис. Д7.6).
(рис. Д7.6).
Дадим системе возможное перемещение δ у. При этом балка АС будет совершать поступательное движение, а балка ВС будет вращаться вокруг точки В. Учитывая, что внешние нагрузки в этом случае  ,
,  ,
,  и М, составим уравнение равновесия на базе принципа возможных перемещений:
и М, составим уравнение равновесия на базе принципа возможных перемещений:
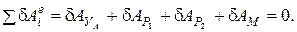 (7)
(7)
Элементарные работы равны:
а) силы  :
:

б) силы  :
:
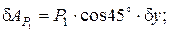
в) силы  :
:
 (8)
(8)
В уравнении (8) учтено, что

г) момента М:

Подставим выражения элементарных работ в уравнение (7):
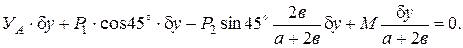
Отсюда:

 кН.
кН.
Знак «минус», как и при нахождении реакции  , означает что действительное направление реакции
, означает что действительное направление реакции  противоположно принятому в наших расчетах.
противоположно принятому в наших расчетах.
Ответ: RB = 15,2 кН; МА = 18,0 кН·м; ХА = -21,2 кН; УА = -10,9 кН.
Дата добавления: 2015-07-11; просмотров: 429 | Нарушение авторских прав