Время движения якоря электромагнита.

Физические процессы в электромагните описываются уравнениями

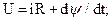
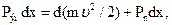
где Рэм − электромагнитная сила, воздействующая на якорь; dx − путь, пройденный якорем; т − масса подвиж­ных частей, приведенная к зазору; v − скорость перемеще­ния якоря, приведенная к зазору; Рn − противодействую­щее усилие пружины, приведенное к зазору.

Вторым уравнением описывается энергетический баланс в электромагните. Работа, произведенная электромагнитом, затрачивается на увеличение кинетической энергии его подвижных частей и преодоление противодействующих сил. Оба эти уравнения нелинейны и их решение затруднительно. В самом общем случае задача решена Н. Е. Лысовым.

Ориентировочно определить время движения якоря мож­но с помощью статической тяговой характеристики. На рис. 5изображены статическая тяговая характеристика элек­тромагнита 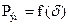и характеристика противодействую­щей силы 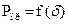. Разность Р_эм − Pпр расходуется на со­общение ускорения подвижным частям электромагнита

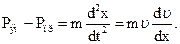(2.7)

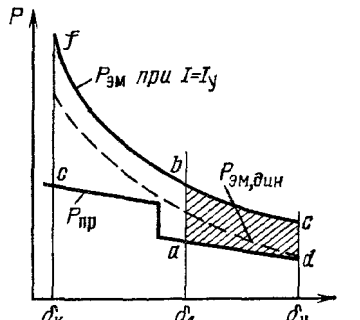
Рисунок 5 – К расчету времени движения якоря

После интегрирования (2.7) получим

(2.8)

Скорость якоря в точке хода, соответствующей зазору ,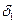

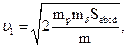
где − масштабы по соответствующим осям; Sabcd − площадь, пропорциональная работе движущей электромагнитной силы.

Зная скорость в любой точке хода, можно рассчитать время движения якоря на всех участках его перемещения.

Если принять участок 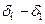за элементарный, то время перемещения по нему якоря

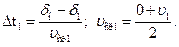
Полное время движения якоря от зазора δ_н до конечного δ_к определяется как сумма элементарных времен:

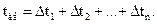(2.9)

Это время меньше действительного, так как статическая тяговая характеристика 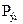располагается выше динами­ческой (рис. 5) .

После остановки якоря ток начнет увеличиваться до тех пор, пока не достигнет установившегося значения I_у = −U/R.При этом Т1>Т, поскольку конечный зазор δ_к меньше начального δ_н, что сказывается на значении L, оп­ределяющем постоянную времени цепи. Так как в притя­нутом положении якоря зазор δ_к мал, то возможно насы­щение магнитной системы. При этом закон нарастания тока может отличаться от экспоненциального, что необходимо учитывать при расчете времени установления потока.

2.3 Отпускание электромагнита.

При размыкании цепи обмотки электромагнита магнитный поток в нем начинает уменьшаться из-за введения в цепь большого сопротивления дугового или тлеющего разряда между контактами. Маг­нитный поток уменьшается, и в момент, когда сила тяги электромагнита становится меньше усилия пружины, проис­ходит отпускание якоря. Время отпускания t_отп состоит из времени спада потока t_сп от установившегося Ф_у до потока отпускания Ф_отп и времени движения t_дв.

Процесс отпускания описывается уравнением

U = iR_д + iR + L_Kdi/dt,

где Rд − сопротивление искры (дуги); L_K − индуктивность цепи обмотки при конечном зазоре.

Если положить, что Rд =const, то решение уравнения примет вид

где 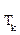− постоянная времени, равная 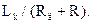Обычно Rд>>R. Тогда

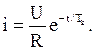
Так как R_д велико, то Т_к очень мало. Процесс спада тока, а, следовательно, и магнитного потока протекает очень быстро. Если сердечник, на котором размещается обмотка, сплошной и имеет большое сечение, то спад магнитного потока замедляется, так как в сердечнике возникают вих­ревые токи, поле которых стремится поддерживать спада­ющий поток. Это необходимо учитывать при рас­чете tсп.

После трогания якоря его движение происходит за счет усилия противодействующей пружины. Если это усилие по­стоянно и равно среднему значению Р_пр,ср = (Р_к+Р_н)/2, где Р_к и Р_н − усилия пружины при зазорах δ_к и δ_н, то движение описывается уравнением

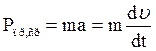
и ускорение

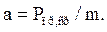
Время движения или

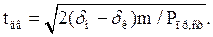(2.10)

III.Напишите выражение для электродинамического усилия, действующего на проводник с током в магнитном поле. Объясните физический смысл входящих параметров.

Расчет электродинамических сил на основании закона взаимодействия проводника с током и магнитным полем. Возьмем систему из двух произвольно расположенных проводников 1 и 2 (рис. 6), обтекаемых токами i₁ и i₂. Напряженность магнитного поля, создаваемого элементом dy проводника 2 в месте расположения элемента dx проводника 1, будет

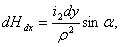
где α — угол между вектором ρ и направлением тока по элементу dy.

Рисунок 6 – Расчет электродинамических сил на основании закона взаимодействия проводника с током и магнитным полем.

Весь проводник 2 создает в месте расположения элемента dx напряженность магнитного поля

Элементарная сила, действующая на элемент dx, обтекаемый током i₁

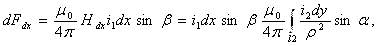
где ρ — угол между вектором магнитной индукции В = μ₀H_dx и вектором тока i₁;

μ₀ ^— магнитная проницаемость воздуха.

Полную силу F взаимодействия между проводниками 1 и 2 получим после интегрирования dF_dx по всей длине проводника 1:

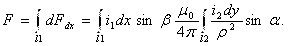
Считая токи i₁ и i₂ неизменными по всей длине проводника, уравнение можно переписать в виде произведения членов:

Первый член этого выражения зависит только от значений токов. Второй член зависит только от взаимного геометрического расположения проводников и представляет собой безразмерную величину. Эту величину часто называют коэффициентом контура, который обозначим буквой с. Тогда

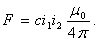
т.е. сила взаимодействия между двумя проводниками, обтекаемыми токами i₁ и i ₂, пропорциональна произведению этих токов (квадрату тока при i₁ = i₂) и зависит от геометрии проводников.

Подставив в уравнение значение μ₀ = 4π10^-7 и вычисляя силу в ньютонах, получим

IV. Задача №1

По индуктивности L=0,4 Гн протекает ток I =10 А. Каково напряжение на индуктивности при разрыве тока (без дуги) и шунтировании ее параллельной емкостью C =0,2 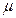Ф. Чему будет равно напряжение, если эту индуктивность шунтировать сопротивлением R=10 Ом?

Дата добавления: 2015-07-11