Построение четырехслойных кривых ВЭЗ

3.1. Построение кривой типа НК (r₁>r₂<r₃>r₄)

Пусть задан следующий разрез:

r₁=1; r₂=1/9; r₃=1; r₄=0.

h₁=1; h₂=2; h₃=12; h₄=¥.

Допустим, что h₃=¥. Тогда, для нанесения верхней части ис­комой кривой можно сразу воспользоваться кривой для n₁=2 из палетки Н–1/9–r₁. Совмещая крест палетки Н–1/9–r₁ с пересечением линий r₁ и h₁ на бланке, переносим кривую А для n₁=2 (рис. 12).

Нанеся верхнюю ветвь искомой кривой, заменим теперь первые два слоя эквивалентным. Точка Н, координаты которой характеризуют сопро­тивление r_1,2 и мощность h_1,2 этого эквивалентного слоя, определит­ся пересечением линии с линией h₁+h₂=3.

Выполнив это построение, получим r_1,2=0,155. Теперь необходимо по­строить трехслойную кривую, соответствующую нижней ветви искомой кривой. Для этой кривой первым слоем будет слой эквивалентный двум слоям искомого разреза, вторым слоем – третий и третьим слоем – четвертый слой искомого разреза, т.е.

r₁=0,155; r₂=1; r₃=0;

h₁=3; h₂=12; h₃=¥.

Для таких соотношений сопротивлений необходимо использовать кривые палеток К для r₃=0. Поскольку в данном случае m₂=r₂/r₁ будет оставлять 6,4, то для нанесения трехслойной кривой следует взять палетки с ближайшими значениями модуля m, т.е. К–9–0 и К–4–0. По принципу эквивалентности Т₂, для этих значений m₂ мы должны взять кривые из палеток для таких значений n₂, чтобы Т₂=m₁n₁=6,4×4=25,6, оставалось постоянным.

Принимая m₂=9 и m₂=4 имеем:

и .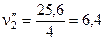

Совмещая крест палетки К–9–0 с точкой Н, переносив путём интерполя­ции между кривыми n=2 и n₂=3 кривую В для n¢₂=2,85.

Таким образом путём интерполяции между кривыми для n₂=5 и n₂=9 переносим на бланк кривую В² для n²₂=6,4 из палатки К–4–0. Далее, интерполируя еще раз между кривыми В и В, окончательно нахо­дим нижнюю ветвь в искомой четырехсложной кривой С, представленной на рис. 12.

В данном примере построение четырехслойной кривой было сравнитель­но облегчено совпадением заданных величин r₂=1/9; n=2 и r₃=1 со значениями, принятыми на палетках. При отсутствии такого совпадения для построения верхней трехслойной кривой пришлось бы осуществить интерполяцию приемами, описанными в разделе построения трехслойных кривых. Если бы также значение r₄ не соответствовало ни одному из имеющихся на палетках значений r₃, то при построении нижней трехслойной кривой необходимо было бы уточнить положение ее конечной асимптоты с помощью палетки «r₂». Для этой цели слой, эквивалентный первым двум слоям заданного разреза (r₁=0,155; h₁=3) и третий слой заданного разреза (r₂=1; h₂=12) необходимо заменить по правилу точки К новым слоем. Для построения точки К надо нанести новые линии.

и h_1,2,3=3+12=15

и от точки Н пересечения отложить отрезок, величина которого при μ₂=6,4 и n₂=4 определяется по диаграмме (рис. 6) в 20 мм. Прикладывая крест палетки «r₂» к точке К мы переносим на бланк кривую для модуля μ равного отношение ρ₄ к абсциссе точки К. Эти кривая и оп­ределит положение конечной асимптоты искомой четырехслойной кривой для заданного ρ₄.

3.2. Построение кривой типа QH (ρ₁>ρ₂>ρ₃<ρ₄)

Кривая задана следующими параметрами:

r₁=1; r₂=0,176; r₃=0,0588; r₄=∞.

h₁=1; h₂=3; h₃=20; h₄=¥.

Положив значение h₃=∞, видим, что первые три слоя представляют собой разрез типа Q, что позволяет построить верхнюю трехслойную кривую заданного четырехслойного разреза как обычную трехслойную кри­вую выше описанным методом (pис. 13).

За начало построения кривой выбираем точку с координатами h₁=1 и ρ₁=1. Определяем модули ρ₂/ρ₁=μ=0,176 и n₁=h₂/h₁=3.

Помещаем точку с координатами h₁ и ρ₁ крест палетки «ρ₂» и переносим с неё на бланк кривую модуля μ=0,176. Это дает начальную ветвь искомой кривой.

Далее заменам первые два слою эквивалентным слоем по правилу точки Q. Для этой цели проведем на бланке линии

и h_1,2=1+3=4.

Пересечение этих линий дает точку Н. Откладывая от этой точки Н по линии S_1,2 вверх отрезок, равный для заданных значений μ и n (согласно рис. 5) 5,5 мм, получим точку Q, координаты которой отвечают сопротивлению ρ₁=0,19 и мощности h₁=3,4 эквивалентного слоя. Это позволяет перейти от четырехслойного разреза снова к трехслойному с параметрами:

r₁=0,19; r₂=0,0588; r₃=∞.

h₁=3,4; h₂=20; h₃=¥.

Этот разрез относится к типу Н. Так как в данном случае

и ,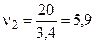

то для построения соответствующей кривой необходимо воспользоваться палетками Н‑1/4‑∞ и Н‑3/7‑∞, предварительно перевычислив значение n₂ для μ равных 1/4 и 3/7. Согласно принципу эквивалентности S₂ при μ'₂=1/4.

при μ''₂=3/7, .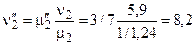

Совмещая последовательно кресты палетки Н‑1/4‑∞ и Н‑3/7‑∞ с точкой Q, переносим на бланк соответствующие кривые В и В''. Искомая кривая проводится методом интерполяции между указанными кривыми.

В этом случае, когда заданное ρ₃ имеет конечное значение, отличное от палеточных, для уточнения положения самой нижней части искомой кривой следует построить дополнительно двухслойную кривую, для которой первым слоем будет слой, эквивалентный первым трем слоям заданного разреза и вторым слоем – четвертый слой заданного разреза. Для этого построения необходимо найти положения точки Н, характеризующей сопротивление и мощность нового эквивалентного слоя. Положение этой точки в данном случае определится пересечением линий:

.

h_1,2,3=3,4+20=23,4.

Совмещая кресс палетки «ρ₂» с точкой Н, следует нанести на бланк кривую с модулем равным отношению заданного ρ₄ к абсциссе точки Н. Эта кривая и будет соответствовать самой нижней асимптоте искомой четырехслойной кривой.

3.3. Построение кривой типа КН (ρ₁<ρ₂>ρ₃<ρ₄)

Построим кривую для следующего разреза:

r₁=1; r₂=5,67; r₃=1,89; r₄=∞.

h₁=1; h₂=3; h₃=20; h₄=¥.

Верхняя часть заданного разреза (при h=¥) относится к типу К для μ'₂=5,67 и n₂=3. Поэтому, для построения верхней трехслойной кривой следует воспользоваться палетками серии К для μ'₂=9 и μ''₂=4. Кроме того, так как значение заданного ρ₃ находится между ρ₃=ρ₁ и для построения должны быть использованы палетки К‑9‑ρ₁, К‑4‑ρ₁, К‑9‑ и К‑4‑ .

По принципу эквивалентности Т₂, заданное μ=5,67 заменяем на μ'₂=9, при этом и на m²₂=4, при этом .

Совмещая крест палетки К‑9‑ρ₁ с пересечением на бланке линий ρ₁ и h₁, переносим кривую А для n=1,9 (рис. 14).Аналогичным образом переносим также кривые из палеток: К‑4‑ρ₁ для n²₂=4,2, К‑9‑ для n²₂=4,2 (кривые А, В и В¢).

Для построения трехслойной кривой, соответствующей нижней части искомой четырехслойной кривой, заменим первые два слоя эквивалентным слоем по правилу точки К. Для этой цели построим линии:

и h_1,2=1+3=4.

От точки пересечения этих линий откладываем вниз по линии S_1,2 отрезок равный для m₂=5,67 и n₂=3 (рис. 6) 20 мм. Это будет точка К, характеризующая сопротивление и мощность эквивалентного слоя.

Теперь следует построить кривую для следующего разреза:

r₁=4,4; r₂=1,89; r₃=∞.

h₁=6,8; h₂=20; h₃=¥.

Этот разрез относится к типу Н с 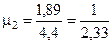и при r₃=¥.

В данном случае значение m₂ соответствует имеющемуся на палетке m₂=3/7, и поэтому, совмещая палетку Н‑3/7‑¥ с точкой К, можно сразу снести кривую С для n₂=3.

Искомая четырехслойная кривая проводится в верхней части путем интерполяции между кривыми А и А¢ и В и В¢ и затем плавно выводится на кривую С.

В случае r₄¹¥, необходимо было бы построить конечную ветвь, пользуясь палеткой «r₂». При этом слои с r_1,2=44 и h_1,2=6,8 и слои r₃=1,89 и h₃=20 следовало бы заменить новым эквивалентным слоем по правилу точки Н.

3.4. Построение кривой типа АК (ρ₁<ρ₂<ρ₃>ρ₄)

Пусть задан следующий четырехслойный разрез:

r₁=1; r₂=4; r₃=16; r₄=0.

h₁=1; h₂=9; h₃=25; h₄=¥.

Первые три слоя представляют собой разрез типа А при m=4, n=9 и r₃=r₂². Следовательно, для построения верхней трехслойной кривой (h₃=¥) можно непосредственно использовать палетку А-4-**. Прикладывая крест этой палетки к точке пересечения на бланке линий r₁=1 и h₁=1, наносим кривую А для n=9 (рис. 15).

Затем заменяем первые два слоя одним эквивалентным слоем по правилу точки А. Для этой цели проведем на бланке линии 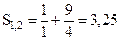, Т_1,2=1×1+9×4=37. Пересечение этих линий определяет положение точки А, координаты которой характеризуют сопротивление (r_1,2) и мощность (h_1,2) эквивалентного слоя.

Это обстоятельство позволяет для построения нижней ветви кривой заданный разрез свести к трехслойному разрезу типа К с параметрами:

r₁=3,4; r₂=16; r₃=0,

h₁=11; h₂=25; h₃=¥

и с модулями и 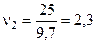и r₃=0.

Заменим по принципу эквивалентности Т₂ величину m=4,7 на m¢₂=4, при этом 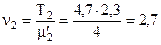и на m²₂=9, при этом .

Совмещая поочередно кресты палеток К-4-0 и К-9-0 с точкой А, перенесем на бланк кривую В для n¢₂=2,7 из палетки К-4-0 и кривую В для построения n²₂=1,2, из палетки К-9-0.

Искомая кривая С при интерполяции между кривыми В и В практически сольется с кривой В. Следовательно, можно было бы ограничиться использованием одной палетки К‑4‑0, так как m¢₂ и n¢₂ мало отличаются от заданных величин m¢₂=4,7 и n₂=2,3.

Если бы заданное r₄¹0, то следовательно бы положение конечной асимптоты искомой кривой уточнить при помощи палетки «r₂», заменив предварительно первый эквивалентный слой и третий слой заданного разреза новым эквивалентным слоем по правилу К.

Литература

1. Каленов Е.И. Интерпретация кривых вертикального электрического зондирования // М.: Гостоптехиздат, 1957. – 472 с.

2. Пылаев А.М. Руководство по интерпретации вертикальных электрического зондирования // М.: Недра, 1968. – 147 с.

3. Смирнов А.А., Закутский С.Н., Притыка И.В. Руководство по обработке и интерпретации результатов наземной электроразведки. Часть 1. Электромагнитное зондирование // Воронеж: изд. ВГУ, 1984. – 232 с.

^

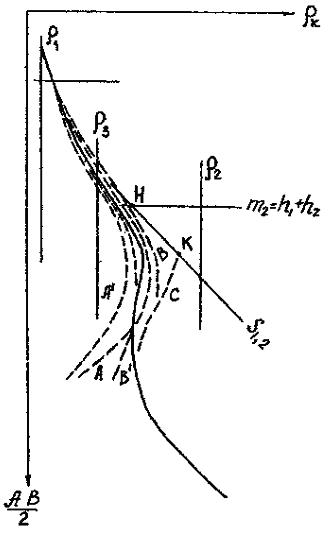
Рис. 14

Рис. 15

Дата добавления: 2015-07-11