Построение трехслойных кривых ВЭЗ

2.1. Построение кривых типа Н (r₁>r₂>r₃)

Теоретически кривые указанного типа характеризуются наличием минимума r_min, отражающего присутствие в разрезе хорошо проводящего второго слоя между менее проводящими слоями.

Пусть для построения кривой типа Н заданы следующие параметры:

r₁=1; r₂=1/10; r₃=3;

h₁=1; h₂=1; h₃=¥.

Отметим на бланке с двойным логарифмическим масштабом точку с абсциссой r_к=r₁=1 и ординатой «АВ/2»=h₁=1 и совместим с этой точкой крест палетки «r₂», сохраняя при этом параллельность соответствующих осей бланка и палетки. После этого перенесём на бланк кривую палетки «r₂» с модулем m=1/9 и m₁=1/19 (рис. 3), осуществляя при этом интерполяцию между двумя кривыми с ближайшими значениями модулей m=1/9 и m₁=1/19. Полученная кривая будет соответствовать на­чальной ветви искомой кривой, на которой еще не сказывается влияние третьего слоя.

Для построения нижней ветви искомой кривой первый и второй слои заменяем одним эквивалентным слоем, для чего на бланк наносим точку Н (Гуммеля), которая для разреза данного типа (r₁>r₂>r₃) явля­ется характерной тачкой, определяющей параметры эквивалентного слоя, т.е. его мощность и сопротивление. Координаты точки Н имеют следующее выражение:

h_1,2=h₁+h₂;

.

где h₁ и r_1,2 соответственно отвечают мощности эквивалентного слоя и его сопротивлению, равному среднему продольному сопротивлению заме­няемых слоев. Следует заметить, что точки Н может быть определено и графически как точки пересечения линий h₁+h₂ и S₁+S₂.

В нашем случае h_1,2=2 и r_1,2=2/11»0,18. Перенесём на бланк точку с абсциссой r_1,2=2/11 и ординатой h₁+h₂=2 и совместим с ней крест палетки r₂. После этого на бланк переносится двухслойная кри­вая с модулем m₂=r₃:r_1,2=3:2/11=16,5. Очевидно, что и в этом слу­чае, ввиду отсутствия на палетке «r₂» кривой для значения r₂=16,5 необходимо проинтерполировать между кривыми с m₂=9 и m₂=19.

Рис. 3

Рис. 4

Нанесенные на бланк двухслойные кривые, определяя положение верхней и нижней части искомой кривой, не дают материала дня нанесения про­межуточной части кривой (минимум r_к), где сказывается называется наличие всех трех слоев.

Для уточнения положения минимума искомой кривой необходимо исполь­зовать трехслойные кривые палетки типа Н. С этой целью из данной серии кривых выбирают такую палетку, параметры которой отвечали бы заданным параметрам разреза. Затем совместим крест искомой кривой с крестом палетки, сопрягают верхнюю и нижнюю ветви по палеточной кривой модуля n=h₂/h₁. Однако, так решается вопрос в принципе, практически же за­данные параметры искомой кривой в полной мере никогда не отвечают па­раметрам теоретических кривых представлены в альбоме, в силу чего сопряжение приобретает несколько более сложный характер.

Так, например, в нашем случае заданные m₁=1/10, а на палетках приняты m=1/19. Это обстоятельство заставляет нас, пользуясь принципом эквивалентности, произвести соответствующий пере­счёт, который сводится к следующему.

Так как , то при заданном m=1/10 будем иметь n¢₁=S₂m¢₁=10×1/9=1,1.

Взяв палетку Н–1/9–r₁, выносим с нее на бланк кривую В₁, для n₁=1,1, осуществляя одновременно интерполирование между кривыми с n₁=1 и n₁=2.

Далее аналогичным образом заменяем заданное m₁ на m₁=1/19, при этом n²₁=S₂m²=10×1/19=0,52»0,5.

Взяв палетку Н – 1/19 – r₁ и накладывая её так, чтобы линии r₁ и h₁ палетки совмещались соответственно с линиями r₁ и h₁ на бланке, наносим на бланк кривую B₂ модуля n=0,5.

В результате интерполяции между двумя нанесенными на бланк кривы­ми B₁ и B₂ мы получим положение минимума трехслойной кривой В для заданного n₁. Как видно из чертежа рис. 3, все три кривые сливаются в одну, что говорит о применимости принципа эквивалентности к заданному разрезу. Но, так как это положение минимума определено для случая r₃=r₃, в то время как заданное r₃=3r₁ то, очевидно, вышеуказанные операции необходимо повторить еще раз с таким расчётом, чтобы по­лучить кривую для заданного n₂, но уже при большем значении r₃=¥.

Напомним только, что с увеличением r₃ пределы принципа эквива­лентности становятся еще более широкими, поэтому достаточно нанести только одну кривую для m=1/9 (ближайшего к заданному), которая бу­дет соответствовать кривым С₁, С₂ и результирующей С для заданных па­раметров, но при r₃=¥.

Искомая трехслойная кривая Д для заданного разреза, совпадая с верхней и нижней части с двухслойными кривыми, в промежуточной части (положение минимума r_к) проводится интерполяцией между кривыми В и С.

Иногда при сопряжении идут по пути упрощения, соединяя верхнюю и нижнюю части искомой кривой плавной линией от руки. Однако следует помнить, что в оценке положения минимума r_к здесь может иметь место большой произвол, особенно тогда, когда верхняя ветвь двухслойной кри­вой пересекается с нижней ветвью под острым углом.

Рис. 5

Рис. 6

В целях более быстрого определения положения точки Н может быть использована палетка LСН (рис. 7). На ней нанесены два семейства кривых, представляющих собою геометрическое место точек H при постоян­ных значениях m₁ и переменных n₁ и постоянных n₁ и переменных ***.

Практически для определения положения точки Н необходимо:

1) совместить крест палетки LCH с точкой на бланке, абсцисса которой равна заданному значению r₁ и ордината – заданному значению h₁;

2) перенести на бланк линию, соответствующую заданному m₁. Пересечение этой линии с ординатой, равной h₁+h₂ определит положе­ние точки Н.

2.2. Построение кривых типа Q (r₁>r₂>r₃)

Методика построения трехслойных кривых типа Q (рис. 4) в значи­тельной степени повторяет методику построения кривых типа Н. Верхняя ветвь искомой кривой строится абсолютно также, как и в предыдущем слу­чае. Для построения нижней ветви отыскивается особая точка, называемая точкой Q, которая характеризует сопротивление и мощность эквивалент­ного слоя. Эмпирически установлено, что точка Q лежит на линии S_1,2, причём она смещена относительно точки Н вверх, в сторону меньших зна­чений АB/2, на некоторую величину. Величина этого смещения, выраженная в миллиметрах (для логарифмического масштаба с модулем 6,25 см), может быть определена по диаграмме, предложенной Мартэном. На этой диаграмме (рис. 5) по оси абсцисс отложены значения m₁=r₂/r₁ по оси ординат – значения n₁=h₂/h₁. Индексы кривых соответствуют величинам смеще­ния точки O от точки Н в мм.

Практически, для определения координат точки Q можно воспользо­ваться палеткой LCQ (рис. 8), на которой даны в виде кривых геометрические места положения точек О (по отношению h и r₁) для постоянных m₁ и переменных n₁, а также для постоянных n₁ и переменных m₁.

Порядок пользования палеткой LСО такой же, как и палеткой LСН.

Положение точки О может быть непосредственно найдено и по формулам, определяющим параметры эквивалентного слоя в условиях разреза типа О.

Эти формулы имеют следующий вид:

и .

Здесь h - некоторый коэффициент, который, как и величина смещения точки О, определяется по диаграмме (рис. 5),

Пример. Требуется построить кривую ВЭЗ для следующего геоэлектрического разреза:

h₁=5 м; h₂=45 м; h₃=¥.

r₁=36 Ом×м; r₂=9 Ом×м; r₃=2 Ом×м;

В целях большого удобства параметры заданного разреза выражаем в отно­сительных единицах (хотя это не обязательно).

h₁=1; h₂=9; h₃=¥.

r₁=1; r₂=1/4; r₃=1/18»0,06;

За начало построения кривой выбираем точку с координатами h₁=1 и r₁=1. Определяем модули m₁=r₂/r₁=1/4 и n₁=h₂/h₁=9. Помещаем в точку с координатами h₁ и r₁ крест палетки «» и переносим с неё на бланк кривую В₁ модуля 1/4. Это дает нам начальную ветвь кривой. Определяем координаты точки О, для чего на бланк наносим точку Н, через которую проводим прямую линию, наклоненную к осям коор­динат под углом 45^о (линия S=S₁+S₂). Согласно диаграмме (рис. 5) точку Н смещаем по линии S_1,2 в сторону меньших АВ/2 на отрезок рав­ный 2 мм (для m=1/4 и n₁=9) и, таким образом, находим точку О, откуда

h_экв=h_1,2=9,7; r_экв=r_1,2=0,26.

Определяем модуль конечной ветви кривой:

m₂=0,06/0,26=0,23.

В точку О помещаем крест палетки «r₂» и на бланк переносим с палетки «r₂» кривую В₂ модуля m₂=0,23. Так как такой кривой на палетке «r₂» нет, поэтому мы указанную кривую наносим путем интерполяции между значениями m₂=1/4 и m₂=1/5.

Соединяем плавной кривой начальную ветвь с конечной; Для более надёжного построения места перегиба кривой наносим из альбома трехслойных кривых две вспомогательных кривые модуля m₁=1/4 и n₂=9 с ближайшим меньшим и большим значениями r₃, помещенные на палетках 0 – 1/4 – 0 и 0 – 1/4 – r₂² (кривые С₁ и С₂).

2.3. Построение кривых типа А (r₁<r₂<r₃)

Методика построения кривых типа А в принципе не отличается от по­строения трехслойных кривых ранее рассмотренных типов. Разница заклю­чается лишь в том, что в данном случае для построения нижней ветви кривой используется особая характерная точка – точка анизотропии А.

Рассмотрим пример графического построения кривой типа А. Пусть мы имеем:

r₁=2 Ом×м; r₂=9 Ом×м; r₃=50 Ом×м;

h₁=3 м; h₂=9 м; h₃=¥.

Отсюда m₁=r₂/r₁=4,5 и n₁=h₂/h₁=3.

S1=h1/r1=4,5	S2=h2/r2=1	S1,2=S1+S2=2,5
T1=h1r1=6	T1=h2r2=81	T1,2=T1+T2=87

Нанесем на бланк точку с абсциссой r₁=2 и ординатой h₁=3. Совмещая с этой точкой крест палетки "r₂", перенесём на бланк кривую r_к(В₁) модуля m₁=4,5 (рис. 10).

Для определения положения точки А нанесем на бланк линии S_1,2 и Т_1,2. Пересечения указанных линий, как известно, дает положение точки А, координаты которой определяют сопротивление r_1,2=5,9 и мощность h_1,2=1,5 эквивалентного слоя. Далее, совмещая крест палетки " " с точкой А, перенесем на бланк кривую (B₂) с m₂=r₃/r_1,2=8,5. Соединяя плавной линией верхнюю и нижнюю части кривых, снятых с палетки "r₂", получаем трехслойную кривую типа А. Однако для нанесения с большей точностью промежуточного участка искомой кривой необходимо ис­пользовать палетки трехслойных кривых типа А. Так как в альбоме пале­ток кривых с заданным модулем m₁=4,5 нет, следует использовать кри­вые с ближайшим m₁=4. В соответствии с этим, заданный параметр n₁, в силу справедливости принципа эквивалентности S₂, примет новое значение:

n¢₂=S₂m=0,67×4=2,68»2,7.

Рис. 7

Рис. 8

Не имея палеток для заданного отношения r₃/r₁, для уточнения положения промежуточной ветви мы вынуждены использовать палетки для ближайших имеющихся значений r₃=r₂/r₁ и r₃=¥. Взяв палетку А–4–r₂² и совмещая линии r₁ и h₁ палетки с линиями r₁ и h₁ на бланке, наносим путём интерполяций кривую С₂ для n¢₁.

Далее с палетки А–4–¥, аналогичным образом наносим на бланк кривую C₂ для n¢₁ и r₃=¥. Интерполируя между этими двумя кривыми, находим местоположение искомой кривой для заданных параметров m₁=4,5; n=3 и r₃=25.

Следует заметить, что координаты точки А, могут быть получены не­посредственно путем расчета по формулам:

и (h₁+h₂)l= .

Кроме того, в целях более быстрого нахождения координат точки А, может быть использована палетка LСА (рис. 7),

На этой палетке даны кривые, соответствующие геометрическим мес­там точек А, как для заданных постоянных значениях m₁ при переменных n₁, так и для постоянных n₁, при переменных m₁. Совмещая крест палетки LCA с крестом искомой кривой, нанесенным на бланк, можно сразу определить положение точки А путём интерполяции между кривыми разных m₁ и n₁.

2.4. Построение кривых типа К (r₁<r₂>r₃)

Построение верхней ветви искомой кривой типа К производится точно также, как и во всех ранее рассмотренных случаях. Построение нижней ветви осуществляется с помощью точки К, определяющей параметры эквива­лентного слоя, т.е. его мощность и сопротивление.

Определение положения точки К может быть выполнено двумя способами.

1-й способ, предложенный М. Мартэном, заключается в том, что в со­ответствии с заданными значениями r₁, h₁, r₂, h₂, строится треугольник анизотропии, составленный линиями S_1,2, T_1,2 и h₁+h₂ (рис. 2). После этого определяется коэффициент анизотропии l, равный высоте треугольника и, согласно графику, представленному на рис. 9, величина поправки e. Откладывая эту величину от точки А вниз, мы по­лучаем положение точки К, характеризующей сопротивление (r_1,2) и мощность (h₁+h₂)le эквивалентного слоя.

Способ А.М. Пылаева проще и состоит в следующем. Сначала наносят на бланк точку Н, лежащую, как уже отмечалось выше, на пересечении ли­ний h₁+h₂ и S_1,2=S₁+S₂. Затем точку Н смещают по линии S_1,2, в сторону больших значений АВ/2 на отрезок, величина которого в мм опре­деляется по специальной диаграмме, представленной на рис. 6.

В ниже приведенном примере построения кривой типа К использован метод А.М. Пылаева.

Рис.9

Рис. 10

Рис. 11

Пусть нам задано:

r₁=1; r₂=15; r₃=1,5;

h₁=1; h₂=1,5; h₃=¥.

Дня построения верхней части искомой кривой помещаем нерест палетки "r₂=" в точку с единичными координатами (r₁=1, h₁=1) и переносим на бланк двухслойную кривую m₁=r₂/r₁=15 (рис. 11).

Построим линию:

S_1,2=S₁+S₂=1+1,5/15=1,1 и h_1,2=h₁+h₂=1+1,5=2.5.

Пересечение этих линий дает положение точки Н. Далее, по диаграмме (рис. 6) определяем для m₁=15 и n₁=1,5 величину смещения точки К от точки Н в 40 мм и, откладывая это расстояние от точки Н по линии S_1,2, определяем положение точки К, характеризующей сопротивление r_1,2=6,5 и мощность h_1,2=1,3 слоя, эквивалентного первым двум слоям.

Положение точки К также может быть определяю с помощью палетки LCK (рис. 8), пользование которой аналогично описанным выше приёмам пользования палетками LCH, LCQ и LCA. Однако при малых значениях m₁, определение положения точки К по диаграмме (рис. 6) оказывается более удобным.

Совмещая крест палетки «r₂» с найденной точкой К, перенесем на бланк двухслойную кривую В с модулем, равным

.

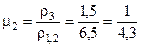Для уточнения промежуточной части кривой (в точке максимума r_к) следует перенести на бланк трехслойные кривые два ближайших, имеющихся на палетке значений m¢₁=19 и m¢₁=9. Кроме того, так как заданное значение r₃/r₁ не подходит к значениям r₃/r₁, имеющимся на палетках, то для возможности интерполяции необходимо перенесение соответствующих кривых как для r₃=r₁, так и для .

По принципу эквивалентности Т₂, при изменении сопротивления вто­рого слоя, его мощность должна измениться таким образом, что величина T₂=h₂r₂=15×1,5=22,5 оставалась постоянной.

Отсюда при m¢₁=19; n¢₁=22,5/19=1,2. И при m²₁=9; n²₁=22,5/9=2,5. Совмещая крест палетки К–19–r₁ с пересечением линий r₁ и h₁ на бланке, переносим на бланк кривую С для n¢₁=1,2, осуществляя при этом интерполирование между кривыми с модулями n₁=1 и n₁=2.

Таким же образом наносится кривая С из палетки К–9–r₁ для n²₁=2,5.

Для данного случая эти кривые отличаются между собой незначитель­но.

Аналогичным образом наносятся кривые D из палетки К–19– для n¢₁=1,2 и кривые D' из палетки К–9– для n²₁=2,5.

Искомая трехслойная кривая проводится в верхней своей части по двухслойной кривой А, в средней части – путём интерполяции между кривыми С и D и, наконец, в нижней части она сливается с двухслойной кривой В.

Рис. 13

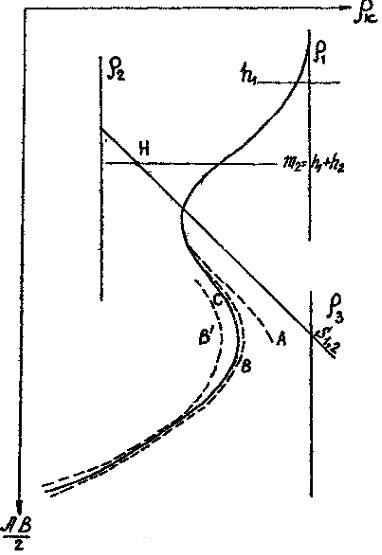
Рис. 12

Дата добавления: 2015-07-11