Особенности лазера для изготовления печатных плат

Возможности увеличения плотности межсоединений в печатных платах непосредственно связаны с литографическими процессами, традиционно завершающимися травлением металлического покрытия (фольги) для формирования токопроводящего рисунка и изоляционных зазоров. На смену стандартной фотолитографии, начинающейся с фотошаблонов, приходят процессы прямого формирования рисунка на фоторезисте (LDI — Laser Direct Imaging), исключающие операцию изготовления фотошаблонов и даже процесс выжигания фольги (или медных покрытий) для обконтуривания проводников изоляционными дорожками. Это позволяет вообще обходиться без процессов фотолитографии и травления.

Самые очевидные преимущества LDI — экономия времени и отсутствие расходов на изготовление, использование, обработку и хранение фотошаблонов. Кроме того, LDI избавлено от проблем, связанных с фотопленкой, ее хранением и дефектами. Процессы LDI обеспечивают лучшую четкость рисунка и позволяют увеличить выход годных печатных плат.

Процессы LDI также обеспечивают более точное совмещение элементов межсоединений, чем методы контактной печати, и поэтому позволяют производить платы самой разнообразной сложности и классов точности. При контактной печати трудно избежать изменений размеров фотошаблонов и деформаций заготовок плат.

Технология LDI помогает избежать всех этих проблем, так как, во-первых, не использует фотошаблонов, и топологическая точность растрового рисунка, сделанного лазерным лучом, не зависит от внешних условий. Во-вторых, большая управляемость, присущая LDI-процессу, позволяет при необходимости изменять размеры, позиционирование и формы элементов рисунка. В итоге, в реальных производственных условиях точность совмещения двух сторон заготовки слоя с размерами 610x812 мм может достигать 24 мкм.

Один из недостатков LDI заключается в невозможности достичь такой же высокой разрешающей способности рисунка, как при контактной печати. Минимальный размер, который могут воспроизвести современные LDI-системы — 25 мкм (15 мкм — для контактной печати). Этот недостаток делает невозможным использование LDI для производства тонких линий,

Есть еще один существенный недостаток LDI — относительно низкая производительность процесса: 80-90 заготовок в час (как для внутренних, так и для внешних слоев). Технология контактной печати позволяет экспонировать порядка 200-300 заготовок в час для внутренних слоев и 90-120 — для внешних.

Производительность LDI-системы может быть улучшена и путем увеличения мощности лазера. Ранее в LDI-системах использовали аргоновые лазеры, например, 4-ваттный аргоновый лазер с длиной волны 351-364 нм.

5. Расчёт основных энергетических, электрических и оптических параметров СО2– лазера.

Расчёт мощности излучения лазера.

Мощность излучения лазера рассчитывается по формуле:

Pmin = P τоптexp(k пог L _с)(1 - ρ)

где τопт– коэффициенты пропускания оптики;

k поги L _с – показатель поглощения и протяженность среды распространения,

ρ – коэффициент отражения объекта облучения.

На основании исходных данных:

Коэффициент пропускания оптики: τопт= 0,7.

Размер зоны облучения: d = 3*10–4м.

Коэффициент отражения объекта облучения: ρ = 0,2

Необходимая облученность объекта W_n = 3*105Вт*м–2.

Скорость перемещения объекта: V = 0.15 м / сек

Найдём площадь зоны облучения за 1 сек:

S = d*V = 3*10–4м * 0.15 м/сек = 4,5*10–5м2 / сек

Значение exp(k пог L _с) примем равным 1, т.к. поглощения воздуха нет.

Pmin = Pобл = Wn*S;

P = Wn*S / τоптexp(k пог L _с)(1 - ρ)

P = ((3*105*4,5*10- 5) / 1*0,7*0,8 = 24,1 Вт

Для обеспечения запаса по излучению увеличим рассчитанное значение P на 29%, тогда

P=24,1+(24,1*0,29) 30Вт

Расчёт параметров активной среды, оптического резонатора и излучения лазера.

Расчёт параметров активной среды.

С помощью программы «LAZER» находим: L AC; d ACи другие параметры лазера.

P 1, Вт/м	λ, мкм	L АС, м	d АС, мм	p, Па	T AC, К
21,7	10,6	1,38	10,33

В приложении представлен график зависимости d AC= ƒ(Р), наглядно демонстрирующий метод линейной аппроксимации для нахождения d AC.

Расчёт параметров плазмы газоразрядных лазеров.

Проектируемый СО2 лазер - газоразрядный лазер тлеющего разряда.

Расчёт электронной температуры Te и продольный градиент потенциала Ez в положительном столбе разряда.

С помощью программы «Laser» при температуре 300 К и суммарном давлении газа 1500 Па получили: Te = 15080 К; Ez = 9756 В/м.

Графики зависимостей Te; Ez от давления представлены в приложении к курсовому проекту.

Расчёт параметров оптического резонатора.

Оптическая длина:

L опт= n L АС= 1*1,38= 1,38м

(для активной среды ГРЛ и воздушных промежутков можно полагать п = 1.)

Анализ устойчивости ОР производится с помощью безразмерных g -параметров:

g 1= 1 – L опт/ R 1, g 2= 1 – L опт/ R 2,

где R 1, R 2– радиусы кривизны зеркал (для плоского зеркала R = ∞).

Условие устойчивости

0 ≤ g 1* g 2≤ 1.

Значения радиусов кривизны сферических зеркал нормированы и составляют на практике 0,5; 1; 1,5; 2; 5 или 10 м.

Согласно найденному значению L опт= 1,38м; R 1= 2 м (берём из нормированных значений) R 2 = ∞, тогда g 1= 0,31 g 2= 1. Исходя из полученных в результате расчётов значений g 1; g 2, можно сделать вывод, что условие устойчивости выполняется.

Расчёт паразитных потерь.

В общем случае для ОР с одинаковыми интерференционными зеркалами(α₁ = α₂₎ и двумя окнами Брюстера можно записать:

α_∑ = α₁ + α₂ = 2(α погл+ α рас+ α ₀+ α Бр+ α д) + α n+ α_β ,

где α погл, α рас– потери на поглощение и рассеяние в отражающих покрытиях;
α₀– потери на зеркалах, обусловленные запылением и загрязнением зеркал;α_Бр– потери излучения при прохождении выходных окон Брюстера; α д– дифракционные потери; α n – потери на границах сред; α_β– потери, обусловленные разъюстировкой зеркал ОР.

Пусть α погл= α рас= 0,5 %, а α₀= 0,4%

В газоразрядных лазерах с внешними зеркалами для уменьшения потерь излучения выходные окна устанавливаются под углом Брюстера:

tg Θ_Бр = n ₁/ n ₀ ≈ n ₁,
где n ₁ и n ₀ – показатели преломления материала выходного окна и воздуха (n ₀ ≈ 1).

В качестве материала выходных окон выберем Германий (Ge) с n ₁ = 4,1 следовательно Θ_Бр = 76º.

Остаточный уровень потерь в окнах Брюстера αБропределяется величиной α₀на каждой из границ раздела сред и поглощением лазерного излучения в материале выходного окна толщиной d = 2...5 мм:

Выберем d = 4 мм; Кпогл = 1.

αБр=2*0,4 + [ 1-exp(-1*4*10- 3/ cos 76)] = 0.817 %

В лазерах дифракция обусловлена ограниченными размерами пучка излучения, циркулирующего в резонаторе. Дифракция происходит на торцах активных элементов и на зеркалах ОР:

NФ = a² / λ L,

где а – диаметр лазерного пучка на зеркале ОР, а = (0,7...0,9)d_АС для ГРЛ

Пусть а = 0,7*10.33, тогда N Ф = 3,57.

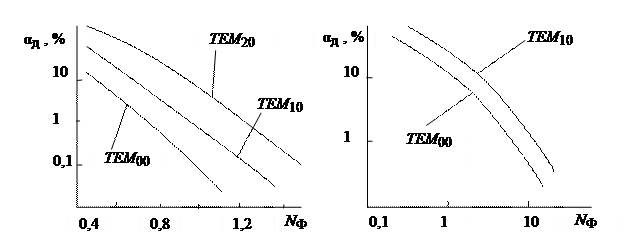
Рис.4. Зависимость дифракционных потерь от числа Френкеля для резонаторов:

а) – конфокального б) – плоского

Строгий расчет a дзатруднителен. На рис.4, представлены результаты приближенного расчета, проведенного на ЭВМ, которыми можно пользоваться для оценки a д.Из рисунка видно, что потери возрастают при переходе от конфокального резонатора к плоскому резонатору, а также с увеличением индексов т и п поперечных мод.

В результате графического анализа коэффициент дифракционных потерь:

a д = 7,5 %.

Дополнительные потери возникают при пересечении лучом границы двух сред с различными показателями преломления. Френелевский коэффициент отражения:

где n 1, n 2– показатели преломления контактирующих сред.

ρ_Ф = 0,3694 (где n 1=1 – воздух, n 2= 4,1 – Ge)

При дополнительном загрязнении границ раздела (торцов элементов и т. п.) α n = ρ_Ф + α ₀;

α n = 0,77

Потери излучения α_β, обусловленные разъюстировкой резонатора, т. е. перекосом зеркал:

Достаточно выбрать значение α_β в пределах 0,5...0,8%

Выберем α_β = 0,5%, после расчётов угол разъюстировки β = 1,87*10^-7.

После расчёта составляющих потерь, α_∑ = 20,7 % α₁ = α₂ = 10,35.

Расчёт оптимального коэффициента пропускания рабочего зеркала.

Определение τ_opt проводиться графически путем построения и поиска максимума функции:

Оптические характеристики активной среды.

Параметр	λ, мкм	κ0,м^–1	κ погл, м^–1	α1,α2, %	τ2, %	п	ΔνАС, ГГц	t2, c
СО2-лазер	10,6	0,8…1,2	0	5...12	10...30	1	0,06	10-3

Оптимальный коэффициент определяем с помощью программы «Win_rk1»:

α₁ = α₂ = 10,35

Пусть κ₀ = 0,8 м^–1

τ_opt = 31,8%. = τ₂ .

График определения τ_opt представлен в приложении.

Выбор и расчёт интерференционных покрытий и подложек зеркал.

В качестве материалов интерференционных покрытий выберем ZnS с высоким коэффициентом преломления и Na₃AlF₆ c низким коэффициентом преломления, материалом подложки будет служить GaAs.

n_ZnS =n_B = 2,3

n_Na3AlF6 = n_н = 1,35

n_GaAs = 4 = n_s

Показатель преломления воздуха n ₀ = 1.

Выражения для максимальных коэффициентов отражения многослойных покрытий:

Для нечетного числа слоев для четного числа слоев

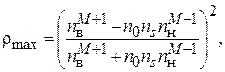
где n_S – показатель преломления материала подложки;
материалы с высоким n ви низким n нпоказателями преломления.

С помощью программы Mathcad строим зависимости Pmax от М:

для нечётного числа слоёв:

для нечётного числа слоёв:

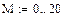
Пропускание, которое обеспечивает рабочее зеркало при данных условиях,
находится как τ = 1 – ρmax.

ρmax = 1 - 0,318 = 0,682.

При нечётном: М = 5 (число слоёв рабочего зеркала).

Для «глухого» зеркала τ = 0; Pmax = 0,998 (такой у лучших образцов).

При чётном М = 18 (число слоёв «глухого» зеркала).

Максимальный коэффициент отражения ρmaxмногослойного покрытия из М слоев реализуется при строгом равенстве оптических толщин слоев четверти длины волны рабочего излучения:

nвdв= nнdн= λ /4,

где d в, d н– геометрические толщины слоев с высоким и с низким показателями преломления.

Величины d в = 1,15 мкм и d н = 1,96 мкм.

Расчёт инверсии населенности лазерных уровней.

Для расчёта стационарной (пороговой) инверсии населенностей Δ n = (n 2– n 1)стлазерных уровней, можно воспользоваться условием стационарной генерации

κ погл = 0 м^–1; L AC= 1,38 м;

ρ₁ = 1 – α₁ – τ₁ и ρ₂ = 1 – α₂ – τ₂ – коэффициенты отражения нерабочего, “глухого” и рабочего зеркал (τ₁ ≈ 0 – коэффициент пропускания “глухого” зеркала; α₁, α₂ – паразитные потери).
τ₂ = 31,18%

ρ₁ = 0,9; ρ₂ = 0,58.

К_ст = 0,236 (коэффициент стационарного усиления)

Вторым соотношением коэффициентов Эйнштейна для спонтанного A₂₁ и индуцированного B₂₁ излучений:

где A ₂₁= t ₂^–1 – вероятность спонтанных переходов частицы (t 2– время жизни верхнего уровня),
t 2= 10-3 с (согласно табл. 3.4 [1]; A₂₁= 1000

B ₂₁ = 7,15*1019

и выражением для насыщенного показателя усиления:

Δν_АС = 0.06 ГГц – спектральная ширина контура усиления активной среды.

h = 6,62*10-34Дж*с – постоянная Планка.

Из выражения находим Δ n = (n 2– n 1)ст = 3,168*1015

Расчёт частотных характеристик лазера.

Важным параметром оптического резонатора является добротность Q, характеризующая его собственные резонансные свойства. Добротность рассчитывается:

где α_∑ = α₁ + α₂; τ_∑ = τ₁ + τ₂ – суммарное пропускание зеркал (для металлических отражающих покрытий τ₁ = 0)

α_∑ = 20,7; τ₁ = 0, τ₂ = 0,318; τ_∑ = 0,318.

С помощью программы «Laser» определяем значение добротности

(график представлен в приложении).

Q =1,56*106.

Ширина собственной резонансной линии пассивного ОР в масштабе частот или длин волн:

Δν_ОР = ν/Q, Δλ_ОР = λ /Q,

где ν = с / λ – частота генерируемой моды, ν =2,83*1013Гц,

Δν_ОР = 1,81*107 Гц; Δλ_ОР =6,8*10-12 м

Помещение в резонатор усиливающей активной среды компенсирует потери и сужает ширину спектральной линии, генерируемой лазером:

где h = 6,62·10–34Дж·с – постоянная Планка; Р – мощность генерации лазера.

∆ν_ф = 5,15*10-6 Гц

Спектр излучения лазера включает продольные и поперечные типы колебаний. Для оценки возможного числа продольных мод зону генерации в первом приближении можно принять равной ширине контура усиления Δν_АС активной среды:

где Δν q = c /2 L опт– интервал частот между соседними продольными модами

Δν q = 10,8*107Гц, N_{пр. мод} = 0,556

Наличие поперечных мод приводит наряду с нарушением однородности распределения интенсивности в пучке к частотным сдвигам относительно основного продольного колебания. Результирующая частота колебания

с продольным индексом q и поперечными индексами т и п определяется как:

Δν_mnq = ν_mnq – ν_00q

В результате расчёта получаем:

∆ν00q = 0 Гц;

∆ν10q = 7,56*106Гц; ∆ν11q = 15,12*106Гц

Расчёт КПД лазера.

Общий КПД любого лазера может быть найден как

где η_нак – КПД накачки, определяющий долю мощности накачки, затраченную на возбуждение АС;

η_АС – КПД активной среды, показывающий, какая доля мощности возбуждения АС преобразовывается в излучение когерентных квантов; η_ОР – КПД оптического резонатора, устанавливающий соотношение между выходной мощностью излучения лазера и мощностью излучения когерентных квантов, циркулирующих в резонаторе.

Расчёт КПД накачки.

КПД накачки ГРЛ может быть определен как

где η_эл – электрический КПД ГРЛ, учитывающий потери мощности в приэлектродных областях разрядной трубки;

η_геом – геометрический КПД, определяемый потерями мощности в зонах положительного столба разряда, не участвующих в процессе усиления АС, например в электродных отростках прибора; η _е – электронный КПД, отражающий долю энергии электронов ПС, расходуемую на возбуждение верхних лазерных уровней.

.

Для приборов тлеющего разряда с холодным катодом (СО2 лазер) значение U _к определяется родом материала катода и наполняющего газа.

Берём газ азот и материал катода - никель, U _к = 200 В,

следовательно: η_эл = 98,53%.

Типичные значения η_геом = 80…95%, возьмём η_геом =85%.

Электронный КПД:

,

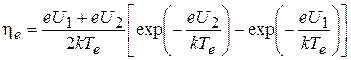где eU ₁, eU ₂ – энергии электронов, нижней и верхней границам зоны возбуждения АС, Дж;

е = 1,6·10^–19 Кл – заряд элекрона; k = 1,38·10^–23 Дж·К^–1 – постоянная Больцмана.

Расчёт производим с помощью программы «Laser»:

η _е = 56%.

В итоге КПД накачки:

η_нак = 47 %.

Графики зависимостей η _е; η_эл от давления представлены в приложении.

Расчёт КПД активной среды и КПД оптического резонатора.

Значение η_АС ГРЛ определяет долю энергии возбуждения, полученную активной средой от электронов и превращаемую АС в энергию когерентных квантов.

η_АС = qW_изл /W_возб, где W_изл = hc/λ.

h = 6,62·10–34Дж·с – постоянная Планка; c – скорость света 3*108; λ = 10,6 мкм.

Коэффициент q = 0,6...0,8 – аналог квантового выхода АС ТТЛ, учитывающий в ГРЛ потери энергии возбуждения за счет спонтанных и безызлучательных переходов с верхних лазерных уровней.

Выберем q = 0,8; W_изл = 1,87*10-20Дж; W_возб ≈ 0,3 Эв = 4,806*10-20Дж.

η_АС = 38,9%.

КПД оптического резонатора ГРЛ определяется по формуле:

η_ОР = τ₂/(α₁ + α₂ + τ₁ + τ₂),
где τ₁ ≈ 0 – коэффициент пропускания “глухого” зеркала;

τ₂ = 31,8% – коэффициент пропускания рабочего зеркала;

α₁, α₂ = 10,35 % – паразитные потери.

В результате расчёта получим η_ОР = 60,57%.

В итоге полный КПД:

= 11%.

Расчёт энергетических и электрических параметров лазера.

Расчёт мощности накачки.

Мощность накачки лазера непрерывного режима определяется по формуле:

;

где Р_{пор АС}– пороговая мощность возбуждения активной среды лазера.

Пороговая энергия возбуждения АС:

W_порАС = A nV W_возб,

где A – минимальная от общего числа доля возбуждения частиц;
n– концентрация частиц в АС; V – объем активной среды.

V = L AC* π(d AC/2)² = 1,38*3,14(0,0103/2)² = 1,15*10-4м3

А = 1*10–2

Для ГРЛ значения n рассчитываются исходя из ранее найденного давления активной газовой среды (р = nkT_АС).

k = 1,38·10^–23 Дж·К^–1 – постоянная Больцмана; р = 1500 Па; T_АС = 300…350 К.

Выберем значение T_АС = 300 К.

n = p/ T_АС*k = 1500 / 300*1,38·10^–23 = 3,62*10²³

W_возб ≈ 0,3 Эв = 4,806*10-20Дж.

W_порАС = 0,02 Дж

t₂ ,с = 10–3

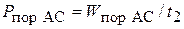= 20 Вт

η_нак = 47 %; η_О = 11 %; P = 30 Вт

Рн = 315,3 Вт

Дата добавления: 2015-07-11