
|
Читайте также: |
Кривые второго порядка
Определение 30. Кривой второго порядка называется кривая, задающаяся в некоторой прямоугольной системе координат 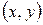 уравнением
уравнением
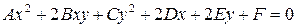 , ,
| (53) |
где А, В, С, D, E, F — действительные числа, причём А, В, С одновременно не равны нулю. ٱ
В случае, когда не существует точек 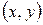 с действительными координатами, удовлетворяющих уравнению (53), говорят, что уравнение (53) определяет мнимую кривую второго порядка. Примером такого уравнения может служить уравнение
с действительными координатами, удовлетворяющих уравнению (53), говорят, что уравнение (53) определяет мнимую кривую второго порядка. Примером такого уравнения может служить уравнение 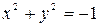 . Мы не будем рассматривать ни мнимые кривые, ни другие «вырожденные» случаи уравнения (53), как например:
. Мы не будем рассматривать ни мнимые кривые, ни другие «вырожденные» случаи уравнения (53), как например:
а) уравнение пары пересекающихся прямых: 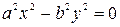
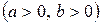 ;
;
б) уравнение пары параллельных или совпадающих прямых: 
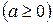 ;
;
в) уравнение, определяющее точку: 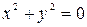 .
.
Выделяют три основных нетривиальных случая общего уравнения (53).
1) Уравнение эллипса
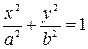 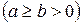
| (54) |
с полуосями длины а и b. В частности, при 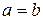 получаем уравнение окружности
получаем уравнение окружности 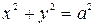 с центром в начале координат и радиусом а.
с центром в начале координат и радиусом а.
2) Уравнение гиперболы
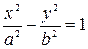 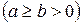
| (55) |
с полуосями а и b.
3) Уравнение параболы
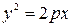 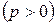 . .
| (56) |
Уравнения (54)–(56) называются каноническими. Остановимся подробнее на перечисленных кривых.
Эллипс
Определение 31. Пусть на плоскости заданы точки 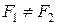 . Эллипсом с фокусами
. Эллипсом с фокусами 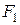 и
и 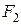 называется геометрическое место точек
называется геометрическое место точек 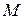 данной плоскости, отличных от точек
данной плоскости, отличных от точек 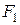 и
и 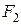 и таких, что сумма расстояний от
и таких, что сумма расстояний от 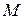 до
до 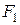 и от
и от 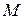 до
до 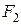 постоянна и равна 2а.
постоянна и равна 2а.
| ٱ |
Имея в виду определение 31, зададим прямоугольную систему координат следующим образом. В качестве оси абсцисс выберем прямую, проходящую через точки 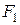 и
и 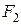 ; начало координат
; начало координат 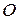 поместим в середину отрезка, соединяющего
поместим в середину отрезка, соединяющего 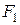 и
и 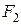 ; осью
; осью 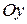 назначим прямую, проходящую через точку
назначим прямую, проходящую через точку 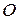 , перпендикулярно к оси
, перпендикулярно к оси 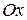 . Ясно, что
. Ясно, что 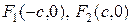 , где
, где 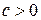 — некоторое число. Тогда точки
— некоторое число. Тогда точки 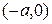 и
и 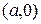 удовлетворяют определению 31 (т.е. принадлежат эллипсу), причем
удовлетворяют определению 31 (т.е. принадлежат эллипсу), причем 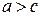 (докажите это!). Обозначим
(докажите это!). Обозначим 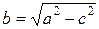 . Покажем, что уравнение (54) действительно является уравнением
. Покажем, что уравнение (54) действительно является уравнением
эллипса в смысле определения 31.
Пусть 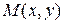 — произвольная точка эллипса. Имеем:
— произвольная точка эллипса. Имеем:
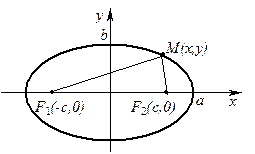
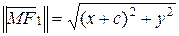 ,
, 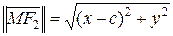 . По определению эллипса должно выполняться условие
. По определению эллипса должно выполняться условие 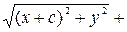
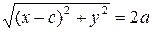 . Проведём выкладки, приводящие это уравнение к виду (54). Действительно,
. Проведём выкладки, приводящие это уравнение к виду (54). Действительно,
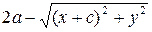 =
= 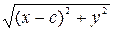
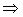
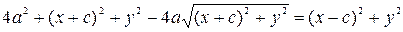
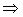
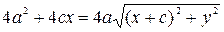
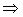
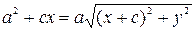
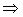
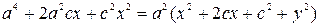
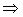
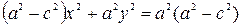
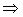
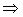 (54).
(54).
Проследив эти выкладки в обратном порядке, можно показать, что для произвольной точки 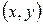 , удовлетворяющей уравнению (54), сумма расстояний от неё до
, удовлетворяющей уравнению (54), сумма расстояний от неё до 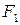 и
и 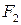 равна
равна 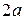 (докажите это!).
(докажите это!).
Точки пересечения эллипса с координатными осями называются вершинами эллипса, а отрезки, заключённые между вершинами, называются осями эллипса: большая (фокальная) ось длиной 2а и малая ось длиной 2b. Оси координат являются осями симметрии эллипса, а начало координат — его центром симметрии. Легко понять, что окружность является частным случаем эллипса (фокусы при этом совпадают и служат центром окружности).
 Для построения эллипса нарисуем две концентрические окружности радиусов b и а
Для построения эллипса нарисуем две концентрические окружности радиусов b и а 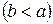 с центром в точке О. Затем из точки О проведем луч под углом
с центром в точке О. Затем из точки О проведем луч под углом 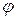 к оси Ох и обозначим его точки пересечения с окружностями радиусов b и а, соответственно, Т и N. Из точки N проведём прямую, параллельную оси Оу, а из точки Т — прямую, параллельную оси Ох. Точка пересечения М этих прямых имеет координаты
к оси Ох и обозначим его точки пересечения с окружностями радиусов b и а, соответственно, Т и N. Из точки N проведём прямую, параллельную оси Оу, а из точки Т — прямую, параллельную оси Ох. Точка пересечения М этих прямых имеет координаты
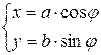 , , 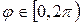 , ,
| (57) |
Так как 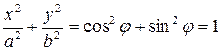 , то точка М принадлежит эллипсу. Легко понять, что точки, задающиеся уравнениями (57), покрывают весь эллипс (докажите это!).
, то точка М принадлежит эллипсу. Легко понять, что точки, задающиеся уравнениями (57), покрывают весь эллипс (докажите это!).
Гипербола
Определение 32. Пусть на плоскости заданы точки 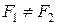 . Гиперболой с фокусами
. Гиперболой с фокусами 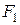 и
и 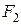 называется геометрическое место точек
называется геометрическое место точек 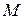 данной плоскости, отличных от точек
данной плоскости, отличных от точек 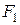 и
и 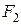 и таких, что
и таких, что 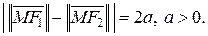 ٱ
ٱ
Введем декартову систему координат точно так же, как это делалось при рассмотрении эллипса. Таким образом, 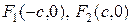 , где
, где 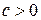 — некоторое число, и точки
— некоторое число, и точки 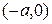 и
и 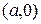 удовлетворяют определению 32 (т.е. принадлежат гиперболе), причем
удовлетворяют определению 32 (т.е. принадлежат гиперболе), причем 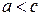 (докажите это!). Обозначим
(докажите это!). Обозначим 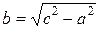 . Покажем, что уравнение (55) действительно является уравнением гиперболы в смысле определения 32.
. Покажем, что уравнение (55) действительно является уравнением гиперболы в смысле определения 32.
Пусть 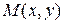 — произвольная точка гиперболы. Имеем:
— произвольная точка гиперболы. Имеем:
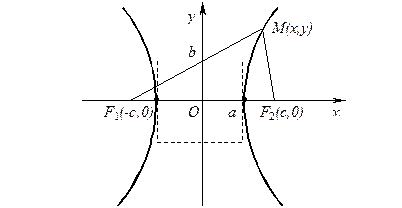
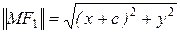 ,
, 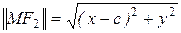 .
.
Из определения 32 следует:
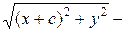
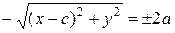
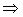
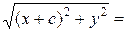
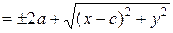
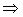
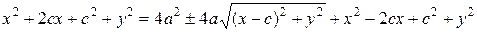
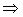
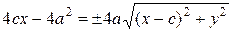
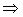
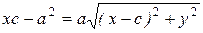
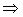
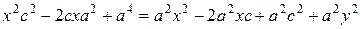
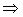
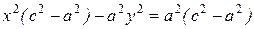
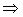
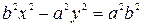
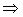 (55).
(55).
Проследив эти выкладки в обратном порядке, можно показать, что для произвольной точки 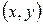 , удовлетворяющей уравнению (55), модуль разности расстояний от неё до
, удовлетворяющей уравнению (55), модуль разности расстояний от неё до 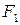 и
и 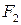 равен
равен 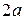 (докажите это!).
(докажите это!).
Точки пересечения 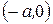 и
и 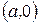 гиперболы с осью Ох называются вершинами гиперболы, а величина а — действительной полуосью. Точки
гиперболы с осью Ох называются вершинами гиперболы, а величина а — действительной полуосью. Точки 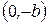 и
и 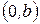 называются мнимыми вершинами гиперболы, а величина b — мнимой полуосью. Прямоугольник с центром в начале координат и со сторонами, параллельными координатным осям и проходящими через вершины параболы, называется основным прямоугольником гиперболы. Его диагонали
называются мнимыми вершинами гиперболы, а величина b — мнимой полуосью. Прямоугольник с центром в начале координат и со сторонами, параллельными координатным осям и проходящими через вершины параболы, называется основным прямоугольником гиперболы. Его диагонали 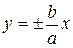 являются асимптотами гиперболы. Оси координат являются осями симметрии гиперболы, а начало координат — её центром симметрии. Если
являются асимптотами гиперболы. Оси координат являются осями симметрии гиперболы, а начало координат — её центром симметрии. Если 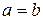 , то гипербола называется равносторонней.
, то гипербола называется равносторонней.
Парабола
Определение 33. Пусть на плоскости задана прямая 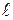 и точка
и точка 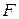 , не лежащая на этой прямой. Параболой называется геометрическое место точек
, не лежащая на этой прямой. Параболой называется геометрическое место точек 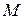 плоскости, равноудалённых от данной точки
плоскости, равноудалённых от данной точки 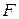 (фокуса) и от данной прямой
(фокуса) и от данной прямой 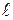 (директрисы). ٱ
(директрисы). ٱ
Если за ось абсцисс принять прямую, проходящую через фокус и перпендикулярную директрисе, а начало координат поместить посередине между фокусом и директрисой, то уравнение параболы примет вид (56).
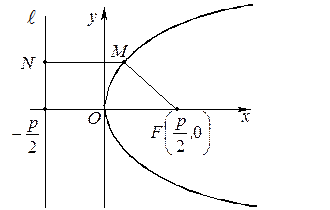 Действительно, введем
Действительно, введем  такое, что
такое, что 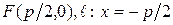 ; обозначим через N проекцию точки
; обозначим через N проекцию точки 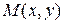 на директрису. Тогда
на директрису. Тогда
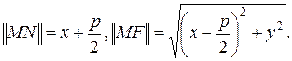 По определению 33:
По определению 33:
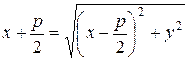
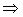
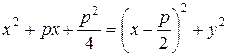
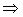
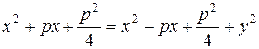
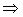 (56).
(56).
Парабола имеет одну ось симметрии, которая при указанном выше выборе системы координат совпадает с осью Ох. Точка 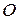 является вершиной параболы.
является вершиной параболы.
В конкретных примерах часто встречаются параболы вида: (а) 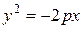 ,
,
(б) 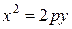 и (в)
и (в) 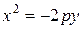 . Представленные уравнения описывают различные положения параболы в системе координат, характеризующиеся направлением ветвей параболы. Так ветви параболы, заданной уравнением (а) симметричны относительно оси Ох, но направлены в отрицательную сторону этой оси. Уравнения (б) и (в) задают параболы, ветви которых симметричны относительно оси Oy и имеют в случае (б) положительное, а в случае (в) отрицательное направления. При этом уравнения директрис и координаты фокусов для каждого представленного варианта легко находятся. Вершины парабол во всех перечисленных случаях совпадают с началом координат.
. Представленные уравнения описывают различные положения параболы в системе координат, характеризующиеся направлением ветвей параболы. Так ветви параболы, заданной уравнением (а) симметричны относительно оси Ох, но направлены в отрицательную сторону этой оси. Уравнения (б) и (в) задают параболы, ветви которых симметричны относительно оси Oy и имеют в случае (б) положительное, а в случае (в) отрицательное направления. При этом уравнения директрис и координаты фокусов для каждого представленного варианта легко находятся. Вершины парабол во всех перечисленных случаях совпадают с началом координат.
Лекция 14
Приведение общего уравнения второго порядка к каноническому виду
Замечание. В последующем изложении уравнения (54)–(56) мы будем называть каноническими также в случаях, когда 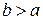 или
или 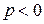 .
.
Когда уравнение носит название «каноническое», то имеется в виду особое положение линии на плоскости относительно определённой там системы координат. Если же вводится новая система координат, то вид уравнения той же линии может существенно измениться.
Простейшим преобразованием прямоугольной системы координат на плоскости является параллельный перенос. Расмотрим новую систему 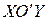 , полученную сдвигом старой системы хОy на вектор
, полученную сдвигом старой системы хОy на вектор 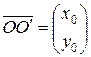 .
.  Ясно, что точка
Ясно, что точка 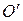 — начало новой системы координат — имеет в старой системе координаты (х 0, у 0). Выясним связь между координатами произвольной точки
— начало новой системы координат — имеет в старой системе координаты (х 0, у 0). Выясним связь между координатами произвольной точки 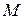 в этих системах. Легко видеть, что координаты (х, у) точки
в этих системах. Легко видеть, что координаты (х, у) точки 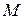 в старой системе координат и координаты (Х, Y)этой точки в новой системе координат связаны соотношениями:
в старой системе координат и координаты (Х, Y)этой точки в новой системе координат связаны соотношениями:
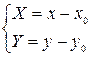 . .
| (58) |
С помощью преобразования (58) можно приводить к каноническому виду уравнение (53) в случае, когда 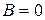 , то есть когда это уравнение принимает вид:
, то есть когда это уравнение принимает вид:
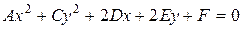 . .
| (59) |
Данное уравнение преобразуется к каноническому виду выделением полных квадратов с последующим параллельным переносом по формулам (58).
Пример 32. Привести к каноническому виду уравнение линии второго порядка 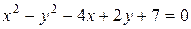 . Определить вид и расположение этой линии, найти координаты её фокусов.
. Определить вид и расположение этой линии, найти координаты её фокусов.
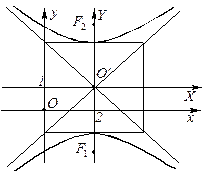 Выделим сначала полные квадраты при х и при у:
Выделим сначала полные квадраты при х и при у: 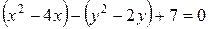
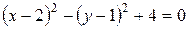 . Перейдем к новой системе координат:
. Перейдем к новой системе координат: 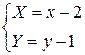 . Новая система получается из старой системы координат сдвигом на вектор
. Новая система получается из старой системы координат сдвигом на вектор 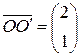 . В новых координатах получим
. В новых координатах получим 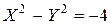
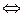
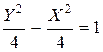 . Это уравнение гиперболы. Так как её полуоси
. Это уравнение гиперболы. Так как её полуоси 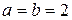 , то это равносторонняя гипербола, действительная ось которой совпадает с осью
, то это равносторонняя гипербола, действительная ось которой совпадает с осью  . На этой же оси также расположены фокусы
. На этой же оси также расположены фокусы 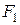 и
и 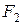 , отстоящие от центра
, отстоящие от центра 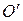 на расстоянии
на расстоянии 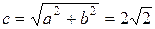 .
.
Более сложным преобразованием координат является поворот старой системы вокруг своего начала  (см. лекцию 7, пример 15). Пусть в уравнении (53)
(см. лекцию 7, пример 15). Пусть в уравнении (53) 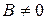 . Тогда общее уравнение кривой (53) преобразуется к виду (59) с помощью поворота координатных осей на угол
. Тогда общее уравнение кривой (53) преобразуется к виду (59) с помощью поворота координатных осей на угол 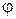 по формулам:
по формулам:
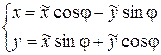 , (60) , (60)
|
где, как нетрудно доказать, 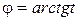 можно найти, используя один из корней уравнения
можно найти, используя один из корней уравнения
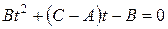 . .
| (61) |
При этом числа 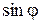 и
и 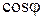 находятся по формулам:
находятся по формулам:
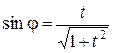 , , 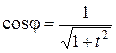 . .
| (62) |
Уравнение второй степени называется эллиптическим, если  ; гиперболическим, если
; гиперболическим, если 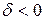 ; параболическим, если
; параболическим, если 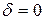 . Если в уравнении (53) величина
. Если в уравнении (53) величина 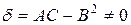 , то данное уравнение определяет центральную линию второго порядка, то есть линию, имеющую центр симметрии (эллипс, гиперболу).
, то данное уравнение определяет центральную линию второго порядка, то есть линию, имеющую центр симметрии (эллипс, гиперболу).
Пример 33. Привести к каноническому виду уравнение кривой второго порядка 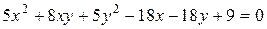 .
.
 Из уравнения (61) находим угол, на который нужно повернуть исходную систему координат, чтобы в данном уравнении в новых осях пропало слагаемое с произведением координат:
Из уравнения (61) находим угол, на который нужно повернуть исходную систему координат, чтобы в данном уравнении в новых осях пропало слагаемое с произведением координат: 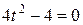
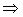
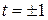 . Возьмем корень
. Возьмем корень 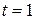 . Тогда
. Тогда 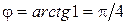 , то есть формулы преобразования координат (60) примут вид:
, то есть формулы преобразования координат (60) примут вид: 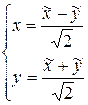 . Исходное уравнение преобразуется к виду:
. Исходное уравнение преобразуется к виду:
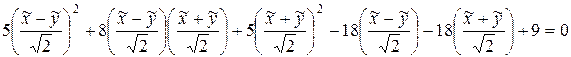
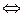
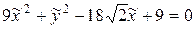
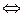
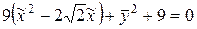 .
.
Продолжим преобразования. Выделяя при 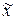 полный квадрат, получим:
полный квадрат, получим:
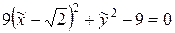
 .
.
Данное уравнение ещё не является каноническим: необходимо осуществить параллельный перенос системы координат  , полученной из исходной поворотом на угол
, полученной из исходной поворотом на угол 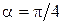 . По формулам (58) связь между системами
. По формулам (58) связь между системами 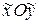 и
и 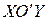 выражается следующим образом:
выражается следующим образом: 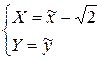 . Это означает, что система
. Это означает, что система 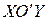 получается параллельным переносом системы
получается параллельным переносом системы 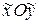 на вектор
на вектор 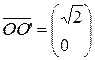 . В системе
. В системе 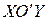 наше уравнение принимает вид:
наше уравнение принимает вид: 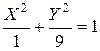 . Это каноническое уравнение эллипса с полуосями
. Это каноническое уравнение эллипса с полуосями 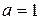 и
и 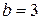 .
.
Замечание. Нетрудно доказать, что уравнение (53) всегда можно привести к каноническому виду с помощью преобразований поворота и сдвига исходной системы координат.
Полярная система координат
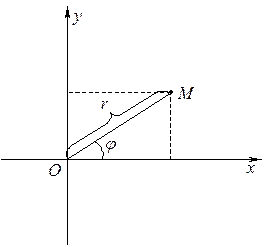 Помимо прямоугольной системы координат положение произвольной точки
Помимо прямоугольной системы координат положение произвольной точки 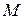 на плоскости можно определить при помощи так называемой полярной системы координат. Рассмотрим луч
на плоскости можно определить при помощи так называемой полярной системы координат. Рассмотрим луч 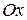 , который будем называть полярной осью. Начало луча О называется полюсом. Положение точки М однозначно определяется парой чисел
, который будем называть полярной осью. Начало луча О называется полюсом. Положение точки М однозначно определяется парой чисел 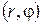 , где
, где 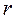 — расстояние от полюса О до М и
— расстояние от полюса О до М и 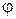 — угол, отсчитываемый от полярной оси против часовой стрелки до направления ОМ. Эти числа называются полярными координатами точки М. По определению величина
— угол, отсчитываемый от полярной оси против часовой стрелки до направления ОМ. Эти числа называются полярными координатами точки М. По определению величина 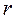 не отрицательна.
не отрицательна.
Если ограничить изменение угла 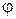 пределами
пределами 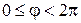 , то каждой точке
, то каждой точке 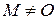 плоскости однозначно отвечает пара чисел
плоскости однозначно отвечает пара чисел 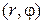 . Исключение составляет полюс О: для него
. Исключение составляет полюс О: для него 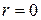 , а угол
, а угол 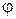 неопределен.
неопределен.
Ясно, что связь между декартовыми и полярными координатами осуществляется формулами:
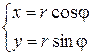 . .
| (63) |
Цилиндрическая система координат
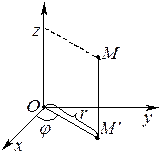 Принцип, по которому вводилась полярная система координат на плоскости, послужил основой для введения в пространстве
Принцип, по которому вводилась полярная система координат на плоскости, послужил основой для введения в пространстве  цилиндрической системы координат. Цилиндрические координаты точки
цилиндрической системы координат. Цилиндрические координаты точки  в пространстве — это тройка чисел
в пространстве — это тройка чисел 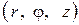 , где
, где 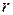 и
и 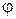 имеют ту же интерпретацию, что и в полярной системе координат, только для проекции точки
имеют ту же интерпретацию, что и в полярной системе координат, только для проекции точки 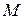 пространства на плоскость хОу. Таким образом, в цилиндрических координатах положение произвольной точки пространства М определяется: расстоянием от её проекции
пространства на плоскость хОу. Таким образом, в цилиндрических координатах положение произвольной точки пространства М определяется: расстоянием от её проекции 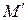 на плоскость хОу до начала координат; углом, на который нужно против часовой стрелки повернуть полярный луч
на плоскость хОу до начала координат; углом, на который нужно против часовой стрелки повернуть полярный луч 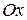 до совпадения с
до совпадения с 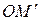 ; аппликатой
; аппликатой 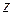 . Связь между декартовыми координатами точки
. Связь между декартовыми координатами точки 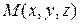 и цилиндрическими выражается формулами:
и цилиндрическими выражается формулами:
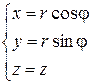 , , 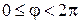 , , 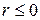 . .
| (64) |
Сферическая система координат
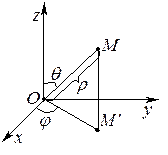 Идея полярной системы координат на плоскости нашла развитие и в сферической системе координат в пространстве. Положение точки М в сферической системе координат определяется тройкой чисел
Идея полярной системы координат на плоскости нашла развитие и в сферической системе координат в пространстве. Положение точки М в сферической системе координат определяется тройкой чисел 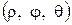 , где
, где 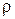 — расстояние от точки М до начала координат,
— расстояние от точки М до начала координат, 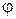 — угол отклонения против часовой стрелки луча Ох до совпадения с
— угол отклонения против часовой стрелки луча Ох до совпадения с 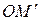 , а
, а 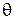 — угол между лучом Oz и радиус-вектором ОМ. Связь между декартовыми и сферическими координатами выражается формулами:
— угол между лучом Oz и радиус-вектором ОМ. Связь между декартовыми и сферическими координатами выражается формулами:
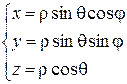 , ,  , , 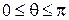 , , 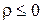 . .
| (65) |
Лекция 15
Поверхности второго порядка
Поверхности, задаваемые алгебраическими уравнениями второй степени относительно х, у, z, называют поверхностями второго порядка. Основными из них являются эллипсоид, одно- и двуполостный гиперболоиды, эллиптический и гиперболический параболоиды, цилиндрические и конические поверхности второго порядка. Канонические уравнения поверхностей второго порядка можно представить либо в виде
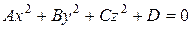 , ,
| (66) |
и тогда поверхности классифицируются следующим образом:
1) эллипсоид, если 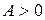 ,
, 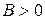 ,
, 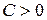 ,
, 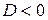 ;
;
2) однополостной гиперболоид, если 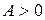 ,
, 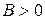 ,
, 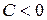 ,
, 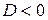 ;
;
3) двуполостной гиперболоид, если 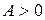 ,
, 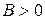 ,
, 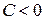 ,
, 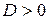 ;
;
4) эллиптический конус, если 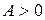 ,
, 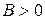 ,
, 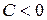 ,
, 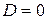 ;
;
5) эллиптический цилиндр, если 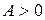 ,
, 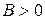 ,
, 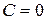 ,
, 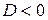 ;
;
6) гиперболический цилиндр, если 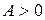 ,
, 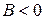 ,
, 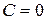 ,
, 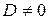 ;
;
либо в виде
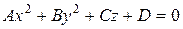 , ,
| (67) |
тогда поверхность является
1) эллиптическим параболоидом, если 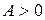 ,
, 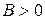 ,
, 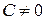 ;
;
2) гиперболическим параболоидом, если 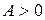 ,
, 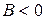 ,
, 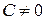 ;
;
3) параболическим цилиндром, если 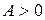 ,
, 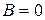 ,
, 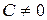 .
.
Рассмотрим канонические уравнения основных поверхностей без подробного описания принципов их построения. Заметим только, что для построения поверхностей часто рассматривают их сечения координатными плоскостями, а также плоскостями, параллельными координатным.
Поверхности второго порядка с центром симметрии
Эллипсоид задаётся уравнением
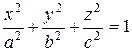 , ,
| (68) |
где а, b и c – полуоси.
Если 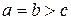 , то имеем сплющенный эллипсоид вращения, получающийся при вращении эллипса
, то имеем сплющенный эллипсоид вращения, получающийся при вращении эллипса 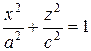 , лежащего в плоскости xOz вокруг его малой оси. При
, лежащего в плоскости xOz вокруг его малой оси. При  имеем вытянутый эллипсоид вращения
имеем вытянутый эллипсоид вращения 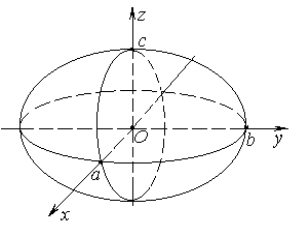 , который получается при вращении того же эллипса вокруг его большой оси. При
, который получается при вращении того же эллипса вокруг его большой оси. При  имеем сферу
имеем сферу 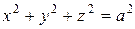 .
.
Сечением эллипсоида любой плоскостью является эллипс (в частном случае — окружность).
Определение 34. Прямолинейной образующей поверхности называется прямая линия, целиком лежащая на данной поверхности.
Определение 35. Направляющей поверхности называется кривая линия, при перемещении вдоль которой прямолинейной образующей формируется данная поверхность.
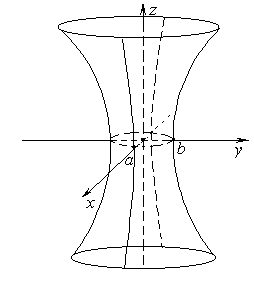
| Однополостной гиперболоид описывается уравнением
где а и b – действительные полуоси, а с – мнимая полуось. Однополостной гиперболоид имеет два семейства прямолинейных образующих: I. II.
|
где u и v — параметры, принимающие произвольные значения. Таким образом, через каждую точку поверхности проходят две прямые: по одной из образующих каждого семейства.
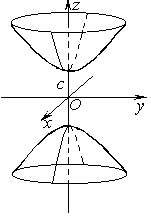
| Двуполостной гиперболоид задается уравнением:
где с – действительная полуось, а а и b – мнимые полуоси. Для обоих гиперболоидов сечения, параллельные оси Oz – гиперболы, а сечения, параллельные плоскости xOy – эллипсы. Если
| |||||
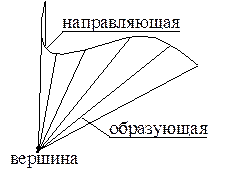
| Коническая поверхность образуется прямой линией — образующей, перемещающейся вдоль кривой линии — направляющей и имеющей неподвижную точку — вершину. |
Конус задаётся уравнением
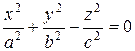 . .
| (71) |
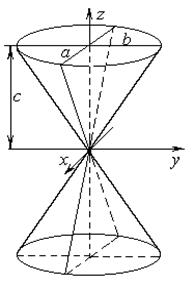 Он имеет вершину в начале координат; в качестве его направляющей кривой может быть взят эллипс с полуосями а и b, плоскость которого перпендикулярна оси Oz и находится на расстоянии с от начала координат. Этот конус является асимптотическим для обоих гиперболоидов
Он имеет вершину в начале координат; в качестве его направляющей кривой может быть взят эллипс с полуосями а и b, плоскость которого перпендикулярна оси Oz и находится на расстоянии с от начала координат. Этот конус является асимптотическим для обоих гиперболоидов 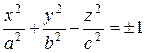 , то есть каждая из его образующих при удалении в бесконечность неограниченно приближается к обоим гиперболоидам. Если
, то есть каждая из его образующих при удалении в бесконечность неограниченно приближается к обоим гиперболоидам. Если 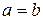 , то имеем прямой круговой конус.
, то имеем прямой круговой конус.
Поверхности второго порядка, не имеющие центра симметрии
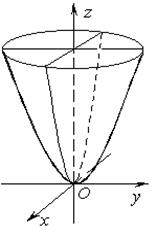 Эллиптический параболоид задаётся уравнением
Эллиптический параболоид задаётся уравнением
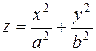 . .
| (72) |
Сечения, параллельные оси Oz – параболы; сечения, параллельные плоскости xOy – эллипсы. Если 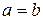 , то имеем параболоид вращения, получаемый при вращении параболы
, то имеем параболоид вращения, получаемый при вращении параболы 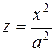 , лежащей в плоскости xOz, вокруг оси Oz.
, лежащей в плоскости xOz, вокруг оси Oz.
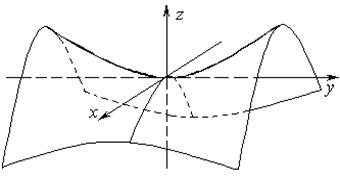 Гиперболический параболоид задаётся уравнением
Гиперболический параболоид задаётся уравнением
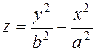 . .
| (73) |
Сечения, параллельные плоскости yOz — параболы; сечения, параллельные плоскости xOz — тоже параболы; сечения, параллельные плоскости xOy — гиперболы, а также пара пересекающихся прямых (при 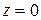 ).
).
Гиперболический параболоид подобно однополостному гиперболоиду имеет два семейства образующих:
I. 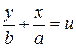 ,
, 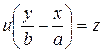 ; II.
; II. 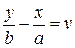 ,
, 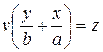 , где u и v — параметры. Через каждую точку поверхности тоже проходят две прямые: по одной из образующих каждого семейства.
, где u и v — параметры. Через каждую точку поверхности тоже проходят две прямые: по одной из образующих каждого семейства.
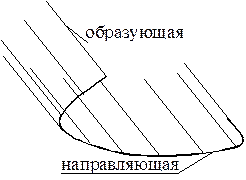 Цилиндрическая поверхность образуется прямой линией, перемещающейся параллельно заданному направлению вдоль некоторой кривой.
Цилиндрическая поверхность образуется прямой линией, перемещающейся параллельно заданному направлению вдоль некоторой кривой.
Форма цилиндра определяется его направляющей. Будем считать её расположеной в плоскости хОу, а образующие — параллельными оси Oz.
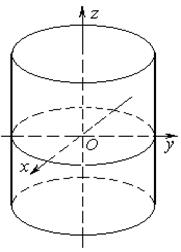 Различают три вида цилиндров:
Различают три вида цилиндров:
1) эллиптический цилиндр задаётся уравнением
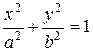 . .
| (74) |
Направляющей этого цилиндра служит эллипс с полуосями а и b, расположенный в плоскости хОу. Нетрудно видеть, что уравнение (54) направляющего эллипса в плоскости хОу в точности совпадает с уравнением (74), однако (54) рассматривается в  , а (74) — в
, а (74) — в  .
.
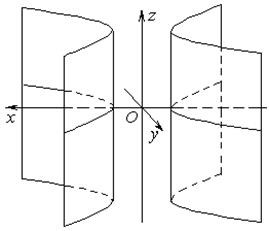
2) гиперболический цилиндр задаётся уравнением:
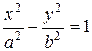 . .
| (75) |
Здесь направляющей линией в плоскости хОу является гипербола, уравнение которой (55) также в точности повторяет уравнение (75).
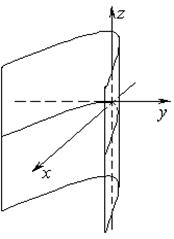
3) параболический цилиндр задаётся уравнением
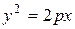 . .
| (76) |
Направляющей этого цилиндра является парабола в плоскости хОу, описываемая
Дата добавления: 2015-07-11; просмотров: 429 | Нарушение авторских прав