
Читайте также:
|
Решение задачи 1
Пусть, например  , тогда
, тогда 
 . Получили две точки А(3,0) и В(-3,0), принадлежащие данной кривой.
. Получили две точки А(3,0) и В(-3,0), принадлежащие данной кривой.
Решение задачи 2
Выделим полные квадраты при х и при у:


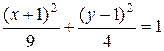 .
.
 Введем новую систему координат
Введем новую систему координат 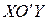 , полученную параллельным переносом старой системы на вектор
, полученную параллельным переносом старой системы на вектор  . При этом связь между координатами точек плоскости в старой и новой системах выражается формулами:
. При этом связь между координатами точек плоскости в старой и новой системах выражается формулами:  . Подставляя это в полученное уравнение, получаем каноническое уравнение
. Подставляя это в полученное уравнение, получаем каноническое уравнение  .
.
Решение задачи 3
Найдем точки пересечения этих линий, первая из которых является параболой, а вторая – прямой:

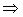

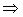

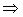
 ,
,  . Следовательно,
. Следовательно,  ,
,  . Получили точки пересечения
. Получили точки пересечения 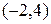 и
и  .
.
 При построении области сначала изображаются точки пересечения, прямая проводится через полученные точки, а для построения параболы нужно найти ещё её вершину, которая в данном случае совпадает с началом координат.
При построении области сначала изображаются точки пересечения, прямая проводится через полученные точки, а для построения параболы нужно найти ещё её вершину, которая в данном случае совпадает с началом координат.
Решение задачи 4
 Для получения полярного уравнения используем формулы (63):
Для получения полярного уравнения используем формулы (63):
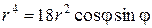

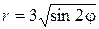 . Так как синус — периодическая функция, то можно построить таблицу значений на периоде, который для функции
. Так как синус — периодическая функция, то можно построить таблицу значений на периоде, который для функции  составляет интервал от 0 до
составляет интервал от 0 до  .
.
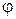
| 
| 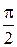
| 
| 
| |
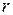
| - |
На промежутке между 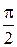 и
и  функция
функция  , то есть функция
, то есть функция 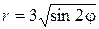 не определена на
не определена на  . Аналогичным образом функция ведёт себя на промежутках
. Аналогичным образом функция ведёт себя на промежутках  и
и  . Полученные точки соединим плавной кривой, которая носит название лемнискаты Бернулли.
. Полученные точки соединим плавной кривой, которая носит название лемнискаты Бернулли.
Решение задачи 5
 Сначала изобразим получившееся тело. Построим график параболы в плоскости хОу. Затем, вращая параболу вокруг оси Ох, получим пространственную фигуру — параболоид вращения (частный случай эллиптического параболоида). Ясно, что сечения этого параболоида плоскостями, перпендикулярными оси
Сначала изобразим получившееся тело. Построим график параболы в плоскости хОу. Затем, вращая параболу вокруг оси Ох, получим пространственную фигуру — параболоид вращения (частный случай эллиптического параболоида). Ясно, что сечения этого параболоида плоскостями, перпендикулярными оси 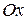 и проходящими через точку
и проходящими через точку  при
при  будут окружностями
будут окружностями  . Это и есть уравнение построенного параболоида вращения.
. Это и есть уравнение построенного параболоида вращения.
Точка 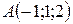 не удовлетворяет данному уравнению и, таким образом, не принадлежит данной поверхности. Примером точки, лежащей на заданной поверхности, может служить вершина параболлоида с координатами
не удовлетворяет данному уравнению и, таким образом, не принадлежит данной поверхности. Примером точки, лежащей на заданной поверхности, может служить вершина параболлоида с координатами  . Другая точка поверхности —
. Другая точка поверхности —  .
.
Решение задачи 6
Заданное уравнение определяет эллипсоид, сечение которого любой плоскостью является эллипсом. Пересекая данный эллипсоид плоскостью хОу, которая имеет уравнение  , получаем:
, получаем:

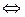

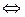
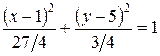 .
.
Итак, искомое сечение представляет собой эллипс в плоскости хОу с центром в точке  , с большой полуосью
, с большой полуосью  и малой полуосью
и малой полуосью  .
.
Решение задачи 7
Чтобы найти нужные точки пересечения, надо решить систему уравнений: 
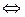

Имеем:

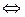

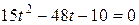

 ,
,  .
.
Система имеет два решения:  и
и  .
.
Дата добавления: 2015-07-11; просмотров: 58 | Нарушение авторских прав