
Читайте также:
|
| Название, каноническое уравнение, элементы | Чертеж | Линии уровня |
Эллипсоид
 ; ;  , ,  , ,  – полуоси; при – полуоси; при 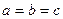 – сфера. – сфера.
| 
| При сечении плоскостью  ( ( ) – эллипсы ) – эллипсы 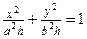 , ,  .
При сечении плоскостью .
При сечении плоскостью 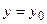 ( ( ) – эллипсы ) – эллипсы  , ,  .
При сечении плоскостью .
При сечении плоскостью  ( ( ) – эллипсы ) – эллипсы  , , 
|
Однополостный гиперболоид
 ; ;  , ,  – действительные полуоси, – действительные полуоси,  – мнимая полуось. – мнимая полуось.
| 
| При сечении плоскостью  – эллипсы – эллипсы 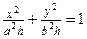 , ,  .
При сечении плоскостью .
При сечении плоскостью 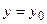 – гиперболы – гиперболы  , ,  .
При сечении плоскостью .
При сечении плоскостью  – гиперболы – гиперболы 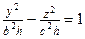 , , 
|
Двуполостный гиперболоид
 ; ;  , ,  – мнимые полуоси, – мнимые полуоси,  – действительная полуось. – действительная полуось.
| 
| При сечении плоскостью  ( (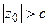 ) – эллипсы ) – эллипсы  , , 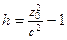 .
При сечении плоскостью .
При сечении плоскостью 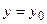 – гиперболы – гиперболы  , ,  .
При сечении плоскостью .
При сечении плоскостью  – гиперболы – гиперболы 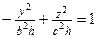 , , 
|
Конус
 ; ;  – вершина конуса. – вершина конуса.
| 
| При сечении плоскостью  ( (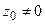 ) – эллипсы ) – эллипсы  , , 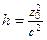 .
При сечении плоскостью .
При сечении плоскостью 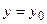 ( ( ) – гиперболы ) – гиперболы  , ,  .
При сечении плоскостью .
При сечении плоскостью  ( (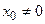 ) – гиперболы ) – гиперболы 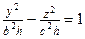 , ,  .
При сечении плоскостью .
При сечении плоскостью  – прямые – прямые  .
При сечении плоскостью .
При сечении плоскостью  – прямые – прямые 
|
| Название, каноническое уравнение, элементы | Чертеж | Линии уровня |
Эллиптический параболоид
 ; ;  – вершина эллиптического параболоида. – вершина эллиптического параболоида.
| 
| При сечении плоскостью  ( ( ) – эллипсы ) – эллипсы  , , 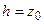 .
При сечении плоскостью .
При сечении плоскостью 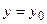 – параболы – параболы  , ,  .
При сечении плоскостью .
При сечении плоскостью  – параболы – параболы  , , 
|
Гиперболический параболоид
 ; ;  – вершина гиперболического параболоида. – вершина гиперболического параболоида.
| 
| При сечении плоскостью  ( ( ) – гиперболы ) – гиперболы  , , 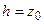 .
При сечении плоскостью .
При сечении плоскостью 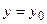 – параболы – параболы 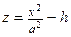 , ,  .
При сечении плоскостью .
При сечении плоскостью  – параболы – параболы 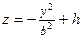 , ,  .
При сечении плоскостью .
При сечении плоскостью  – прямые – прямые 
|
Эллиптический цилиндр
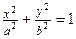
| 
| При сечении плоскостью  – эллипсы – эллипсы 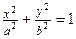
|
Гиперболический цилиндр

| 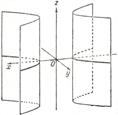
| При сечении плоскостью  – гиперболы – гиперболы 
|
Параболический цилиндр

| 
| При сечении плоскостью  – параболы – параболы 
|
Дата добавления: 2015-07-11; просмотров: 61 | Нарушение авторских прав