
|
Читайте также: |
Понятие и определение криволинейного интеграла по длине дуги и его вычисление
Понятие и определение криволинейного интеграла по координатам и его вычисление.
Теорема о независимости криволинейного интеграла от пути интегрирования.
Теорема Грина.
Формула вычисления площади плоской фигуры с помощью криволинейного интеграла.
Понятие и определение поверхностных интегралов 1 и 2 рода и их вычисление.
Поток вектора как поверхностный интеграл.
Теорема Остроградского и ее применение.
Вычисление площади поверхности, массы материальной поверхности, координат центра тяжести поверхности посредством поверхностных интегралов.
Теорема Стокса.
КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
Комплект 1
Задание 1. Вычислить криволинейный интеграл первого
рода от функции f (x, y) по длине дуги L
уравнениям y = 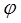 (х), a
(х), a  x
x  b
b
1.1 f (x, y)= x  ; L: y=ln x; 1
; L: y=ln x; 1  x
x  2
2
1.2 f (x, y) = y; L: y  = 2x от точки А(0;0)
= 2x от точки А(0;0)
до точки В(2; 2)
1. 3 f (x, y) =  ; L: отрезок прямой
; L: отрезок прямой
соединяющий точки
A (0;-2) и B (4;0)
1.4 f (x, y) = x + y; L: граница треугольника с
вершинами A(1;0), B(0;1)
1.5 f (x, y) =  ; L: -отрезок прямой
; L: -отрезок прямой
соединяющий точки
О (0;0) и A(1;2)
1.6 f (x, y) = x+2y; L: отрезок прямой от
точки A(1;1) до точки B(5;3)
1.7 f (x, y) =  ; L: y
; L: y  =
=  - от точки
- от точки
A(0;0) до точки B(1;0,6)
1.8 f (x, y) = 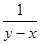 ; L: отрезок прямой
; L: отрезок прямой
соединяющий точки A(-1;0)
и B (2;0)
1.9 f (x, y) = 2x-y; L: отрезок прямой
соединяющий точки
A(2;2) и B(1;-3)
1.10 f (x, y) = 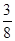 x
x  ; L: y =
; L: y = 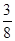 x
x  , 0
, 0  x
x  4
4
Дата добавления: 2015-07-11; просмотров: 89 | Нарушение авторских прав