Задание 1. Вычислить поверхностные интегралы

первого рода по

указанным поверхностям:

1.1 П: плоскость x + 2y +3z = 6, лежащая в октанте f(x,y,z) = 6x + 4y + 3z

1.2 П: y = , отсеченная плоскостями x = 0,

x = a; f(x,y, z) = x + 3y + z + 5

1.3 П: часть плоскости x + y + z =a, лежащая в октанте f(x,y,z) = 1

1.4 П: z = 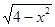,отсеченная плоскостями y = 0, y = 5 f(x,y,z) =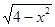

1.5 П: часть плоскости 6x + 4y + 3z = 12, лежащая в

октанте, f(x,y,z) = z + 2x +

1.6 П: z = 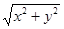, отсеченная плоскостью z =3;

f(x,y,z) = xyz

1.7 П: часть плоскости x + y + z =1, лежащая в

октанте, f(x,y,z) = 2x + y -

1.8 П: граница тела 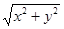z 1; f(x,y,z) =x + y

1.9 П: часть плоскости + + = 1, лежащая в октанте f(x,y,z) = x + y + z

1.10 П: часть плоскости 6x + 4y + 3z = 12, лежащая в

октанте f(x,y,z) = z + 2x +

Дата добавления: 2015-07-11