
Читайте также:
|
В настоящее время метод дисперсионного анализа, часть разработки основ которого принадлежит Р.Фишеру, многими исследователями признается одним из лучших методов определения коэффициента наследуемости в широком смысле. Сущность дисперсионного анализа состоит в изучении влияния одного или нескольких факторов на результативный признак. Применительно к рассматриваемой проблеме, результативный признак есть селекц-ионируемый признак, на степень количественного проявления которого влияют, как уже указывалось, две основных группы факторов: организованных (индивидуальные различия особей или клонов, входящих в состав популяции) и неорганизованных (слу-чайных, возникающих вследствие неоднородности среды обитания этих особей или клонов. Дисперсионный анализ позволяет четки разграничить степень влияния этих факторов на уровень обшей (фенотипической) изменчивости признака и популяции, при этом здесь используется известное в теории вероятностей свойство суммы центральных отклонений, согласно которому сумма частных дисперсий нескольких полностью независимых источников разнообразия признака всегда равна общей дисперсии, характеризующей общее разнообразие признака, возникшее под действием всех источников варьирования. В нашей частной задаче использования дисперсионного анализа это положение вариационной статистики нашло отражение в формулах (l) и (2).
Для изучения наследственной гетерогенности популяций применяются три основных способа. Основанных на методе диспер-сионного анализа:
1) наследуемость в широком смысле определяется по отношению факториальной суммы квадратов к общей сумме квадратов, т.е.
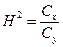 (11)
(11)
2) для определения коэффициента наследуемости вычисляются средние квадраты (вариансы) между классами (факториальная) и внутри классов (случайная варианса):

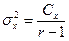 (12)
(12)
 (13)
(13)
где r – число классов, N – общее число наблюдений, из которых состоит дисперсионный комплекс. Средний квадрат внутри классов оценивает случайную дисперсию признака, возникающую под влиянием экологических условий, т.е. 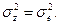 Для вычисления дисперсии, обусловленной наследственными различиями особей, применяют следующую формулу:
Для вычисления дисперсии, обусловленной наследственными различиями особей, применяют следующую формулу:
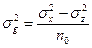 (14)
(14)
где n0 – при разном числе наблюдений среднее их число рассчитывают по формуле:
 (15)
(15)
где ri – число классов, ni – число наблюдений в каждом классе. При одинаковом числе наблюдений в классе n0 = ni, дальнейший расчет проводится по формуле (3);
3) для метамерных организмов с пространственно–топографической повторяемостью признаков, к которым относятся древесные растения, хорошим критерием наследственной обусловленности признака служит коэффициент повторяемости:

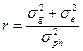 (16)
(16)
где  – генотипическая компонента обшей фенотипической вариансы,
– генотипическая компонента обшей фенотипической вариансы,
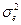 – межиндивидуальная средовая компонента, обусловленная специфическими для каждой особи внешними или внутренними наследственными факторами. Из формулы (16) видно, что коэффициент повторяемости является верхним пределом коэффициента наследуемости в широком смысле, т.е. при
– межиндивидуальная средовая компонента, обусловленная специфическими для каждой особи внешними или внутренними наследственными факторами. Из формулы (16) видно, что коэффициент повторяемости является верхним пределом коэффициента наследуемости в широком смысле, т.е. при 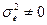 , r>H2, а при
, r>H2, а при 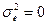 r=H2.
r=H2.
Пример. Определить наследуемость количественного содержания хлорофилла в листьях в экспериментальной популяции, состоящей из следующих пяти клонов (табл.5).
Порядок выполнения расчетов сводится к следующему:
1. Общая средняя
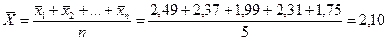
2. Сумма квадратов отклонений от общей среднеймеждуклонами
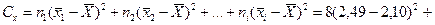

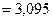
3. Сумма квадратов отклонений от средних внутри клонов (т.е. между отдельными растениями клона и среднимзначениемпризнака в клоне) 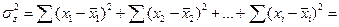
= 1,4696 + 0,2835 + 0,1906 + 0,9014 + 0,1905 = 3,035
4. Средний квадрат между клонами
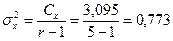
5. Средний квадрат внутри клонов
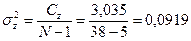
6. Критерий Фишера 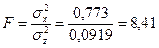
7. Стандартный критерий 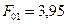
8. Экологическая варианса признака 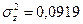
9. Среднее число наблюдений в клоне:
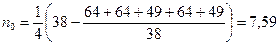
10. Генотипическая варианса:

11. Наследуемость признака по формуле (11):
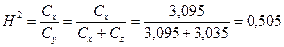
12. Наследуемость признака по формуле (3):
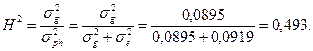
Как видно, значения коэффициентов наследуемостипризнака,определенные двумя различными способами, практически совпали. Первый способ значительно более прост в употребление, однако в последнее время он подвергается критике вследствие недостаточного его теоретического обоснования, хотя он имеетодновременно много сторонников его использования. Прирасчетекоэффициента наследуемости по второму способу (с разложением средних квадратов) нужно принять во внимание тообстоятельство, что определение наследуемости будет иметьсмысллишь при условии F> Fst.
Таблица 5. Изменчивость содержания хлорофилла (а+b) в листьях различных клонов тополей (мг/г сырого веса)
| Клон № 1 | ||

| 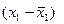
| 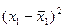
|
| 3,19 | +0,70 | 0,4900 |
| 2,45 | -0,04 | 0,0016 |
| 1,96 | -0,53 | 0,2809 |
| 2,20 | -0,29 | 0,0841 |
| 2,38 | -0,11 | 0,0121 |
| 2,45 | -0,04 | 0,0016 |
| 2,12 | -0,37 | 0,1369 |
| 3,17 | +0,68 | 0,4624 |

| – | 1,4696 |
| Клон № 2 | ||
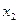
| 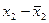
| (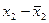 )2 )2
|
| 2,54 | +0,17 | 0,0289 |
| 2,20 | -0,17 | 0,0289 |
| 2,47 | +0,10 | 0,0100 |
| 2,32 | -0,05 | 0,0025 |
| 2,58 | +0,21 | 0,0441 |
| 2,62 | +0,25 | 0,0625 |
| 2,12 | -0,25 | 0,0625 |
| 2,16 | -0,21 | 0,0441 |
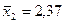
| – | 0,2835 |
| Клон №3 | ||
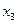
| 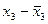
| 
|
| 2,05 | +0,06 | 0,0036 |
| 2,01 | +0,02 | 0,0004 |
| 1,98 | -0,01 | 0,0001 |
| 2,01 | +0,02 | 0,0004 |
| 2,32 | +0,33 | 0,1089 |
| 1,75 | -0,24 | 0,0576 |
| 1,85 | -0,14 | 0,0196 |
| – | – | – |
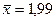
| – | 0,1906 |
| Клон № 4 | ||
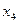
| 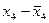
| 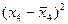
|
| 1,85 | -0,46 | 0,2116 |
| 1,86 | -0,45 | 0,2025 |
| 2,77 | +0,46 | 0,2116 |
| 2,08 | -0,23 | 0,0529 |
| 2,31 | ||
| 2,57 | +0,26 | 0,0676 |
| 2,67 | +0,36 | 0,1296 |
| 2,47 | +0,16 | 0,0256 |
| – | 0,9014 |
| Клон № 5 | ||
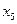
| 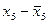
| 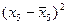
|
| 1,58 | -0,19 | 0,0361 |
| 1,66 | -0,09 | 0,0081 |
| 2,04 | +0,29 | 0,0841 |
| 1,76 | +0,01 | 0,0001 |
| 1,54 | -0,21 | 0,0441 |
| 1,81 | +0,06 | 0,0036 |
| 1,87 | +0,12 | 0,0144 |
| – | – | – |
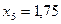
| – | 0,1905 |
Дата добавления: 2015-07-11; просмотров: 60 | Нарушение авторских прав