Образец задания. Пример. В прямоугольном ▲ ABC известны длина гипотенузы: AB равная числу 12,5

Пример. В прямоугольном ▲ ABC известны длина гипотенузы: AB равная числу 12,5, и косинус угла ABC, равный числу 44/125. Найти величины синуса угла CAB и площадь треугольника. Дано: с = 12,5 и cos В = 44/125. Найти sin А и S.

Решение: имеем sin а = а/с = cos В = 44/125 = 0,325;

Ответ: 0,325; 25,74.

Пример. В условиях предыдущей задачи найти периметр треугольника и радиус вписанной в него окружности. Решение: имеем b = с * sinВ = 12,5 * 0,936 = 11,7; 2р = а + b + с = 4,4 + 11,7 + 12,5 = 28,6; p= 14,3; S = р * г; r=S/p = 22,74/14,3 =1,8.

Ответ: 28,6; 1,8.

Пример. В треугольнике даны длины трех сторон, равные 41, 84, 85. Вычислить радиус вписанной и удвоенный радиус описан­ной окружностей.

Дано: а = 41, b = 84, с = 85. Найти г и R.

Решение: радиусы г и R легко выражаются через площадь S треугольника. Кроме того, площадь можно найти по формуле Герона:

имеем р(а + b + с)/2 = (41 + 84 + 85)/2 =105; тогда

r = S/p =1680/105 = 16, 2R = a*b*c/2S = 41*84*85/2* 1680 = 87,125.

Ответ: 16; 87,125.

Задание 5. Набрать текст и формулы по образцу.

Образец задания

Точки Х₁ = -1, Х₂ = 5/4, Х₃ = 2 делят числовую ось на четыре про­межутка.

Найдем знаки произведения на каждом интервале и отметим их на схеме. Решением неравенства (АХ- 5)(Х- 2)(Х+ 1) > 0 является объединение двух промежутков [-1; 5/4] и [2; ©о].

Решением неравенства является объединение промежутков [-1; 5/4] и [2; 3]. Серединами этих промежутков являются числа 0,125 и 2,5.

Ответ: 0,125; 2,5.

Пример.

(2Х+ 1): (X²- Y²+ 1) > 2/(Х-2),

где 7=(-Х)¹/².

Решение: Область допустимых значений (ОДЗ)

При ХєЕ неравенство примет вид

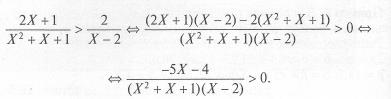
Квадратный трехчлен Х²+ Х+ 1 положителен при всех X, так как его дискриминант отрицателен и коэффициент при (Х²+ Х+ 1) > 0, получим равносильное неравенство.

Дата добавления: 2015-07-11