Основные теоретические положения. Матричные (балансовые) модели представляют собой математическое выражение

Матричные (балансовые) модели представляют собой математическое выражение балансового метода планирования (метод взаимного сопоставления затрат и результатов).

Матричные модели включают в себя общий принцип построения задач, единство системы расчетов и аналогичность ряда экономических характеристик.

В качестве примера указанных моделей рассмотрим статические динамические модели межотраслевого стоимостного баланса, межпродуктовый баланс для обеспечения взаимоувязки планов производства группы предприятий или обособленных подразделений (цехов или иных структур) одной организации.

Межотраслевой баланс отражает производство и распределение валового национального продукта по отраслям, межотраслевые потоки, использование материальных и трудовых ресурсов, создание и распределение национального дохода.

Экономико-математические методы (ЭММ) межотраслевого баланса представляет собой систему уравнений, отражающих функциональную взаимосвязь включенных в его систему элементов:

где - вектор валовой продукции,

- вектор конечной продукции (конечное потребление и накопление).

– производственные (материальные)затраты -й отрасли продукции -й отрасли в течении планового периода (например, если отрасль 1– угольная, отрасль 2 – черная металлургия, то – годовые затраты угля на производство черных металлов).

С учетом того, что = система уравнений перепишется в виде:

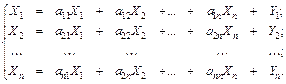
или в более компактном виде:

,

(запись с использованием знаков суммирования):

,

(запись в матричной форме).

Именно, в этих двух формах записи и используется ЭММ межотраслевого баланса, которую называют моделью Леонтьева или моделью «затраты – выпуск».

Элементы 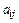матрицы А называют коэффициентами прямых (материальных) затрат или технологическими коэффициентами – это затраты -й отрасли на единицу (рубль) валовой продукции -й отрасли.

Матрицу 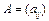, где , называют матрицей прямых материальных затрат.

Технологические коэффициенты имеют следующие свойства:

1)

2) ; , т.е. сумма элементов матрицы A по любому из столбцов меньше 1.

В матричной форме модель Леонтьева можно записать в виде:

или .

Последнее соотношение можно использовать для анализа и планирования решения следующих задач:

§ определение объемов конечного продукта отраслей по заданным объемам валовой продукции:

;

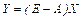§ определение валовой продукции отраслей по заданным объемам конечной продукции:

.

Элементы - обратной матрицы называют коэффициентами полных (материальных) затрат – это затраты

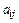-й отрасли на каждый рубль конечной продукции , т.е. коэффициент показывает каков должен быть валовой выпуск -й отрасли для того, чтобы обеспечить выпуск единицы конечного продукта -й отрасли; он не меньше коэффициента прямых материальных затрат , и .

Соответственно матрицу В называют матрицей коэффициентов полных затрат, а матрицу А – матрицей коэффициентов прямых затрат.

Неотрицательную матрицу 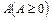называют продуктивной, если существует хотя бы один такой положительный вектор Х > 0,

что (Е - А)Х > 0.

Это определение имеет простой экономический смысл: матрица А продуктивна, если существует такой план Х, что каждый объект (отрасль, предприятие, цех) может произвести некоторое количество конечной продукции.

Продуктивность матрицы является необходимым и достаточным условием существования, единственности и неотрицательности решения системы уравнений 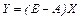при любом неотрицательном векторе .

Поэтому для определения продуктивности матрицы А надо чтобы выполнялись условия:

— существовала обратная матрица .

— максимальное собственное число матрицы А было меньше единицы, т.е. (собственными числами квадратной матрицы А называются корни характеристического уравнения ).

Рассмотрим межпродуктовую балансовую модель на примере предприятия, у которого в каждом цехе производиться один вид продукции в объёме . Отдельный вид продукции может быть использован как промежуточный продукт, идущий на внутреннее потребление (передаваемый другим цехам), и как конечный продукт, поступающий непосредственно потребителю.

Обозначим через - количество продукции – -го вида, потребляемой для изготовления j -й продукции в количестве 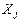, через – выпуск конечной продукции -го вида.

Общий (валовый) выпуск продукции i -го вида (потребность в ее производстве) равен сумме промежуточного и конечного продукта:

.

Обозначим через норму расхода продукции i -го вида на производство продукции j -го вида, т. е. – это коэффициент прямых затрат, значит . Тогда 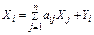. Система балансовых уравнений в матричной форме имеет вид .

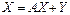Используя это матричное уравнение, можно найти:

§ валовой выпуск продукции Х;

§ распределение продукции между цехами путем умножения коэффициентов прямых затрат на общий выпуск:

.

Задачи

2.1. Оценить продуктивность матрицы:

.

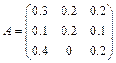Дата добавления: 2015-07-11