Дифракция волн.

В упрощенном смысле под дифракцией понимают круг явлений, в которых проявляется отступление от прямолинейного распространения волн. Такое понимание дифракции, вообще говоря, неверно, поскольку прямолинейное распространение волн является лишь определенным приближением. Действительно, специфика любого волнового движения проявляется в том, что это движение, возникнув вначале в ограниченной области, стремится распространиться в равной степени во все стороны. Выбором специальной формы этой области можно добиться того, что волна побежит преимущественно в некоторых направлениях. Вдоль одного из таких направлений побежит фрагмент волны, который с определенной точностью можно считать движущимся прямолинейно.

Для наблюдения основных закономерностей дифракции видоизменим характер возбуждения волн на поверхности воды в описанном ранее опыте. В качестве источника волны вместо шариков будем использовать пластину O₁O₂, длина которой 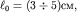т.е. заметно превышает длину волны 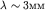(рис. 5.22). В результате по поверхности воды побежит "плоская" волна в направлении, перпендикулярном пластине. Отчетливо наблюдаются две прямолинейные границы Г₁ и Г₂, отделяющие возмущенную волной и гладкую части поверхности воды. Для этой последней части можно употребить заимствованный из оптики термин: "область геометрической тени". Саму волну часто называют волновым пучком, или лучом. В этом эксперименте можно считать, что волна распространяется прямолинейно и не заходит в область тени. Это связано с тем, что размер ее волнового фронта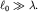

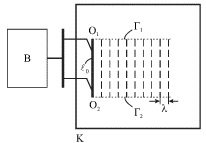Рис. 5.22.

Уменьшим теперь этот размер. Это наиболее просто осуществить, если параллельно пластине O₁O₂ установить две вертикальные стенки С₁ и С₂, расстояние между которыми можно изменять (рис. 5.23).

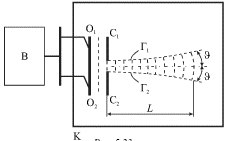Рис. 5.23.

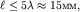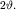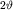Если сделать то волна начнет постепенно заходить в область тени, а ее фронт будет искривляться. На некотором характерном расстоянии волновой пучок приобретет заметную угловую расходимость и далее будет распространяться по части поверхности, ограниченной углом При уменьшении зазора между стенками угол возрастает, а расстояние уменьшается. Это отступление от прямолинейного распространения является результатом дифракции, существенно тогда, когда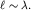

Не составляет труда оценить величины и 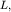используя подход, предложенный французским ученым О. Френелем в XIX столетии для объяснения дифракции световых волн. Следуя Френелю, участок фронта падающей волны в зазоре между стенками можно рассматривать как цепочку из 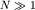близко расположенных одинаковых точечных источников 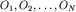(рис. 5.24).

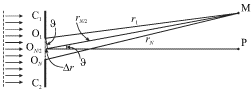Рис. 5.24.

Возмущение в любой точке M поверхности воды есть результат интерференции 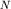волн от этих, так называемых "вторичных" источников, и зависит от разности хода всех интерферирующих волн. В практически важных случаях расстояния 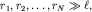поэтому отрезки 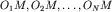можно считать параллельными. Понятно, что в точку P, лежащую на оси волнового пучка, интерферирующие волны приходят в фазе и возмущение поверхности в ней будет максимальным. Напротив, в точке M волны могут погасить друг друга, если разность хода 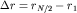между волнами от крайнего источника O₁ и среднего источника 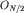будет равна 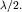Поскольку эта разность, как видно из рис. 5.24, равна 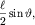то

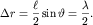(5.51)

Аналогично, в противофазе будут приходить волны и от других пар источников 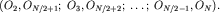Говорят, что в точке M будет наблюдаться первый минимум дифракционной картины. Не составляет труда написать условие, подобное (5.51), и для других минимумов. Однако, как показывает строгий анализ, более 90% всей энергии переносится волной в пределах угла 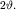Поэтому на рисунке (5.23) границы Г₁ и Г₂ весьма условны и очерчивают лишь основную, наиболее энергоемкую часть пучка.

Для оценки дифракционной расходимости волновых пучков используется угол 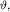который при 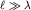оценивается согласно (5.51) по формуле

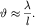(5.52)

Такую расходимость пучок приобретает на некотором характерном расстоянии 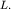Его можно легко оценить из рисунка 5.25, на котором пунктиром изображены асимптоты к границам Г₁ и Г₂. Будем условно считать, что на расстоянии поперечный размер пучка удвоился и стал равным 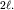Тогда с учетом (5.52) мы можем записать:

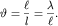(5.53)

Отсюда

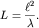(5.54)

Величина называется дифракционной длиной пучка с длиной волны и поперечным размером Она определяет масштаб расстояний, на которых развивается заметная дифракция пучка.

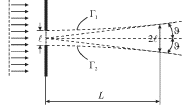
Рис. 5.25.

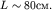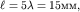Сделаем некоторые оценки. В опыте, изображенном на рисунке (5.22), и Это означает, что в кювете дифракция просто не успевает заметно развиться. При уменьшении (рис. 5.23) до величины дифракционная длина пучка 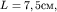и дифракция становится отчетливо видна.

Если на пути волнового пучка поставить препятствие - стенку С (рис. 5.26), то сразу за стенкой будет тень, однако волна, пройдя расстояние 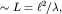обогнет препятствие. Иллюстрацией к сказанному является, например, возможность услышать звуковой сигнал автомобиля, находясь позади небольшого строения. Однако за многоэтажный дом звук практически не проникает.

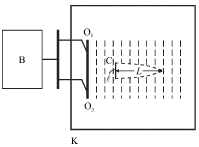
Рис. 5.26.

Волны на поверхности жидкости. Гравитационные волны. Капиллярные волны. Цунами. Внутренние волны. Акустические волны большой амплитуды. Линейный и нелинейный режимы распространения. Уединенные волны (солитоны).

Дата добавления: 2015-07-11