Гипотеза Де Бройля. Дифракция электронов

В предшествующих главах было показано, что свет в зависимости от условий его изучения проявляет как волновые, так и корпускулярные свойства. Иногда в этом усматривают «противоречивость» свойств света, говорят о «корпускулярно-волновом дуализме». Однако правильнее относить эту «противоречивость» не к природе, а к нашим представлениям о ней, недостаточно приспособленным для описания сложных физических явлений.

В 1923—1924 гг. Луи де Бройль пришел к заключению, что если свет обладает и волновыми, и корпускулярными свойствами (фотоны), то и частицы вещества также могут обладать, кроме корпускулярных, и волновыми свойствами, о чем физики того времени не задумывались. Как известно, фотон характеризуется импульсом

и энергией

E=hv=pc

Де Бройль по аналогии предположил, что любой частице вещества массой т, движущейся со скоростью и, также можно сопоставить волновой процесс, причем длина волны должна равняться:

(12.1)

Так как кинетическая энергия частицы равна:

то длину волны можно выразить и через кинетическую энергию:

Кроме того, если полная энергия частицы в соответствии со специальной теорией относительности есть Е=тc², то частице следует сопоставить и частоту

а также волновое число

Найдем теперь фазовую скорость волны де Бройля:

Так как ν_ф связана с групповой скоростью волны соотношением:

то оказывается, что групповая скорость волны де Бройля равна скорости самой частицы:

u=v.

Таким образом, волны де Бройля. Испытывают дисперсию даже в вакууме. Природу введенного им волнового процесса де Бройль не обсуждал. Во всяком случае, волны де Бройля не электромагнитные, так как они присущи и частицам, лишенным заряда либо движущимся с постоянной скоростью равномерно и прямолинейно, т.е. частицам, не дающим электромагнитного излучения. Дисперсия в вакууме также существует для волн электромагнитной природы. В параграфе 14.7 будут освещены еще некоторые свойства волн де Бройля.

Опытное подтверждение гипотезы де Бройля о существовании волновых свойств частиц вещества было получено в опытах Девиссона и Джермера, изучавших отражение электронов от поверхности кристаллов. В этих опытах было установлено два замечательных факта:

1) При изменении угла падения электронов данной скорости отражение имеет резко выраженный максимум при углах падения, удовлетворяющих условию Вульфа-Брэгга, полученному ранее для отражения рентгеновских лучей от кристаллов:

(здесь d- расстояние между атомными плоскостями кристалла, параллельными его поверхности, α – угол скольжения падающего пучка, λ — длина волны Де Бройля).

2) Еще более поразительным оказался второй результат. При данном угле падения и изменении скорости электронов v, что достигалось изменением анодного спряжения U, ускоряющего электроны, интенсивность отражение пучка периодически изменялась (рис. 12.1, кривая 1), причем эта закономерность напоминала закономерность, наблюдаемую при отражении рентгеновских волн различной длины от некоторого кристалла при неизменном угле падения (рис. 12.1, кривая 2).

Рис 12.1

Так как энергия электрона, приобретенная при прохождении разности потенциалов U, равна:

то абсциссы кривой 1 пропорциональны длинам волн де Бройля.

Оценка длин волн дает:

(12.2)

при (U=400 В, что отвечает условиям опыта, это дает

λ=6,2 x 10^-11 м.

Позже Дж. Томсон, П. С. Тартаковский и другие физики получили дифракционные кольца, пропуская электроны через тонкие слои металла (аналогия с опытами Дебая-Шерера в области рентгеновских лучей, см. § 4.5).

Электронная дифракционная картина очень похожа на рентгеновскую дебаеграмму. Чтобы доказать, что она не вызвана вторичными рентгеновскими лучами, возникающими при торможении электронов в веществе, вдоль фотопластинки, где образовывалась электронная дебаеграмма, создавалось магнитное поле. При этом вся картина смещалась поперек поля. Если бы картина создавалась рентгеновскими, лучами, то никакого смещения не получалось бы.

Позже дифракцию наблюдали и для более тяжелых заряженных частиц — протонов, ионов гелия и др., а также и для нейтральных атомов, причем соотношение (12.1) хорошо подтвердилось.

Так как длина волны де Бройля обратно пропорциональна' массе частицы, то у макроскопических тел волновые свойства практически не проявляются. Действительно, пылинка массой 10^-6 кг, движущаяся со скоростью 10 м/с, характеризуется очень малой длиной волны де Бройля (λ = 6,6-10^-29 м), не проявляющейся в современных экспериментах.

4 вопрос

Волновая функция и ее статический смысл.

Чтобы устранить эти трудности, не­мецкий физик М. Борн (1882-1970) в 1926 г. предположил, что по волно­вому закону меняется не сама вероят­ность, а некая величина, названная ам­плитудой вероятности, обозначаемая . Эту величину называют также волновой функцией (или 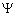-фун­кцией). Амплитуда вероятности может быть комплексной, и вероятность W про­порциональна квадрату ее модуля:

(6.1)

Таким образом, описание состояния мик­рообъекта с помощью волновой функции имеет статистический, вероятностный характер: квадрат модуля волновой функ­ции (квадрат модуля амплитуды волн де Бройля) определяет вероятность на­хождения частицы в момент времени t в об­ласти с координатами х и х + dx, у и у + dy.: и z + dz.

Итак, в квантовой механике состояние микрочастиц описывается принципиально по-новому — с помощью волновой функ­ции, которая является основным носителем информации об их корпускулярных и вол­новых свойствах. Вероятность нахожде­ния частицы в элементе объема dV равна

, (6.2)

где величина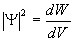

(квадрат модуля Т-функции) имеет смысл плотности вероятности. Таким образом, физический смысл имеет не сама 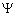-функция, а квадрат ее модуля 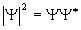( -функция, комплексно-сопряженная с 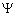), которым определяется интенсив­ность волн де Бройля.

Вероятность найти частицу в момент времени t в конечном объеме V, согласно теореме сложения вероятностей, равна

.

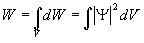Поскольку 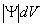определяется как ве­роятность, необходимо волновую функцию Т нормировать так, чтобы ве­роятность W достоверного события об­ращалась в единицу, если за объем V принять бесконечный объем всего про­странства. Это означает, что при данном условии частица должна находиться где-то в пространстве. Следовательно, условие нормировки вероятностей

(6.3)

где тройной интеграл (6.3) вычисляет­ся по всему бесконечному пространству, т. е. по координатам х, у. z от до . Таким образом, условие (6.3) говорит об объективном существовании частицы во времени и пространстве.

Чтобы волновая функция являлась объ­ективной характеристикой состояния ми­крочастиц, она должна удовлетворять ряду ограничительных условий. Функция Т, характеризуя вероятность обнаружения действия микрочастицы в элементе объ­ема, должна быть конечной (вероятность не может быть больше единицы), од­нозначной (вероятность не может быть не однозначной величиной) и непрерывной (вероятность не может изменяться скач­ком).

Волновая функция удовлетворяет прин­ципу суперпозиции: если система может находиться в различных состояниях, опи­сываемых волновыми функциями то она также может нахо­диться в состоянии 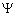, описываемом ли­нейной комбинацией этих функций:

где Сn (n = 1,2,…) — некоторые комплекс­ные числа. Сложение волновых функций (амплитуд вероятностей), а не вероят­ностей (квадратов волновых функций) принципиально отличает квантовую тео­рию от классической статистической тео­рии, в которой для независимых собы­тий справедлива теорема сложения веро­ятностей.

Зная волновую функцию 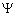в квантовой механике, вычисляют средние значения физических величин, характеризующих данный микрообъект. Например, среднее расстояние <r> электрона от ядра вы­числяют по формуле:

где интегрирование производится, как и в случае (6.3).

Уравнение Шредингера

Статистическое толкование волн де Бройля и соотношение неопределенностей Гейзенберга привели к выводу, что уравнением дви­жения в квантовой механике, описывающим движение микрочастиц в различ­ных силовых полях, должно быть урав­нение, из которого бы вытекали наблю­даемые на опыте волновые свойства ча­стиц. Основное уравнение должно быть уравнением относительно волновой фун­кции 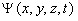, так как именно она, или, точнее, величина , определяет вероятность пребывания частицы в момент времени t в объеме , т. е. в области с координатами х и x+dx, у и у+dy, z и z + dz. Так как искомое уравнение должно учитывать волновые свойства частиц, то оно должно быть волновым уравнением, подобно уравне­нию, описывающему электромагнитные волны.

Основное уравнение нерелятивистской квантовой механики сформулировано Э. Шредингером (1926). Уравнение Шре­дингера, как и все основные уравнения физики (например, уравнение Ньютона в классической механике и уравнения Максвелла для электромагнитного поля), не выводится, а постулируется. Правиль­ность этого уравнения подтверждается согласием с опытом получаемых с его по­мощью результатов, что, в свою очередь, придает ему характер закона природы. Уравнение Шредингера имеет вид

(7.1)

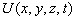где , m – масса частицы, – оператор Лапласа , i – мнимая единица, - потенциальная энергия частицы в си­ловом поле, в котором частица движется.

5 вопрос

Корпускулярно-волновой дуализм – свойство любой микрочастицы обнаруживать признаки частицы (корпускулы) и волны. Наиболее ярко корпускулярно-волновой дуализм проявляется у элементарных частиц. Электрон, нейтрон, фотон в одних условиях ведут себя как хорошо локализованные в пространстве материальные объекты (частицы), двигающиеся с определёнными энергиями и импульсами по классическим траекториям, а в других – как волны, что проявляется в их способности к интерференции и дифракции. Так электромагнитная волна, рассеиваясь на свободных электронах, ведёт себя как поток отдельных частиц – фотонов, являющихся квантами электромагнитного поля (Комптона эффект), причём импульс фотона даётся формулой р = h/λ, где λ – длина электромагнитной волны, а h – постоянная Планка. Эта формула сама по себе – свидетельство дуализма. В ней слева – импульс отдельной частицы (фотона), а справа – длина волны фотона.
Дуализм электронов, которые мы привыкли считать частицами, проявляется в том, что при отражении от поверхности монокристалла наблюдается дифракционная картина, что является проявлением волновых свойств электронов. Количественная связь между корпускулярными и волновыми характеристиками электрона та же, что и для фотона: р = h/λ (р – импульс электрона, а λ – его длина волны де Бройля).
Корпускулярно-волновой дуализм лежит в основе квантовой физики.

6 вопрос

Дата добавления: 2015-07-12