Волны в жидкостях и газах.

В жидкостях и газах возможны лишь деформации сжатия и растяжения, поэтому в них могут распространятся только продольные волны. Хотя мы ранее и рассчитывали скорость распространения возмущений в газе, тем не менее вычислим скорость распространения продольных волн с использованием волнового уравнения. 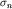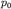Последнее может быть получено из (4.74), в котором следует заменить величиной где - давление в волне, - равновесное давление в среде, - возмущение давления. Тогда мы можем записать

(5.5)

Чтобы из (5.5) получить волновое уравнение, необходимо знать материальное уравнение среды

(5.6)

Качественно эта зависимость изображена на рис. 5.6. При очень малых возмущениях плотности и давления из (5.6) получаем:

(5.7)

где введено обозначение

(5.8)

Рис. 5.6.

С учетом (4.69) и (4.72) возмущения плотности в (5.7) связаны со смещением s соотношением:

(5.9)

Следовательно, (5.7) примет вид:

(5.10)

Подставляя (5.10) в (5.5), записывая и переходя к пределу при получим волновое уравнение

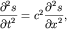(5.11)

из которого сразу видно, что скорость волны задается выражением (5.8) и не зависит от частоты (дисперсия отсутствует). Естественно, что с такой скоростью распространяются волны с длиной волны 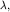превосходящей длину свободного пробега молекул в газе или межатомные расстояния в жидкостях В этом случае жидкость и газ могут рассматриваться как сплошные среды. Для волн высоких частот, когда 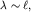возникает дисперсия, а волны с длиной 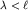распространяться вообще не могут.

Упругие волны в жидкостях и газах, как, впрочем, и в твердых телах, называются акустическими, а раздел физики, который их изучает - акустикой. Частоты этих волн лежат в диапазоне от долей герца (инфразвук) до 10¹³ Гц (гиперзвук). Этим частотам соответствуют длины волн от десятков километров до нескольких ангстрем. Значения скоростей (фазовых и групповых) для разных сред лежат в диапазоне от долей до десятков км/с.

Для воздуха материальное уравнение (5.6) является уравнением адиабаты и в акустике обычно записывается в виде (см. также предыдущие лекции):

(5.12)

где - показатель адиабаты.

Тогда из (5.8) скорость волны (в акустике употребляют термин "скорость звука") в газе получается равной

(5.13)

где – молярная масса газа.

Скорость звука зависит, таким образом, от рода газа и по порядку величины совпадает со средней скоростью теплового движения молекул.

Для жидкости материальным уравнением является полуэмпирическое уравнение Тета:

(5.14)

где – характерное внутреннее давление, обусловленное межмолекулярным взаимодействием (оно составляет для большинства жидкостей без пузырьков и различных включений несколько тысяч атмосфер). Параметр имеет порядок нескольких единиц (например, для воды ).

В таблице приведены значения скорости звука, измеренные в некоторых газах (при температуре ) и жидкостях.

Дата добавления: 2015-07-11