
|
Читайте также: |
© А.Ф. Черняев, 2004.
Преамбула
Настоящая работа, посвященная диалектическому обоснованию нового математического направления - «физической геометрии», является попыткой объединения нескольких геометрических идей, высказанных автором в последнем десятилетии ХХ века. Идеи эти, хотя и базировались на законах диалектики, и относились к одному разделу математики, были разрозненными, отрывочными, и потому довольно сложными для понимания. Диалектическое обоснование их проводилось недостаточно убедительно, да и отношение математиков (как и физиков) к диалектике, оставляет желать лучшего.
Математики,похоже, уверены в том, что законы диалектики неприменимы к математике, поскольку математика наука абстрактная и количественная, имеющая дело с обезличенными числами, а диалектика основывается на качественных категориях. Математика оказывается единственной наукой, в которой категория «качество» практически отсутствует. Считается, что все математические операции (включая движение) есть числовые бескачественные преобразования, не изменяющие качества чисел и безотносительные к ним. Сама же математика - формальная наука о количественном изменении числовых величин, не содержащих в себе никакого качества. А потому диалектика не вхожа в апартаменты, в которых властвует математика. Получается так, что для философов математика чужой монастырь. Не случайно диалектики в течение тысячелетий стараются обходить стороной его укрепления, разражаясь, время от времени, тирадами гносеологических залпов, стремящихся доказать «подчиненность» математики законам диалектики. Эта боязнь математического формализма и обусловила математике особый статус абстрактной, не зависимой от философии науки. Даже Гегель, понимая математику как науку о количественных величинах и числах, не заметил в количественных закономерностях математики внутренней диалектики ее качественных основ и надолго «законопатил» философам вход в храм математики, охарактеризовав бесконечную последовательность натурального числового ряда «дурной бесконечностью».
И эта бесконечность будет оставаться «дурной» до тех пор, пока мы не увидим за каждым математическим числом, понятием или аксиомой их качественную составляющую. То есть то, что и является основой диалектического анализа, то, без чего любая наука, включая математику, остается гносеологически запутанной, внесистемной и поверхностной регистрацией отдельных количественных или качественных проявлений, не сводимых к одной системе взаимосвязанных знаний.
Особенность русской (динамической) геометрии и заключается в том, что она, на наш взгляд, первая из математических наук, основывающаяся на диалектических законах и развивающаяся не как абстрактная дисциплина, а как дисциплина, полностью базирующаяся на практике. Более того, у нее отсутствуют даже предпосылки возможного «отдаления» от практики, поскольку она опирается на динамику реальных физических процессов.
Однако история показывает, что и существующие статические геометрии имели своим основанием именно практику измерения предметов и земельных участков. Но уже в Древнем Египте и, особенно в Древней Греции, геометрия превратилась в «дедуктивную» науку, основывающуюся на нескольких простейших аксиомах, не требующих доказательства. Аксиомы и эмпирические элементы определили в конечном итоге статическую форму отображения геометрией количественных отношений окружающих реальных предметов. Что и стало в последующем атрибутом всех геометрических построений.
Работа начинается с возвращения в математику понятий – «целое», «отдельное» и «безначальное», с последующим рассмотрением диалектических основ современной математики в применении к математическим и геометрическим понятиям и в частности с анализа некоторых принципов и аксиом, на которых основываются геометрии Евклида, Лобачевского и Римана.
Известно, что геометрия как наука была обобщена Евклидом, и его сочинения, включающие 13 томов под названием «Начала», содержали интегрированное изложение всех знаний о геометрии, наработанных античной наукой. Однако смысл «Начал» заключается не только в изложении аксиом и вытекающих из них теорем. «Начала» содержат в неявном виде подход к учению о статической или актуальной бесконечности, с преобладающей опорой на ее статичность.
Статичность актуальной бесконечности, с блеском изложенная Евклидом, на тысячелетия постулировала самой геометрии статичность, полностью исключила даже возможность представления о геометрии как о предмете, изучающем динамическое пространство, застопорила изучение потенциальной бесконечности, стала тормозом в понимании диалектики природы. Она породила другие начала - «Математические начала натуральной философии» И. Ньютона.
«Начала…» Ньютона блестяще развили и закрепили в классической механике принципиальные положения евклидовых «Начал», убрав из механики ее основу, - взаимодействие движущихся тел с пространством, а, следовательно, и само пространство.
Поэтому, когда обнаружилась тройственность аксиомы о параллельных (формулировки Евклида, Лобачевского, Римана), не было сделано предположения о том, что эта тройственность не случайна, а следствие отдельных прорывов в динамику пространства. В пространство движения как взаимодействия вещественных тел с вещественным пространством. И хотя термин «динамика» прижился как раздел механики, изучающей движение тел в зависимости от действующих на них сил, он имеет и другой смысл - подвижности, изменчивости, действенности, напряженности. В последнем смысле термин «динамика» и употребляется в настоящей работе.
Поскольку динамическое пространство имеет отношение к изучению движения и взаимосвязи пространственных свойств и тел в условиях потенциальной бесконечности, то его описание производится путем сопоставления со статическими структурами актуальной бесконечности.
Следует отметить, что и понятие актуальной бесконечности и понятие потенциальной бесконечности есть субъективизация существующей природной бесконечности. О свойствах и движении этой бесконечности нам ничего не известно, но без отображения этих свойств наши теории обходиться не могут.
Другой особенностью русской геометрии является опора в формализации взаимосвязи природных свойств на золотые пропорции. Изучение золотых чисел и золотых пропорций становится модным научным направлением. Однако в этом направлении основным остается изучение взаимосвязей между золотыми числами и описание явлений, в которых встречаются золотые пропорции. Ответов на вопросы: «Какие физические факторы описываются золотыми пропорциями? О чем свидетельствует деление отрезка в крайнем и среднем отношении?» и т.д. еще нет. Поэтому золотые пропорции остаются экзотическим прибавлением к науке и еще не находят широкого применения ни в математике, ни в физике.
Русская геометрия полностью построена на золотых пропорциях. Сама система золотых чисел сведена в матрицы, названные классом русских матриц, взаимозависимость между числами которых оказывается основой теории физической размерности. При этом выяснилось, что все физические свойства тел обладают особыми качественными параметрами числового поля русской матрицы, названные коэффициентами физической размерности, связывающие их в единую систему и обусловливающие формализацию физических уравнений. Последнее обстоятельство коренным образом меняет представление о взаимосвязи физических свойств и формирует единый математический аппарат описания взаимодействия природных свойств во всех разделах физики.
Открытие физической геометрии показало, что существует иерархия геометрий по возможности отображения ими природных процессов. Геометрии в этой иерархии делятся на три предмета:
Физическая (динамическая) геометрия.
Статико-динамическая (полудинамическая) геометрия.
Статические геометрии.
Оказалось также, что статико-динамические геометрии хорошо известны и давно изучаются. Но изучаются как проективные разделы статической геометрии. В них был упущен элемент кадрированного времени, следствием чего и стало одностороннее рассмотрение предмета проективной геометрии.
Работа включает пять глав.
Глава I: Диалектика математики.
Глава II: Динамические свойства геометрии.
Глава III: Золотые пропорции геометрии
Глава IV: Статико-динамическая проективная геометрия.
Глава V: Элементы физической геометрии.
Глава I
Диалектика математики
1.1. Целое и отдельное в познании
Наше понимание целого соответствует пониманию его, изложенному в сутре из «Ишавасья — упанишады»:
«Ом. То есть целое, это тоже целое.
Ибо только целое рождается из целого:
и когда целое отнимается от целого,
смотрите, остаток есть целое.
Ом Шанти, Шанти, Шанти!»
Для дальнейшего понимания наиболее существенным будет:
1. все названные далее целые есть аналоги целого;
2. отсутствие в целом отношений, рождающих как качество-свойство, так и множественность.
Человек пытается познать целое, превращая его в единое путем разделения на познающего и познаваемое. Этим движением создается такое качество-свойство, как отношение. А поскольку исходное отношение – это отношение двух (субъект и объект), то возникает и количество (два) при качественном звучании одного (два рождают одного). В этом мистика чисел у Пифагора и их абсолютизация в современной математике.
Создание отношений всего и со всем есть основной способ познания и основное качество-свойство человеческого ума.
Понятие «целое», является основой науки так же, как и основой религии, но в таком значении в настоящее время практически не осознается. Оно отображает в себе все то, что содержат в неразрывном виде материальный и духовный миры. В этом значении «целое» принадлежит к основаниям философии.
Наука, как и ее отдельные дисциплины, исходит из реальности материального мира, представляющего собой целое другого качества, поскольку исключает духовный мир. Различные направления науки исследуют случайно выделенные свойства-качества, «превращая» целое в единое. Математика изучает количественные аспекты свойств, упуская из внимания единое.
Так что же представляет собой «единое» с позиций современной науки?
Единое − это самодвижимое совокупное всех свойств, не имеющее ни начала, ни конца. Это взаимосвязь бесчисленного количества свойств, образующих многоуровневую субстанцию – материю.
Материя — это целое, «доля» общего, проявившее себя через чувственно воспринимаемое движение. То есть единственным независимым от субъекта (наблюдателя) качеством проявленного единого является чувственно воспринимаемое движение. Остальные качества материи определяются как результат отношения, возникающего при взаимодействии двух тел. Здесь тело при отсутствии отношений есть целое в понимании Вед: отдельное как отношение, и единое как объект познания. Материя, для своего проявления, должна обладать постоянным самодвижением типа пульсации. Самодвижение является атрибутом единого. Отсюда, движением, не требующим двух, может быть только пульсация каждого (любых) из материальных тел.
Пульсация как процесс, через расширение и сжатие носит диалектический характер. Такое движение как неизбежность при смене цикла проходит через прекращение движения (через неподвижность). Неподвижность — это непроявленное единое, которое недостижимо для его проявленного состояния. Тело как совокупность проявленного и непроявленного возникает в момент перехода материального тела через неподвижное состояние при пульсации.
Поэтому понимание телесности (вещественности, материальности) дополняется еще одним представлением субстанции, а именно:
Любое тело это целое, такое же целое, как и весь мир. Отдельность ему создает способ существования, который носит самопринудительный характер и определяется тем, что каждое тело в одном цикле проходит процесс возникновения и исчезновения.
Покажем качественно на примере Земли (рис. 1) точки диапазона существования тела в процессе пульсации. В самом первом приближении Земля пульсирует примерно так же, как и резиновый шар, в котором искусственно и попеременно изменяется давление. В такт изменению давления происходит периодическое увеличение и уменьшение радиуса шара. И так же как у шара, в процессе пульсации Земли возникают две точки останова пульсации: в тот момент, когда радиус шара становится наибольшим 1 и наименьшим 2.

Рис. 1
В момент «останова» материальная поверхность Земли как бы «исчезает», поскольку материя без движения не существует. И всякий останов есть момент «несуществования» материи, т.е. поверхности земного шара (поскольку все полностью остановившееся ни с чем не взаимодействует, ничем не отображается и, следовательно, отсутствует для всего). Все, что имеется в природе и на Земле, приспособлено к этому многоуровневому процессу. В такт пульсации Земли всё обитающее на ней также «ныряет» в небытие (в ничто), изменяясь с возникновением (с началом нового цикла пульсации), и, следовательно, обеспечивая свое материальное бытие. Этим «нырянием» снимается «напряжение», возникающее во всех телах за счет их эволюции (роста, пульсации, расширения), так как эволюция требует изменения материи, а пространства для изменения нет, и потому изменяться и расти некуда. И для того, чтобы процесс эволюции происходил, необходимо всему «встряхнуться», «расшириться», точнее частично «разуплотниться», обусловливая развивающимся (разрастающимся) телам возможность раздвижения разуплотнившейся материи и образования условий дальнейшего роста. И это все также входит в понятие целого. Отметим, что в мире отдельного (в мире тел), статика отсутствует, а все, что ощущается как статика, есть еще не осознанная динамика.
Человек, - мыслящее живое существо, являясь двойственным образованием (тело + душа), подчиняется законам как проявленного, так и непроявленного целого.
Отметим, что основу мышления человека составляет язык, базирующийся на определенных понятиях и словарном запасе, которые дискретны. Эта структура и определяет дискретность нашего мышления. Обучение ребенка языку одновременно становится «дискретизацией» мира, утверждением как бы отдельности всех тел, предметов и явлений путем их языковой символизации. Поэтому реальный мир с детства закрепляется в мышлении как состоящий из отдельных частей и событий, т.е. становится изначально дискретным. Последующие попытки осознания (представления) этого мира как целого оказываются возможными только посредством «сдвигания» вместе отдельных тел, предметов, событий (как частей мира). И в нашем осознанном представлении и даже в интуитивном ощущении возникает понимание целостности как совокупности частей, «склеенных» туманным понятием «связи». «Связи» и обусловливают искусственно сформированному миру иллюзию целого.
Для понимания последующего необходимо применять как самостоятельные следующие понятия: целое, отдельное, единое.
Где:
целое — это то, что не имеет частей и отношений;
отдельное — это отдельные предметы или объекты, тоже целое внутри, а снаружи поверхность как отношение.
единое — это совокупность частей или целых, обладающих качеством и количеством.
Метаморфоза, переводящая материальное целое в отдельное и далее в единое, состоящее из частей, свойств, отношений происходит в момент, когда человек фиксирует что-либо (тело, предмет и т.д.), отличая его от окружающего фона — целого. Эта фиксация состоит из нескольких последовательных операций:
а) выделение тела из фона (целого) как отдельного созданием отношения;
б) узнавание отдельного методом аналогии;
в) наименование (обозначение словом — символом), превращение в единое;
г) наделение целевым признаком, полезным для человека.
Например, геолог в движении фиксирует световую вспышку. Оборачивается и различает блестящее тело (а), приближается к нему и видит камень (б), который определяет как кварц (в). Он знает, что кварц — минерал, который можно использовать в производстве (г).
.
1.2. Отдельное как целое
Являясь целым, человек, единственное из существ, населяющих Землю, потерял ощущение целостности себя и, как результат, не в состоянии воспринимать целостность мира.
Парадокс человеческого мышления заключается в том, что человек пытается примыслить невозможное двойственное:
- отделить себя целиком от всего остального, не замечая, что тем самым переходит в качество дискретности − отдельного;
- сохранить свою целостность со всем остальным, т.е. находиться в качестве сплошности.
Потеря ощущения целостности мира человеком есть следствие его становления как личности, его выделения из природы, его эго. Дуализм субъективного восприятия себя человек целиком переносит на Мир, навязывая ему свои собственные ощущения и представления.
Покажем примерную схему того, как это происходит.
Все психологи знают, что взросление человека носит не столько физиологический характер, сколько психологический и в сущности своей заканчивается как процесс вместе с осознанием себя личностью, т.е. в неявном противопоставлении своего Я всему остальному миру: Я существую как отдельность, и следствие этой отдельности - возникновение антропоцентризма:
Я есть мера всех вещей.
Существую Я и окружающий мир.
Было время, когда меня не было, и будет время, когда Я исчезну.
И т.д. и т.п. …
Отсюда перенос на мир:
Мир состоит из отдельных вещей (тел, объектов).
Каждое тело отделено от другого тела. (Имеет свою форму, свои свойства и т.д.).
Каждое тело когда-то возникло и когда-то исчезнет.
Все в жизни подчинено времени, которое однонаправлено.
И т.д. Каждый может продолжить с любой строчки.
Отсюда, первым телесным качеством становится отдельность. Отдельность (дискретность) нашего мира есть результат внутренней проекции нашего ума. Это не более чем перенос на внешнее (внешний мир) момента осознания своего Я. Не мир изначально состоит из отдельностей, а возникновение внутренней отдельности переносит это ощущение на внешний мир. Поэтому, чтобы получить принципиально другую картину мира, нужно эту проекцию убрать. Психологически в обыденности это трудно, но именно на дискретности (отдельности) основывается вся система математического научного мышления. Оно заменяет «отдельность» как телесное качество безразмерностной категорией «количество», не имеющей никакого отношения к реальности, обусловливая возможность создания таких мыслительных конструкций, которые ничего общего не имеют с реальностью. Субъекты от науки не понимают, что в силу отсутствия диалектических знаний они, своими конструкциями, максимально отображают свое Я. Причем независимо от желания. И в такой хитрой форме, что мир исчезает, а Я остается, и это Я творит, творит то, чему нет никакого соответствия вне Я. То есть Я творит одно из проявлений собственного Я. Но, психологически, Я может сотворить только 1 и/или 2 и их комбинации. Эти цифры и оказываются в основаниях арифметики. Именно поэтому математики со времен Пифагора базировались на цифре 1, не осознавая, что фактически исходят из цифры 2, которая и делает мир дискретным.
Вместе с тем, в математике числа как голой абстракции быть не может уже потому, что число востребуется как элемент объединения разного отдельного по одному качеству – отдельного, и это качество есть конкретное, обособленное и единое для всех предметов, то, что может быть выражено посредством числа или другого знака. То есть:
1 = 1 - если это отдельность или качество, в том числе и формальное (тело, метр, кг, рубль и т.д.)
Теперь, определившись с появлением двух первых чисел арифметического счета, можно поставить вопрос: какая операция является исходной при построении здания арифметики?
Ответ: деление, - потому, что в делении наличествует ликвидация сплошности и абсолютизация дискретности.
«Я» всегда остается в своем мышлении целым (неделимым, монолитным), а все остальное не воспринимается таковым, т.е. является разделенным и, более того, может подвергаться дальнейшему разделению.
Последовательность «разделения»:
 Ситуация А Ситуация А
|
Рис. 2
В ситуации А объект и Я = 1, как отдельные. И по этому качеству и только по этому качеству их можно приравнять 1 = 1. В этом приравнивании отображается их равноправность, равнозначимость т.к. они определяются одним качеством «отдельностью». Но если Я целое и неделимое, то внешний объект таковым не является, поскольку его можно разделить на две части, что показано на рис. 3, где из объекта на рис. 2 получены объекты X и Y.
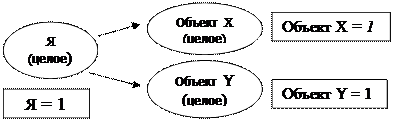 Ситуация Б Ситуация Б
|
Рис. 3
Только в ситуации Б возникает количество, поскольку приравнивание 1(Я) = 1(объект) в ситуации А есть мистическая абсолютизация единицы как неделимого целого. Поэтому, появившись, объект X = 1 и объект Y = 1 уже несут в себе память о предшествующем разделении, что позволяет нам делать операцию сложения 1 + 1 = 2, которая невозможна для ситуации А. И эта память растет с каждым последующим делением как количество.
Отметим, что дробление одного целого на бесчисленные «доли» - новые целые не изменяет количества свойств у новых целых. Они тоже целые, но другие - новые целые, включающие те же свойства, которыми обладало первичное целое, но с иной численной величиной этих свойств и, следовательно, целые другого качества.
Все операции дробления Объекта X и/или Объекта Y можно строго и последовательно повторять еще и еще раз, получая в каждом случае новые объекты, качественно одинаковые по одному признаку - отдельности. И в этой процедуре неявно, как бы аксиоматически, утверждается очевидная для большинства людей (и математиков тоже), но не доказанная вещь, а именно то, что всегда и во всех ситуациях существует равенство: 1 = 1, что далеко не очевидно.
Теперь, разобравшись немного с операцией дробления, мы получили возможность последовательного дробления объекта на части в виде (рис. 4), где повсюду 1 º 1 º 1 º 1… по качеству отдельности:

|
Рис.4.
Попробуем перейти к другой операции, к операции слияния (сложения), предварительно отметив,что деление объекта (дробление) может производиться в любой пропорции (рис. 5), а не только пополам.
Из наших рассуждений мы получили определенный класс объектов, которые равны и равноправны (равнозначны) по одному фундаментальному признаку - по признаку отдельности. Если требование отдельности наложить на реально воспринимаемый нами

Рис. 5
мир (он визуально состоит из отдельных объектов), то сразу получаем чрезвычайно интересный вывод:
В мире отдельных вещей отсутствуют неделимые объекты (более определенно, отсутствуют неделимые кирпичики), и процесс деления любого тела (отдельности) никогда не прекратится (первокирпичик не встретится).
Отметим: данный диалектический анализ проводится для выделения некоторых математических понятий, базирующихся на отдельных природных качествах. Если же рассматривать процесс дробления объектов на отдельности в целом, то следует учитывать и то обстоятельство, что каждая образующаяся отдельность является одновременно и качественно новой отдельностью, отличающейся от остальных численной величиной всех своих качеств и памятью. По этому признаку она всегда является индивидуальностью, не тождественной ни с одной другой индивидуальностью. Если же эти обстоятельства учитывать, то математика как наука никогда бы не возникла.
Как следствие отсутствия первокирпичиков мир отдельных вещей никогда не будет познан. Ибо на каждой ступени концентрации усилий по изучению любой его доли (нового целого) будет сохраняться тождество отдельности: 1 º 1 º 1 º 1 …, то есть будет происходить автоматический откат к исходной отдельности.
Последовательность разделения состоит из нескольких неявных стадий:
Исходное состояние (рис. 6).
 Внимание
Внимание
|
Рис. 6
Субъект выделяет (обращает внимание) на объект Б, если объектов много, или сразу начинает движение к Б.
Промежуточное состояние (сближение) рис. 7: Действие рис. 8:
 
|
Рис. 7 Рис. 8
И результат рис. 9.
|
Рис. 9
Эта процедура разделения обусловлена еще одним диалектическим обстоятельством: разделение происходит в силу невозможности слияния, поскольку в ситуации А (рис. 2.) Я – неделимое целое, а объект Б этим качеством не обладает. Пока рассматриваемый мир не наделен возможностью слияния, он не диалектичен, односторонен и принципиально невозможен как мир, как совокупность единого. Отсюда и возникает необходимость введения в этот мир процесса слияния (соединения) объекта, обратного разделению (разъединению).
Но понимание «простого» слияния скрывает небольшой нюанс, до сих пор явственно не отмеченный в математике. Операция разделения сопровождается образованием отдельностей другого качества. Другое качество отдельностей препятствует их слиянию и «восстановлению» прежнего целого. Получение прежнего целого обусловлено созданием новых условий слияния, и может оказаться так, что не найдется технологии восстановления прежнего целого.
Вернемся к рис.4 и выясним, возможен ли обратный процесс, который переводит его в состояние, отображаемое рис. 2. Логически это сделать нетрудно в следующей последовательности (последовательность действий показана на рис. 10 стрелками).
         
|
Рис. 10
То, что сделано, называется сближением или рядом расположением. Соединение, а тем более слияние, отсутствует по той причине, оно еще не введено в конструкцию. Вводя слияние как противоположность разделению, возвращаемся к конструкции рис 2 (рис. 11).

|
Рис. 11
Из рассмотрения вышеизложенного получаем следствие: Мир, который видится дискретным, состоящим из отдельных тел, таковым не является. В нем присутствует еще одно качество, противоположное дискретности - сплошность. Причем роль этих качеств различна:
дискретность делает мир узнаваемым, позволяя в определенной степени вычленять из мира тела и рассматривать их как отдельные объекты и, прежде всего, вычленять из мира себя (Я и все остальное).
сплошность делает мир целым, телесным, обеспечивая его существование, как и всего, что есть, так и того, чего нет, т.е. нам неизвестного. И, следовательно, никак не может быть воспринят дискретным (отдельным). В сплошности (непрерывности) «отдельное» отсутствует.
Дата добавления: 2015-07-11; просмотров: 193 | Нарушение авторских прав