Читайте также:
|
(модель Леонтьева)
Если считать, что для производства единицы продукции в j -й отрасли требуется aij количество затрат промежуточной продукции i -й отрасли, которое не зависит от объема производства в отрасли, то оно может быть определено как:
; 
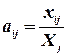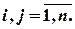
Величины aij называются коэффициентами прямых материальных затрат и характеризуют количество продукции i -й отрасли, использованной при производстве единицы продукции j -й отрасли. Очевидно, что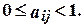 
С учетом коэффициентов aij систему уравнений баланса (9.2) можно переписать в следующем виде:
; 
(9.3)
или в матричном виде:
X=AX+Y, (9.4)
где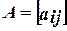 
– матрица коэффициентов прямых материальных затрат;
X, Y – вектор-столбцы валовой и конечной продукции соответственно.
Системы уравнений (9.3) и (9.4) называются ЭММ МОБ Леонтьева, или моделью «затраты – выпуск», за которую В.В. Леонтьев в 1973 г. получил Нобелевскую премию.
С помощью этой модели можно
- определить объемы конечной продукции каждой отрасли Y i, задав в модели величины валовой продукции каждой отрасли X i:
Y=[E – A]X.
- решить обратную задачу, т.е. задав значения Y i, можно определить X i (валовой выпуск продукции):
X=[E – A]-1Y. (9.5)
- задав для ряда отраслей величины валовой продукции, а для всех остальных отраслей – объемы конечной продукции, определить по (9.3) недостающие неизвестные.
Если обозначить B=[b ij ]=[E–A]-1, то (9.5) запишется в матричной форме
X=BY,
где B – матрица коэффициентов полных затрат,
или в виде системы уравнений:
,
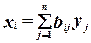где bij – коэффициенты полных материальных затрат, показывающие какое количество продукции i -й отрасли нужно произвести, чтобы с учетом прямых и косвенных затрат этой продукции получить единицу конечной продукции j- й отрасли.
Дата добавления: 2015-07-11; просмотров: 220 | Нарушение авторских прав