
Читайте также:
|
Перейдем к анализу модели МОБ. Коэффициенты прямых затрат по определению являются неотрицательными, следовательно, матрица A в целом может быть названа неотрицательной, т.е. A≥0. Будем называть неотрицательную матрицу A продуктивной, если существует хотя бы один такой неотрицательный вектор X≥0 (вектор валовой продукции), что
X>AX, т.е. [E–A]X>0.
Это определение имеет простой экономический смысл: матрица А продуктивна, если существует такой план X>0, что каждый объект (отрасль, предприятие, цех) может произвести некоторое количество конечной продукции (Y>0).
Продуктивность матрицы может быть определена, если выполняется одно из условий:
1. Матрица [E–A] неотрицательно обратима, т.е. существует обратная матрица [E–A]-1 и все ее элементы неотрицательны.
2. Положительны все главные миноры матрицы [E–A], т.е. определители матрицы, образованные элементами первых строк и столбцов этой матрицы, порядка от 1 до n.
3. Матричный ряд

сходится, причем его сумма равна обратной матрице [E–A]-1.
4. Наибольшее по модулю собственное значение λ матрицы А, т.е. решение характеристического уравнения:
|A–λE|=0,
строго меньше единицы.
Пример 9.1. Оценить продуктивность матрицы

Продуктивность по второму признаку
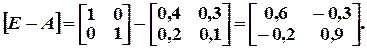
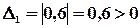
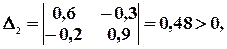 т.е. матрица А продуктивна.
т.е. матрица А продуктивна.
Исходя из того, что кроме прямых затрат существуют косвенные затраты той или иной продукции при производстве продукции данной отрасли, то можно говорить, что коэффициент полных материальных затрат представляет собой сумму прямых затрат и косвенных затрат продукции i -й отрасли для производства единицы продукции j -й отрасли через все промежуточные продукты на всех предшествующих стадиях производства. Если обозначить косвенные материальные затраты различных порядков через A( k ), то в матричной форме матрица коэффициентов полных материальных затрат может быть вычислена как
B=[E–A]-1=E+A+A(1) +A(2)+…
или
 .
.
Обычно этой формулой пользуются для приближенных вычислений. Для точных вычислений используют обратную матрицу [E–A]-1.
Пример 9.2. Для трехотраслевой экономической системы заданы матрица коэффициентов прямых материальных затрат и вектор конечной продукции:

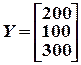 .
.
Найти коэффициенты полных материальных затрат и вектор валовой продукции X, заполнить схему межотраслевого материального баланса.
Матрица полных материальных затрат вычисляется по формуле


Алгоритм нахождения обратной матрицы:
1. Находим [E–A].
2. Составляем вспомогательную матрицу из алгебраических дополнений

3. Транспонируем эту матрицу и вносим в нее определитель
 .
.

Величины валовой продукции трех отраслей определим по формуле

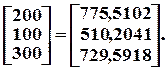
Межотраслевые потоки продукции рассчитываем по формуле
 ,
, 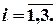
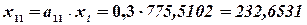
 и т.д.
и т.д.
Заполняем таблицу межотраслевого баланса (табл. 9.2).
Таблица 9.2
Дата добавления: 2015-07-11; просмотров: 67 | Нарушение авторских прав