Программа выполнения работы

2.1 ЗАДАЧА 4.1. СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ И КОЛИЧЕСТВО ПОЛОЖИТЕЛЬНЫХ ЭЛЕМЕНТОВ

Написать программу, которая для целочисленной матрицы 10х20 определяет сред­нее арифметическое ее элементов и количество положительных элементов в каж­дой строке.

Алгоритм решения этой задачи очевиден. Для вычисления среднего арифметиче­ского элементов массива требуется найти их общую сумму, после чего разделить ее на количество элементов. Порядок просмотра массива (по строкам или по стол­бцам) роли не играет. Определение количества положительных элементов каждой строки требует просмотра матрицы по строкам. Обе величины вычисляются при одном просмотре матрицы. Блок-схема этого алгоритма приведена на рис. 2.

Размерности массива заданы именованными константами, что позволяет легко их изменять. Для упрощения отладки рекомендуется задать небольшие значения этих величин или приготовить тестовый массив в текстовом файле и изменить програм­му так, чтобы она читала значения из файла (см. задачу 4.2).

Составляйте тестовые примеры таким образом, чтобы строки массива содержали разное количество отрицательных элементов (ни одного элемента, один и более элементов, все элементы).

При вычислении количества положительных элементов для каждой строки вы­полняются однотипные действия: обнуление счетчика, просмотр каждого элемен­та строки и сравнение его с нулем, при необходимости увеличение счетчика на единицу, а после окончания вычислений – вывод результирующего значения счетчика. Впрочем, это дольше описывать на естественном языке, чем в про­грамме.

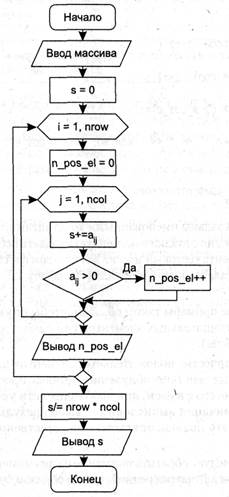
Рис. 2. Блок-схема алгоритма решения задачи 4.1

#iinclude <iostream.h>

#include <iomanip.h>

void main(){

const int nrow = 10, ncol = 20;

int a[nrow][ncol];

int i, j;

cout << “Введите элементы массива:” << endl;

for (i = 0; i < nrow; i++)

for (j =0; j < ncol; j++) cin >> a[i][j];

for (i = 0; i < nrow; i++) {

for (j = 0; j < ncol; j++) cout << setw(4) << a[i][j] << “ “;

cout << endl;

}

int n_pos_el;

float s = 0;

for (i = 0; i < nrow; i++) {

n_pos_el =0;

for (j = 0; j < ncol; j++) {

s += a[i][j];

if (a[i][j] > 0) n_pos_el++;

}

cout << “ Строка: “ << i << “ кол-во: “ << n_pos_el << endl;

}

s /= nrow * ncol;

cout << “Среднее арифметическое: “ << s << endl;

}

Тем не менее, здесь следует обратить внимание на два момента. Во-первых, требу­ется еще до написания алгоритма решить, каким образом будут храниться результаты. Со средним арифметическим все ясно, для его хранения необходима одна простая переменная вещественного типа. А вот количество положительных эле­ментов для каждой строки свое, и в результате мы должны получить столько зна­чений, сколько строк в матрице. В данной задаче мы можем отвести для хранения этих значений одну-единственную переменную целого типа, поскольку они вычисляются последовательно, после чего выводятся на экран. Однако в других за­дачах эти значения могут впоследствии потребоваться одновременно. В этом случае для их хранения придется описать целочисленный массив с количеством элемен­тов, равным количеству строк матрицы.

Второй важный момент – место инициализации суммы и количества. Сумма об­нуляется перед циклом просмотра всей матрицы, а количество положительных элементов – перед циклом просмотра очередной строки, поскольку для каждой строки его вычисление начинается заново. Начинающие часто либо вообще забы­вают про инициализацию накапливаемых в цикле величин, либо неверно опреде­ляют ее место в программе.

СОВЕТ: Записывайте операторы инициализации накапливаемых в цикле величин непосредственно перед циклом, в котором они вычисляются.

После ввода значений предусмотрен их контрольный вывод на экран. Для того чтобы элементы матрицы располагались один под другим, используется манипу­лятор setw(), устанавливающий для очередного выводимого значения ширину поля в четыре символа. Для использования манипулятора необходимо подключить к программе заголовочный файл <iomanip. h>. После каждой строки выводится сим­вол перевода строки endl.

При написании вложенных циклов следите за отступами. Все операторы одного уровня вложенности должны начинаться в одной и той же колонке. Это облегчает чтение программы и, следовательно, поиск ошибок. По вопросу расстановки фи­гурных скобок существуют разные мнения специалистов. В настоящее время наи­более распространенными являются два стиля: стиль 1TBS (OneTrue Bracing Style), которого придерживались основоположники языка С – Б. Керниган (Brian Kerni-ghan) и Д. Ритчи (Dennis Ritchie), и стиль Алмена (Eric Allman). Приведем отры­вок кода, написанного в стиле 1TBS:

for (j = 0; j < MAX_LEN; j++) {

foo();

}

Этот же отрывок в стиле Алмена выглядит так:

for (j = 0: j < MAX_LEN; j++)

{

foo();

}

Наш выбор, естественно, остановился на единственно верном стиле.

Дата добавления: 2015-07-11