Работа № 17 Определение теплопроводности газов методом нагретой нити

Между двумя телами, разделенными газовым промежутком и имеющими разные температуры, происходит теплообмен, который обусловлен тремя процессами: теплопроводностью, конвекцией и лучеиспусканием (тепловым излучением).

Теплопроводность газов – это перенос энергии за счет химического (теплового) движения молекул. Скорость такого движения зависит от температуры. Молекулы газового слоя, прилегающему к горячему телу, обладают большей скоростью, и следовательно, энергией. Благодаря взаимным столкновениям эта энергия передастся молекулам соседних слоев газа. В результате в газовом слое, прилегающем к холодному телу, энергия молекул возрастает и при столкновении с телом молекулы передают ему часть своей энергии. Таким образом, происходит перенос энергии от горячего тела к холодному.

Конвекция – это перенос энергии (тепла) за счет перемещения частей газа как целого. Теплый газ поднимается вверх, а на его место опускаются более холодные массы газа. Конвекция не возникает, если температура газа повышается с высотой или если объем газа невелик.

Лучеиспускание заключается в излучении телами электромагнитных волн.

В условиях данной работы конвекцией и тепловым излучением можно пренебречь. Поэтому дальше мы будем рассматривать только процесс теплопроводности.

Если газ неравномерно нагрет, т.е. температура в одной его части выше или ниже, чем в другой, то возникает поток тепла от мест с большей температурой к местам с меньшей температурой. Рассмотрим одномерный случай, когда температура газа меняется в направлении X, например увеличивается (рис.1).

На основе обобщения опытных данных был установлен эмпирический закон для потока тепла (закон Фурье).

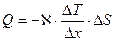
Здесь Q – поток тепла, т.е. количество энергии переносимой через площадку 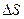за единицу времени. 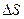- площадь площадки расположенной между слоями с координатам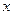и и 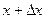перпендикулярно оси x, 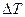- разность температуры между этими слоями, 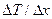- градиент температуры, æ – коэффициент теплопроводности, зависящий от рода газа и от условий в которых газ находится. Знак ''-'' означает, что поток тепла направлен в сторону убывания температуры.

В тех случаях, когда газ, в котором существует градиент температуры, предоставлен самому себе, т.е. к нему извне не подводится энергия, теплопроводность приводит к выравниванию температуры. Это нестационарная теплопроводность.

Если же подводить к газу тепло извне, то можно искусственно поддерживать разность температур постоянной. Это стационарная теплопроводность. В этих условиях количество тепла, протекающего через газ в единицу времени равно мощности источника энергии, за счет которого поддерживается заданный градиент температуры, эта мощность (обычно электрическая) и подлежит измерению при экспериментальном определении коэффициента теплопроводности.

Одним из наиболее распространенных методов измерения коэффициента теплопроводности газов является метод нагретой нити.

Рассмотрим идею этого метода.

Исследуемым газом заполняют пространство между двумя коаксинальными цилиндрами с радиусом r₁ и r₂ (рис.2). Внутренний цилиндр представляет собой просто тонкую проволоку, по которой пропускается электрический ток, что она служит и нагревателем, потребляющим мощность P. Другой цилиндр охлаждается так, чтобы его температура T₂ оставалась все время постоянной.

Через некоторое время после включения нагревателя устанавливается стационарное состояние, при котором температура T₁ внутреннего, нагревательного цилиндра тоже становиться постоянной. Тем самым, между внутренним и внешним цилиндрами, установится постоянная разность температур T₁-T₂ . Величина этой разности температур зависит от теплопроводности газа. Найдем эту зависимость.

Если длина цилиндра равна R, то количество тепла, протекающее в 1с через любое цилиндрическое сечение S радиуса r (т.е. 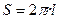) определяется уравнением

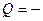æ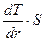

где dT/dz – градиент температуры вдоль радиуса цилиндра. Если высота цилиндра достаточно велика по сравнению с радиусом, то температуру вдоль оси цилиндра можно считать повсюду одинаковой.

В стационарном состоянии Q равно мощности нагревателя P.

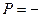æ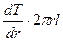

Отсюда

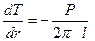или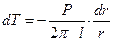

Интегрируя получаем

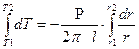
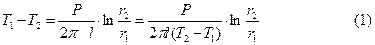
Все величины входящие в эту формулу могут быть измерены. Электрическая мощность P, выделенная в нити, может быть вычислена по закону Джоуля-Ленца.

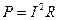
где 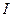-сила тока протекающего по нити, R-сопротивление нити (проволоки). Наибольшую трудность вызывает измерение температуры нагретой нити (T₁) она определяется по изменению сопротивления нити и может быть рассчитана по формуле

где t_н – температура нити (⁰С)

t_к – комнатная температура (20 ⁰С)

- температурный коэффициент сопротивления

R₀ – сопротивление нити при комнатной температуре

R – сопротивление нагретой нити

Дата добавления: 2015-07-11