Спектральное представление периодических сигналов

Периодический сигнал с периодом Т, который описывается некоторой функцией у(х), отвечающей условиям Дирихле, можно представить в виде ряда Фурье:

,

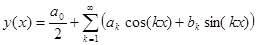где а₀/2- постоянная составляющая;

a_k, b_k- коэффициенты ряда Фурье.

Коэффициенты определяются для абсолютно интегрируемой на отрезке [-p; p] функции у(х) по формулам Эйлера-Фурье:

;

.

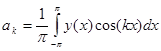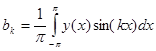В приведенных выражениях х может иметь размерность времени(t).

Часто, особенно в радиотехнических расчетах, периодические сигналы представляются как функции времени y(t) на отрезке [0, T] с периодом Т=1/f₁, где f₁-частота первой гармоники периодического сигнала. В этом случае ряд Фурье представляется в виде:

,

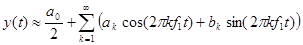где ;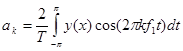

.

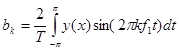В этом случае коэффициенты a_k и b_k описывают косинусную и синусную составляющие k-ой гармоники сигнала с периодом Т и частотой f₁=1/T.

Часто используется иная форма ряда Фурье (особенно при синтезе различных сигналов):

,

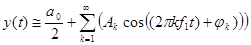или при использовании общепринятых обозначений:

,

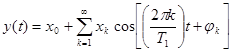где 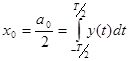- постоянная составляющая сигнала;

x_k=A_k- амплитуда k-й гармоники;

k- номер гармоники;

;

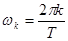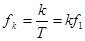- частота k-й гармоники;

j_k- фаза k-й гармоники.

Как видно из выражений, периодический сигнал y(t) представляется как сумма бесконечно большого числа гармонических составляющих с амплитудами x_k, частотами f_k и фазами j_k.

Разложение функции на гармонические составляющие, то есть вычисление коэффициентов Фурье, называется гармоническим или спектральным анализом. Воссоздание функции, представленной рядом Фурье, называют спектральным синтезом.

Гармонику с k=1 называют основной или первой гармоникой сигнала. Она задает его частоту повторения f₁. Остальные гармоники называют высшими из частных. Они определяются как f_k=k×f₁, k=2, 3, 4, …

Таким образом, спектр периодических сигналов, представимых рядом Фурье, дискретный, то есть он содержит набор фиксированных частот f_k, где k=1, 2, 3,…. Для непериодических сигналов спектр будет сплошным.

Определение: совокупность величин x_k есть спектр амплитуд, совокупность величин j_k- спектр фаз.

При анализе реальных процессов x_k можно определить как:

.

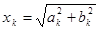На рис. 37 представлены примеры некоторых периодических сигналов и их спектров.

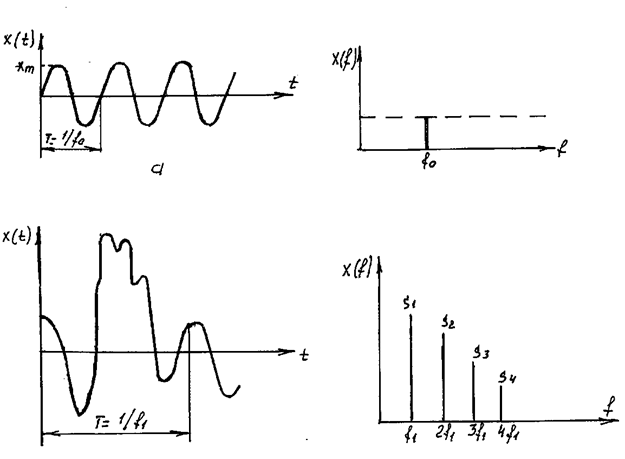
Рис. 37. Примеры некоторых периодических сигналов и их спектров: а – для гармонического процесса; б – для полигармонического процесса (сумма 4-х синусоид)

Для анализа дискретных сигналов в частотной области используют дискретное преобразование Фурье.

При дискретизации времени непрерывный сигнал x(t) преобразуется в последовательность дискретных выборок (рис. 38).

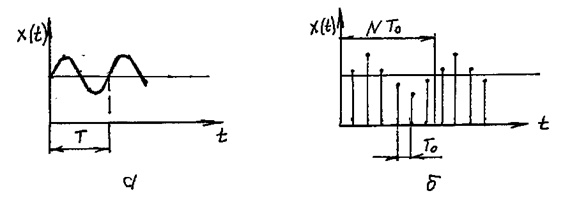
Рис. 38. Пример дискретизация времени: а – непрерывный сигнал; б – последовательность дискретных выборок

Если выборки осуществляются регулярно через интервал времени Т₀, то получается последовательность x_n(iT₀), где i=0, 1, 2,…,N-1. Общая длительность сигнала T=N×T₀.

Полагают, что функции x_n(iT₀) и S_n(RDf) связаны парой дискретного преобразования Фурье (ПДФ):

— прямого:

;

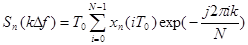— и обратного:

.

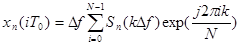При этом T₀Df=1/N.

Так же по аналогии с интегралом Фурье записывают дискретные преобразования в виде:

;

,

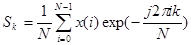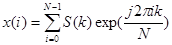где ;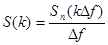

x(i)=x_n(iT₀)- i-я выборка последовательности значений сигнала.

Это выражения часто используют при построении алгоритмов обработки дискретных сигналов.

Однако, вычисления, проводимые при выполнении ДПФ, довольно громоздки; они требуют примерно N² арифметических операций. Для ускорения преобразования разработаны специальные алгоритмы, значительно сокращающие объем и продолжительность вычислительных операций. Эти алгоритмы называют БПФ.

К спектральным характеристикам, используемым на практике, относятся также текущий и мгновенный спектры. Согласно выражению:

,

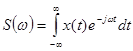для каждого спектра сигнала x(t) необходимо выполнить интегрирование по времени в бесконечных пределах. Но реальные физические процессы обычно исследуются в течение конечного времени, и, следовательно, интегрирование ведется в пределах от момента начала наблюдения до данного, текущего момента t.

Тогда спектр примет вид:

.

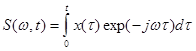Функция S(w, t) является функцией не только частоты, но и времени и называется текущим спектром.

Это понятие важно для теории и техники анализа спектра. Дело в том, что периодичность процесса проявляется лишь за достаточно большое время,– по крайней мере, за несколько периодов (рис. 39).

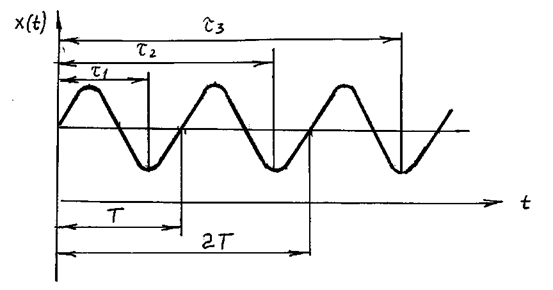
Рис. 39.

В течение же небольшой части периода характерные черты процесса вырисоваться не успевают. Спектр короткого отрезка процесса– сплошной, так как этот отрезок по существу является коротким импульсом (рис. 40). Переход к линейчатому спектру происходит лишь в пределе, когда t®µ (строго теоретически); на практике оказывается достаточной при условии t=nT (n>>1).

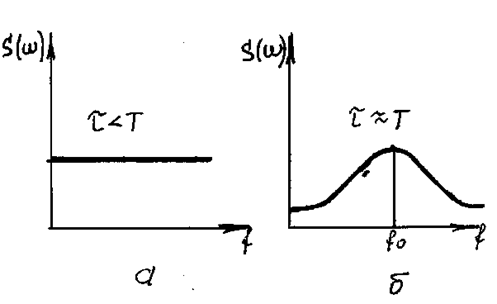
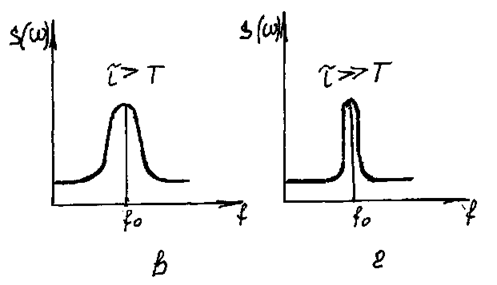
Рис. 40.

Мгновенный спектр описывается функцией:

,

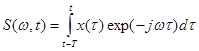и определяется как спектр отрезка сигнала длительностью Т, непосредственно предшествующего данному моменту t. В частности, мгновенный спектр нужно рассматривать как разность двух текущих спектров, то есть как приращение текущего спектра за интервал времени Т.

,

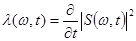где S(w, t)- текущий спектр.

Дата добавления: 2015-07-11