
Читайте также:
|
В предыдущих лекциях рассматривалось представление сигналов во временной области, то есть значения сигналов рассматривались как функции времени. Для решения ряда задач целесообразно пользоваться представлением сигналов в частотной области, опираясь на зависимость значений или определенных параметров сигнала от частоты. Иначе это представление называют спектральным представлением. Оба вида представления взаимосвязаны, то есть данной функции во временной области всегда существует единственная функция в частотной области, и целесообразность выбора вида представления сигнала определяется характером и условиями решения задачи.
Характеристики, описывающие свойства сигнала при частотном представлении, называют спектральными. Наиболее полными характеристикам служат частотные спектры (амплитуд, мощности, фаз). Для оценки степени нелинейных искажений, претерпеваемых синусоидальным сигналом при прохождении через нелинейную цепь, используют коэффициент гармоник. Также к спектральным характеристикам относят КЕПСТР, девиацию частоты ЧМ сигнала и некоторые другие характеристики.
Аппаратурно задача спектрального анализа решается с помощью специальных приборов– анализаторов спектра.
Перевод некоторого сигнала x(t) из временного представления в частотное осуществляется относительно просто с помощью преобразований Фурье. Так, например, для абсолютно интегрируемой функции x(t) достаточно вычислить интеграл Фурье:
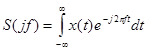 ,
,
где комплексная функция S(jf)- спектральная плотность амплитуд процесса x(t).
Это преобразование справедливо для детерминированных процессов. Так же его можно применить и к анализу конкретной реализации случайного процесса как к неслучайной функции времени.
Дата добавления: 2015-07-11; просмотров: 60 | Нарушение авторских прав