Читайте также:
|
Напомним, что об эффективном кодировании уже шла речь в подразделе 5. Основные моменты сводятся к следующему:
- идея такого кодирования базируется на том, чтобы использовать для часто встречающихся символов более короткие кодовые цепочки, а для редких - более длинные. В результате средняя длина кода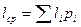 
будет меньше, чем при равномерном кодировании;
- согласно теореме Шеннона, наилучшее кодирование позволяет сократить lср. до величены энтропии Н, подсчитанной для данного набора символов;
- добавим, что неравномерное кодирование позволяет автоматически устранить избыточность, связанную с тем, что количество символов в алфавите может быть не кратно степени двойки (так, например, чтобы закодировать одинаковым числом разрядов 5 разновидностей символов потребуется 3 бита, так же как и для 8 символов).
Идея неравномерного кодирования, в котором длина кодовой цепочки зависит от частоты появления соответствующего символа, реализована еще в знаменитой «азбуке Морзе». Однако там наряду с «точками» и «тире» использовался третий кодовый символ – разделитель «пауза». Если ограничиться только «O» и «1», то при построении кода необходимо учесть дополнительное требование: чтобы все кодовые цепочки однозначно выделялись в непрерывном потоке битов, ни одна из них не должна входить как начальный участок в кодовую, цепочку другого символа. Такое свойство кода называется префиксностью.
Наибольшее распространение получил способ построения эффективного кода предположенный Хаффманом. Рассмотрим его на примере. Пусть задан алфавит из 5 разновидностей символов Z1 – Z5, и их вероятности. В таблице 6.1 наряду с этими исходными данными приведены так же результаты кодирования по Хаффману: кодовые цепочки Ki их длинны li. Процедуру построения кода иллюстрирует таблица 6.2 и рисунок 5
Пример кода Хаффмана
Таблица 6.1
| Zi | Pi | Ki | li |
| Z1 Z2 Z3 Z4 Z5 | 0,25 0,17 0,08 0,35 0,15 | ||
| lср |
Объединение вероятностей символов
Таблица 6.2
| Zi | Pi | Шаги объединения | Ki | |||
| Z1 Z2 Z3 Z4 Z5 | 0,35
 0,25
0,17
 0,15
0,08
|  0,35
0,25
 0,23
0,17
|  0,40
 0,35
0,25
|   0,60
0,40
| 1,00 |
На первом этапе символы упорядочивают по убыванию вероятностей, а затем выполняют несколько шагов «объединения», на каждом из которых суммируются вероятности наиболее редко встречающихся символов и столбец вероятностей пересортировывается (см. табл.6.2).
На втором этапе строится «дерево кода», ветви которого отображают в обратном порядке процесс «объединения вероятностей». При построении дерева принимается правило соответствия большей вероятности одному из направлений ветви (например «левому») и определенному значению бита кода (например, «1») (рис.5). Цепочки битов от «корня» до конца каждой ветви соответствуют кодам исходных символов (табл.6.1 – 6.2).
| В табл.6.2 наглядно видны следующие закономерности кода: - часто встречающиеся символы получили более короткие кодовые цепочки. В частности, за счет этого средняя длина цепочки составила lср = 2,23, что значительно меньше, чем lср = 3,00 при равномерном кодировании; - ни одна из цепочек не входит как начальный участок в другую (выполняется так называемое правило «префиксности», благодаря чему коды символов легко можно выделить в потоке битов. |
Рис.5 «Дерево кода» по Хаффману
Процедура кодирования сводится к выбору из кодовой таблицы цепочек, соответствующих каждому символу источника. Декодирование предусматривает выделение в битовом потоке кодов символов и их расшифровку в соответствии с таблицей. Пример показан на рис.6.
Передаваемые символы Z1, Z2, Z3, Z4, Z5
Битовая последовательность 00 11 10 011 111
Принятые символы Z1*, Z2*, Z3*, Z4* , Z5*
(результат декодирования)
Рис.6 Пример кодирования и декодирования по Хаффмену
Код Хаффмена может быть двухпроходным и однопроходным. Первый строится по результатам подсчета частот (вероятностей) появления различных символов в данном сообщении. Второй использует готовую таблицу кодирования, построенную на основе вероятностей символов в сообщениях похожего типа. Например, кодирование текста на русском языке в первом случае включает его предварительный анализ, подсчет вероятностей символов, построение дерева кода и таблицы кодирования индивидуально для данного сообщения. Во втором случае будет работать готовая таблица, построенная по результатам анализа множества русскоязычных текстов. Двухпроходный код более полно использует возможности сжатия. Однако, при этом вместе с сообщением нужно передавать и кодовую таблицу. Однопроходный код не оптимален, однако прост в использовании, поэтому на практике обычно применяют именно его.
В целом код Хаффмена проигрывает по сравнению с «цепочечными» кодами и его редко используют самостоятельно, однако он часто фигурирует как элемент более сложных алгоритмов сжатия.
Очевидно, что посимвольное кодирование не использует резервы сжатия информации, связанные с повторяемостью цепочек символов. Так например, в исходном тексте программы на алгоритмическом языке часто встречаются повторяющиеся наименования операторов или идентификаторы, которые в принципе можно закодировать короткими битовыми последовательностями.
Наиболее удачным алгоритмом сжатия, основанным на таком подходе является алгоритм Лемпеля-Зива, который в разных модификациях используется, в частности, в большинстве программ-архиваторов. Основная идея алгоритма состоит в том, что цепочки символов, уже встреченные ранее кодируются ссылкой на их «координаты» (номер первого символа и длину) в «словаре», где находится уже обработанная часть сообщения.
Суть его в следующем: упаковщик постоянно хранит некоторое количество последних обработанных символов в буфере. По мере обработки входного потока вновь поступившие символы попадают в конец буфера, сдвигая предшествующие символы и вытесняя самые старые. Размеры этого буфера, называемого также скользящим словарем (sliding dictionary), варьируются в разных реализациях (в LHarc 1.13 используется 4-килобайтный буфер, LHA 2.13 и PKZIP 1.10 - 8-килобайтный, а ARJ 2.20 - 16-килобайтный).
Алгоритм выделяет (путем поиска в словаре) самую длинную начальную подстроку входного потока, совпадающую с одной из подстрок в словаре, и выдает на выход пару (length, distance), где length - длина найденной в словаре подстроки, а distance - расстояние от нее до входной подстроки (то есть фактически индекс подстроки в буфере, вычтенный из его размера). В случае, если такая подстрока не найдена, в выходной поток просто копируется очередной символ входного потока.
В первоначальной версии алгоритма предлагалось использовать простейший поиск по всему словарю. Время сжатия при такой реализации было пропорционально произведению длины входного потока на размер буфера, что непригодно для практического использования. Однако, в дальнейшем было предложено использовать двоичное дерево для быстрого поиска в словаре, что позволило на порядок поднять скорость работы алгоритма.
Таким образом, алгоритм Лемпеля-Зива преобразует один поток исходных символов в два параллельных потока length и distance. Очевидно, что эти потоки являются потоками символов в новых алфавитах L и D, и к ним можно применить один из упоминавшихся выше методов (RLE, кодирование Хаффмана, арифметическое кодирование). Так мы приходим к схеме двухступенчатого кодирования, наиболее эффективной из практически используемых в настоящее время (и, в частности, использованной автором). При реализации этого метода необходимо добиться согласованного вывода обоих потоков в один файл. Эта проблема обычно решается путем поочередной записи кодов символов из обоих потоков.
Уточним дополнительно некоторые моменты:
- коды координат цепочки и коды отдельных символов различаются битовыми признаками (например, в первом случае – 1, во втором –0);
- поскольку цепочки находятся чаще в начале словаря, и чаще бывают короткими, дополнительный выигрыш получают за счет статистического кодирования (по Хаффмену) их «адресов» и «длин»;
- «канал» - понятие применимое и к реальному каналу передачи данных, и к файлу, куда данные записываются для хранения. В последнем случае декодер «отрабатывает» при разворачивании сжатого файла;
- при ограниченной длине словаря (обычно от 4 до 16 кбайт) новые поступающие символы и цепочки «вытесняют» прежние (текст как бы «вдвигается» в словарь). Разумеется, вначале, когда словарь не заполнен, эффективность сжатия невысока. Рост объема словаря позволяет повысить степень сжатия, но значительно увеличивается трудоемкость поиска цепочек.
Добавим, что алгоритм Лемпеля-Зива используется в большинстве популярных программ-архиваторов (в том числе, например, в zip, rar, arj и их windows – версиях). Различие скорости и эффективности кодирование-декодирование определяются в основном особенностями программной реализации.
Алгоритм Лемпеля-Зива требует большого количества вычислительной работы. Его модификация - алгоритм Лемпеля-Зива-Велча является менее трудоемким, хотя и дает несколько худшие результаты по сжатию.
Алгоритм упаковки Лемпеля-Зива-Велча (Lempel-Ziv-Welch compression, LZW) работает так. Будем предполагать, что входной алфавит состоит из m различных символов.
1. Инициализация словаря. В пустой словарь помещаются все m различных односимвольных строк.
2. Строке P, называемой "префиксом", присваиваем пустое значение.
3. Пусть k - очередной символ входного потока.
4. Ищем строку P+k в словаре.
Если нашли, то P:= P+k,
сдвигаем указатель входного потока на следующий символ,
переходим к п. 3.
иначе
выводим номер строки P в словаре в выходной поток,
добавляем строку P+k в словарь,
P:= k (строка длины 1),
сдвигаем указатель входного потока на
length(P) символов,
переходим к п.3
конец_если.
Дата добавления: 2015-07-10; просмотров: 223 | Нарушение авторских прав