Метод сжатия Хаффмена

Алгоритм Хаффмена предлагает отказаться от обычного представления файлов в виде последовательности 8-битных символов. Главный недостаток такого способа хранения данных состоит в том, что в нем не делается различий между кодированием символов, с различной частотой встречающихся в файлах. Так, наиболее часто встречающиеся в английском языке буквы E и I имеют ту же самую длину, что и относительно редкие Z, X или Q.

Один их первых алгоритмов эффективного кодирования информации был предложен Д.А.Хаффменом в 1952 г. Идея алгоритма состоит в том, что, зная вероятности вхождения символов в сообщение, можно описать процедуру построения кодов переменной длины, состоящих из различного количества битов. Символам, которые чаще встречаются в сообщении, присваиваются более короткие коды. Коды Хаффмена имеют уникальный префикс, что и позволяет однозначно их декодировать, несмотря на их переменную длину.

Простейший способ кодирования информации символами переменной длины осуществляется при помощи таблицы соответствия. Например, анализируя любой английский текст, можно установить, что буква E встречается гораздо чаще, чем Z, а буквы X и Q относятся к наиболее редко встречающимся. Таким образом, используя статистические данные, можно составить таблицу соответствия, в которой буква E закодируется меньшим числом бит, а буквы X и Q - более длинными кодовыми последовательностями. Хотя такой прием пригоден для текстов любого типа, большинство практических программ вычисляют свою таблицу соответствия для каждого нового файла. Таким образом, исключаются случайные отклонения каждого конкретного файла от среднестатистического, и устраняются связанные с этим потери эффективности сжатия.

Классический алгоритм Хаффмена вначале определяет таблицу частот встречаемости символов и на основании нее строится дерево Хаффмена.

В целом алгоритм кодирования Хаффмена включают следующие этапы:

1. Подсчитываются частоты встречаемости всех символов исходного файла.

2. Полученный список символов сортируют в порядке убывания частоты повторения символов. В результате все символы входного файла образуют упорядоченный список свободных узлов (листов дерева). Каждый узел имеет вес, равный количеству вхождений символа в исходное сообщение.

3. Выбираются два свободных узла дерева с наименьшими весами.

4. Создается их родитель с весом, равным их суммарному весу.

5. Новый родитель добавляется в список свободных узлов, а двое его детей удаляются из этого списка.

6. Одной дуге, выходящей из родителя, ставится в соответствие бит 1, а другой - бит 0.

7. Шаги, начиная со второго, повторяются до тех пор, пока в списке свободных узлов не останется только один свободный узел. Он и будет считаться корнем дерева.

Пример 8.

Исходный файл:

Таблица 16

ABAACCC

N₀ =7 байтов = 56 битов.

После выполнения первых двух шагов алгоритма Хаффмена получим упорядоченный список символов и частот их повторений (табл. 17).

Таблица 17

Символ (узел)	A	C	B
Частота повторения (вес)

Далее выбираются узлы C и B, имеющие наименьшие веса, и создается новый родитель CB с суммарным весом, равным 4 (рис. 1)

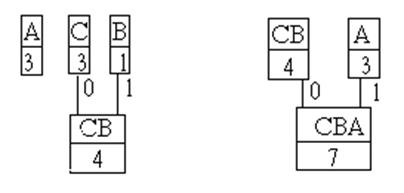
Рис. 1 Рис. 2

После этого остаются свободными узел A и новый узел CB, которые после сортировки образуют новый узел CBA (рис. 2). Т.к. он является единственным оставшимся свободным узлом, то на этом процесс построения дерева кодирования Хаффмена заканчивается. Заметим, что вес последнего узла CBA, являющегося одновременно корнем дерева Хаффмена, точно равен числу символов в исходном файле.

Чтобы определить код для каждого символа, входящего в сообщение, нужно пройти путь от узла дерева, соответствующего этому символу, до корня дерева, накапливая биты при перемещении по ветвям дерева. Полученная таким образом последовательность битов является кодом данного символа, записанным в обратном порядке (табл. 18).

Таблица 18

Символ	Двоичный код Хаффмена
A
B
C

Тогда сжатый файл будет представлять собой комбинацию битов:

Таблица 19

N₁= 11 битов; K_сж= N₁/N₀= 11/56 = 0.2.

Рассмотрим старый пример 3.

Исходный файл:

Таблица 20

X=5.2*******Y=5.********C=0********D=4.

Последовательность выполнения этапов построения дерева Хаффмена изображена на рис. 3а,б,в,г,д

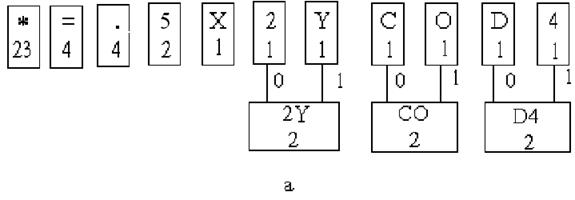
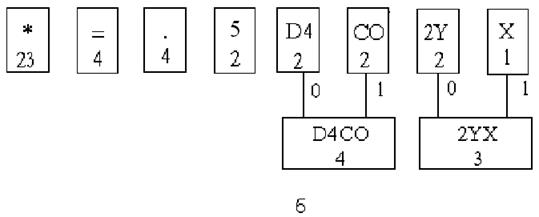
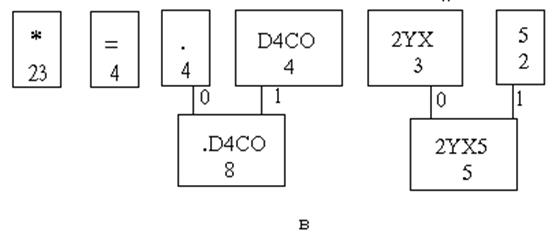
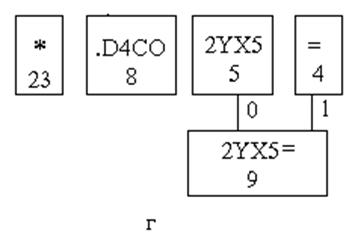
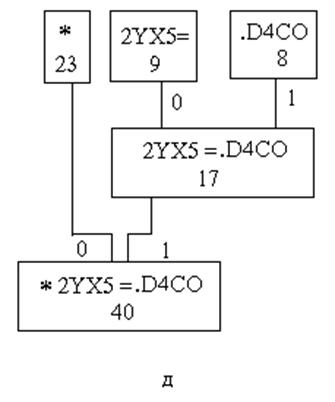
Рис. 3

Коды Хаффмена всех символов данного файла приведены в табл. 21.

Таблица 21

Символ	Двоичный код Хаффмена
*
=
.
X
Y
C
O
D

Из нее видно, что ни один код не является префиксом другого кода. Двоичный сжатый файл представлен в табл. 22. Однако минимальной единицей измерения информации является байт. Поэтому весь сжатый двоичный файл разбивается на группы по восемь битов, каждая из которых соответствует определенному ASCII символу. В рассматриваемом примере для образования последней группы символов не хватило четырех битов. Вместо них можно добавить любые заранее оговоренные значения, например нули. Для рассматриваемого примера N₁= 92 бита; K_сж = N₁/N₀= 92/320 = 0.3.

Таблица 22

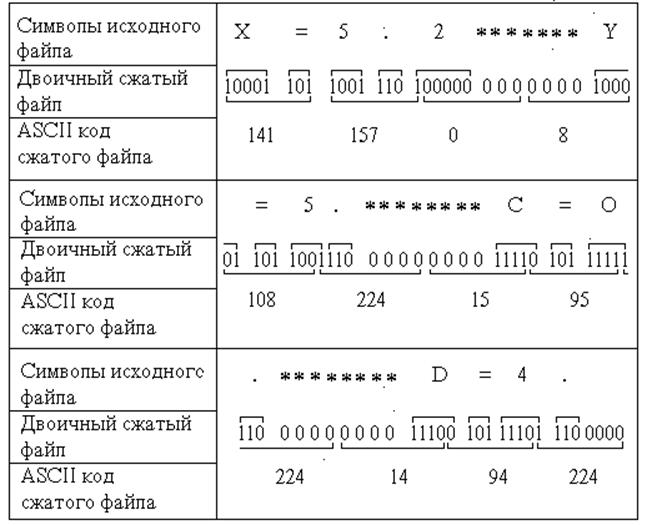
Однако для восстановления исходного сообщения недостаточно иметь только сжатый файл. Декодер должен знать либо таблицу частот повторения всех символов исходного сообщения, либо коды Хаффмена всех символов, встречающихся в исходном файле. Следовательно, длина сжатого файла увеличится на длину таблицы частот или кодов символов.

Рассмотрим случай, в котором в начале сжатого файла указываются коды Хаффмена всех символов исходного файла. Тогда структура сжатого файла может выглядеть следующим образом:

Таблица 23

nMS₁l₁S₂l₂.....S_Ml_MH₁H₂......H_MF

где n - число двоичных разрядов, добавленных в конец сжатого файла F, чтобы его длина N₁ представлялась числом, делящимся на 8 без остатка, 0 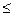n 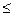7; M - число различных символов, встречающихся в исходном файле, 0 < M 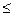255; S_i - ASCII код i-го символа исходного файла, i =1, …,M; l_i - число битов кода Хаффмена символа S_i; H_i - код Хаффмена символа S₁; F - собственно сжатый файл.

Тогда для последнего примера полный сжатый файл представлен в табл. 24.

Таблица 24

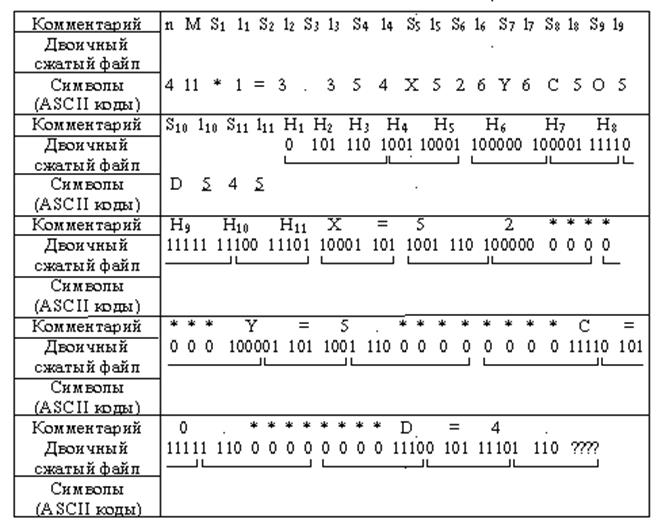
N₁= 42 байта; K_сж= N₁/N₀ = 42/40 = 1.05.

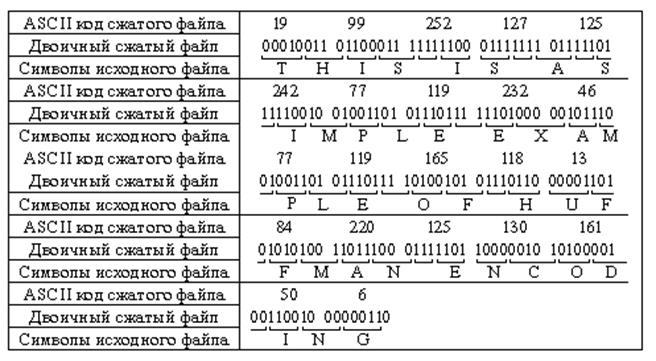
Рассмотрим пример по декодированию сжатого файла.

Пример 9

Сжатый файл:

Таблица 25

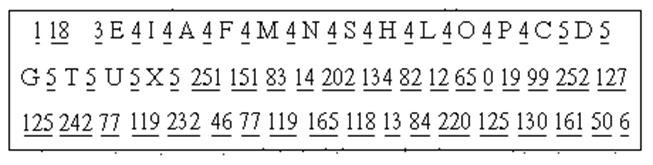
Первый символ ASCII 1 означает, что из последнего байта сжатого файла один последний бит следует выбросить, т.к. он был добавлен при сжатии, т.е. n=1.

Второй символ сжатого файла ASCII 18 показывает, что в исходном файле имелось 18 различных символов, т.е. M=18. Следовательно следующие 36 байтов сжатого файла составляют пары (S_i,l_i), показывающие, какие символы встречаются в исходном файле и какова длина кода Хаффмена этих символов. Эту информацию представим табл. 26.

Таблица 26

Символ

E

I

A

F

M

N

S

H

L

O

P

C

D

G

T

U

X

Длина кода Хаффмена

В 39-м и следующих за ним байтах приводятся сами коды Хаффмена всех символов. Чтобы их получить, распишем подробное содержание 39-го и нескольких последующих байтов (табл. 27):

Таблица 27

Для получения кода Хаффмена очередного символа берут столько битов, какова длина этого кода, указанная в предыдущих байтах (табл.26). Все коды Хаффмена представлены в табл. 28.

Таблица 28

Символ исходного файла	Код Хаффмена
E
I
A
F
M
N
S
H
L
O
P
C
D
G
T
U
X

Отметим, что последние три бита в 48-м байте не принадлежат никакому коду Хаффмена и просто добавлены к предыдущим двоичным разрядам, дополняя их до 8. Собственно сжатое сообщение закодировано начиная с 49-го байта (табл. 29).

Таблица 29

Дата добавления: 2015-07-10