
Читайте также:
|
Отличительная черта СИ, имеющего структурную схему прямого преобразования (рис. 11.22), состоит в том, что все преобразования Измерительного сигнала производятся в прямом направлении. Схема состоит из n последовательно соединенных блоков.

Рис. 11.22. Структурная схема прямого преобразования
На схеме через К1, К.,,..., Кn обозначены коэффициенты преобразования блоков. Каждый i-й коэффициент определяется по формуле К = dUi/dUi-1, где
Ui-1 и Ui — входной и выходной сигналы i-го блока.
Входной сигнал Uвх, несущий информацию об измеряемой величине, последовательно преобразуется в промежуточные сигналы U1, U2,..., Un-1 и в выходной сигнал Uвыx. В общем случае каждый из них является переменным во времени и может быть представлен в виде суммы гармонических составляющих. В связи с этим коэффициент Кi должен выражаться комплексным числом, а анализ структурных схем проводиться с использованием теории функций комплексного переменного. Однако для простоты рассмотрения будем считать, что информативным параметром сигнала является только его амплитуда (это чаще всего и бывает на практике). Тогда коэффициенты преобразования выразятся вещественными числами. Предположим также, что коэффициенты преобразования не зависят от уровня сигнала, т.е. звенья считаются линейными: К( = const.
Первоначально считая, что все помехи AUoi (см. рис. 11.22) равны нулю, получим уравнение преобразования СИ, имеющего структурную схему прямого преобразования:
 , (11.10)
, (11.10)
где К — коэффициент преобразования СИ.
На процесс измерения будут оказывать влияние изменения и нестабильность коэффициентов преобразования DКi, а также дрейфы нуля, помехи и наводки, которые в сумме можно описать сигналами DU0i, складываемыми с выходными сигналами каждого блока. Абсолютная погрешность DUвых измерения выходной величины, обусловленная нестабильностью коэффициента преобразования, может быть рассчитана как погрешность косвенного измерения с учетом выражения (11.10):
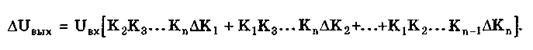
Как видно из этого уравнения, погрешность DUвых является мультипликативной, т.е. зависит от уровня измеряемого сигнала. Относительная мультипликативная погрешность складывается из относительных погрешностей структурных элементов:

где dш = DКi/Кi — относительная нестабильность коэффициента преобразования i-го блока; DК/К - относительная нестабильность коэффициента преобразования СИ.
Рассмотрим погрешность, обусловленную дрейфом нуля и наводками. Дрейф нуля — это изменение сигнала на выходе блока, не связанное с изменением входного сигнала. Он, как правило, определяется при входном сигнале, равном нулю. Дрейф нуля приводит к смещению передаточной функции 1-го элемента (рис. 11.23,а). Результирующее действие сигналов DU0i приводит к появлению дополнительного выходного сигнала
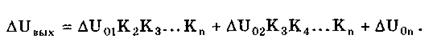
Эта погрешность приведена к выходу СВ и по своей сути является аддитивной.
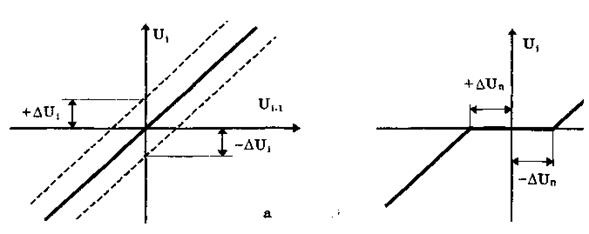
Рис. 11.23. Функции преобразования блоков с дрейфом нуля (а)
и порогом чувствительности (б)
Таким образом, как следует из двух последних уравнений, в СИ, имеющем структурную схему прямого преобразования, происходит суммирование погрешностей, вносимых отдельными блоками. Для достижения высокой точности прибора требуется высокая стабильность параметров и характеристик каждого из блоков. Все это затрудняет реализацию высокоточных СИ по схеме прямого преобразования.
Дата добавления: 2015-07-10; просмотров: 61 | Нарушение авторских прав