Измерении

Если физическая величина проявляется в отношениях эквивалентности, порядка и аддитивности, то она может быть: обнаружена, классифицирована, проконтролирована и измерена. Эти величины, называемые экстенсивными, характеризуют обычно физические вещественные или энергетические свойства объекта, например массу тела, электрическое сопротивление проводника и др.

При измерении экстенсивной величины несчетное множество ее размеров отображается на счетное подмножество в виде совокупности чисел Q, которое также должно удовлетворять отношениям эквивалентности, порядка и аддитивности. Числа Q — это результаты измерений, они могут быть использованы для любых математических операций. Совокупность таких чисел Q должна обладать следующими свойствами:

1. Для проявления в отношении эквивалентности совокупность чисел Q, отображающая различные по размеру однородные величины, должна быть совокупностью одинаково именованных чисел. Это наименование является единицей ФВ или ее доли. Единица физической величины, [Q] — это ФВ фиксированного размера, которой условно присвоено числовое значение, равное единице. Она применяется для количественного выражения однородных ФВ.

2. Для проявления в отношениях эквивалентности и порядка число q_1? отображающее большую по размеру величину Q₁ > Q₂, выбирается большим, чем число q₂, отображающее меньшую по размеру величину Q₂. При этом в обоих случаях используется одна единица ФВ. Для выполнения данного условия в качестве искомой совокупности q,,..., q_n выбирают упорядоченное множество действительных чисел с естественным отношением порядка.

3. Для проявления в отношениях эквивалентности, порядка и аддитивности отвлеченное число, равное оценке суммарной измеряемой величины Q, возникающей в результате сложения составляющих однородных величин Q_i, должно быть равно сумме числовых оценок q_i этих составляющих. Сумма именованных чисел Q_i, отражающих составляющие, должна быть равна именованному числу Q, отражающему суммарную величину:

Если реализовано условие [Q] = [Q_i], т.е. имеет место равенство размеров единиц у всех именованных чисем, отражающих суммарную величину Q и ее составляющие Q_i, то в этом случае вводятся следующие понятия:

значение физической величины Q — это оценка ее размера в виде некоторого числа принятых для нее единиц;

числовое значение физической величины q — отвлеченное число, выражающее отношение значения величины к соответствующей единице данной ФВ.

Уравнение

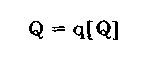
называют основным уравнением измерения. Суть простейшего измерения состоит в сравнении размера ФВ Q с размерами выходной величины регулируемой многозначной меры q[Q]. В результате сравнения устанавливают, что q[Q] < Q < (q + 1)[Q]. Отсюда следует, что q = Int(Q/[Q]), где Int(X) — функция, выделяющая целую часть числа X.

Условием реализации процедуры элементарного прямого измерения является выполнение следующих операций:

• воспроизведение ФВ заданного размера q[Q];

• сравнение измеряемой ФВ Q с воспроизводимой мерой величиной q[Q].

Таким образом, на основе использования общих постулатов эквивалентности, порядка и аддитивности получено понятие прямого измерения, которое может быть сформулировано следующим образом: измерение — познавательный процесс, заключающийся в сравнении путем физического эксперимента данной ФВ с известной ФВ, принятой за единицу измерения.

Ограниченность числового значения q измеряемой величины Q приводит при отображении к гомоморфизму, т.е. к неоднозначности при отображении. Измерение является гомоморфным отображением, так как данному размеру Q в диапазоне от q [Q] до (q+1) [Q] соответствует только одно значение Q₀= q [Q] (рис. 2.3), а данному Q₀ — множество размеров Q в указанном диапазоне.

Рис. 2.3. Гомоморфизм операции измерения

Гомоморфизм вносит вероятностный аспект в отображение не только случайной, но и постоянной величины и является причиной появления неизбежной методической погрешности измерения — погрешности квантования. Эта погрешность возникает из-за принципиального несовершенства измерения как метода отображения непрерывного размера величины числом с ограниченным количеством разрядов.

Дата добавления: 2015-07-10