
Читайте также:
|
Условие прочности при растяжении (сжатии):
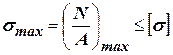 (2.5)
(2.5)
Проектный расчет - определить площадь бруса выполняют по формуле:
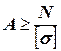 (2.6)
(2.6)
При определении размеров сечения следует использовать рекомендации ГОСТ - а 6636-69.
Проверочный расчет на прочность выполняют по условию:
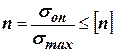 , (2.7)
, (2.7)
где 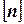 - рекомендуемый коэффициент запаса для заданного материала и для заданных условий работы бруса.
- рекомендуемый коэффициент запаса для заданного материала и для заданных условий работы бруса.
Проверочный и проектный расчеты на жесткость бруса выполняют, используя формулу:
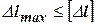 (2.8)
(2.8)
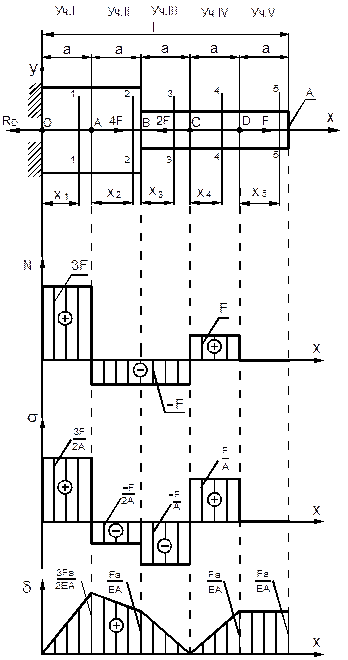 Задача 2. Построить эпюры продольных сил, напряжений и перемещений для бруса, изображенного на рис. 5, и подобрать размеры квадратного поперечного сечения, если заданы
Задача 2. Построить эпюры продольных сил, напряжений и перемещений для бруса, изображенного на рис. 5, и подобрать размеры квадратного поперечного сечения, если заданы 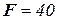 кН,
кН,  см,
см, 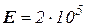 МПа,
МПа, 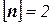 ,
,  мм,
мм,
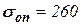 МПа,
МПа, 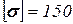 МПа.
МПа.

1. Устанавливаем для бруса в целом систему координат в точку 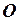 и определяем реакцию в заделке, используя уравнение равновесия:
и определяем реакцию в заделке, используя уравнение равновесия:
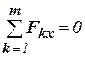
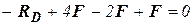 →
→ 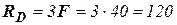 кН.
кН.
2. Разбиваем брус на пять участков, начиная с левого конца бруса, т.к. эпюру перемещений следует строить, начиная от заделки.
3. Устанавливаем для каждого участка свою координатную систему с началом соответственно в точках 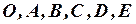 .
.
4. Определение величины продольной силы для каждого участка:
 участок
участок 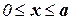 .
.
Проводим сечение 1-1 и отсекаем правую часть бруса. Оставляем левую часть. Составляем уравнение равновесия для оставленной части:
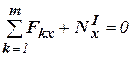 →
→ 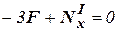 →
→ 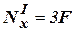 .
. 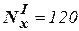 кН.
кН.
Участок 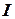 растянут. Величина силы равна:
растянут. Величина силы равна: 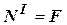 .
.
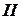 участок
участок 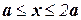 . Проводим сечение 2-2 и отсекаем правую часть бруса. Составляем уравнение равновесия для оставленной левой части:
. Проводим сечение 2-2 и отсекаем правую часть бруса. Составляем уравнение равновесия для оставленной левой части:
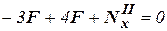 →
→ 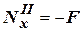 . Проекция силы отрицательная, следовательно, сила направлена в сторону, противоположную нормали. Сечение 2-2 сжато,
. Проекция силы отрицательная, следовательно, сила направлена в сторону, противоположную нормали. Сечение 2-2 сжато, 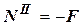 →
→ 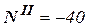 кН.
кН.
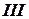 участок
участок 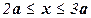 . На этом участке дополнительных внешних сил нет. Он отличается от участка
. На этом участке дополнительных внешних сил нет. Он отличается от участка  только размером сечения. Сечение 3-3 сжато,
только размером сечения. Сечение 3-3 сжато, 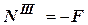 →
→ 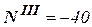 кН.
кН.
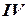 участок
участок 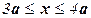 . Проводим сечение 4-4 и отсекаем правую часть бруса.
. Проводим сечение 4-4 и отсекаем правую часть бруса.
Составляем уравнение равновесия для оставленной левой части:
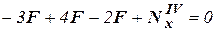 →
→ 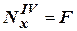 . Сечение 4-4 растянуто,
. Сечение 4-4 растянуто, 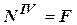 →
→ 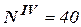 кН.
кН.
 участок
участок 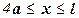 . Проводим сечение 5-5 и отсекаем правую часть бруса.
. Проводим сечение 5-5 и отсекаем правую часть бруса.
Составляем уравнение равновесия для оставленной левой части:
 →
→ 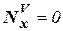 →
→ 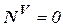
По полученным данным строим эпюру продольных сил (рис.5).
5. Определение площади поперечного сечения на участках бруса из условия (2.6):
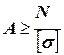 , где
, где 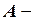 площадь сечения на участках
площадь сечения на участках 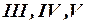 .
.
Дата добавления: 2015-07-10; просмотров: 118 | Нарушение авторских прав