Способ 2 .

1. Разбиваем брус на участки между точками приложения сосредоточенных сил.

В данном случае получим два участка: участок 1 (Уч.1) - OA, участок 2 (Уч.2) – AB.

2. Выбираем начало координат в крайней правой точке 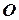бруса.

3. Проводим произвольное сечение 1-1 на первом участке, на расстоянии от начала координат. Отбрасываем левую часть бруса, изображаем продольную силу, направляя вектор 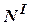по внешней нормали к сечению, и определяем величину из уравнения равновесия для оставленной (правой) части бруса: ,

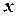где - проекция на ось поперечной силы в сечении на том участке,

- сумма проекций внешних сил, действующих на часть бруса справа от сечения на ось ,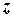

Участок 1 (сечение )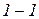

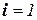
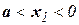
Уравнение (1) примет вид: → .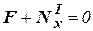

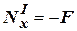Во всех сечениях участка 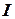, так как внутри всего участка величина продольной силы не зависит от координаты .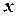

Поскольку , сила 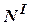направлена против оси 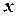, как и показано на рис. 4. Она совпадает по направлению с вектором нормали к сечению 1-1, следовательно, вызывает растяжение бруса. Поэтому .

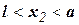
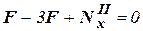
Участок 2 (сечение 2 - 2) . Во всех сечениях второго участка . Поскольку проекция , сила 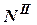совпадает по направлению с осью 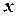и, следовательно, направлена в сторону, противоположную вектору нормали к сечению, вызывая сжатие сечения. Величину силы 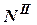по правилу знаков, принятому в сопротивлении материалов, следует считать отрицательной. Следовательно, по величине .

4. Находим силу реакции в заделке, используя уравнение равновесия для участка 2. → → .

5. Строим эпюру продольных сил, откладывая по оси 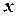координату сечения, по оси - величины поперечных сил. Эпюра показывает, как изменяются внутренние усилия при переходе от сечения к сечению. На участках 1-1 и 2-2 поставлен знак продольной силы, указывающий какой деформации подвержены сечения этих участков. В данном примере участок 1 растянут, а участок 2 – сжат.

В точках приложения сосредоточенных сил на эпюре имеются скачки, равные соответственно силам, приложенным в точках , , .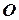

Величина продольной силы может быть определена и по формуле (2):

,

Дата добавления: 2015-07-10