
Читайте также:
|
В реальных опытах присутствуют как систематические, так и случайные ошибки. Пусть они характеризуются стандартными погрешностями sсист и sслуч. Суммарная погрешность находится по формуле
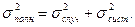 (20)
(20)
Поясним эту формулу. Систематическая и случайная ошибки могут, в зависимости от случая, складываться или вычитаться друг из друга. Как уже говорилось, точность опытов принято характеризовать не максимальной (и не минимальной), а среднеквадратичной погрешностью. Поэтому правильно рассчитанная погрешность должна быть меньше суммы sслуч + sсист и больше их разности sслуч - sсист. Легко видеть, что sполн, определенная формулой (20), удовлетворяет этому условию. В самом деле, все величины s положительные. Поэтому

Знак равенства возникает только в том случае, когда одна из погрешностей равна нулю. Аналогично имеем
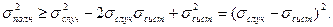
Формула (20) показывает, что при наличии как случайной, так и систематической погрешности полная ошибка опыта больше, чем каждая из них в отдельности, что также является вполне естественным.
Обратим внимание на ещё одну важную особенность формулы (20). Пусть одна из ошибок, например sслуч, в 2 раза меньше другой. Тогда

Как мы уже говорили, погрешности редко удается оценить с точностью лучше 20%. Но в нашем примере с точностью 20% sполн = sсист. Таким образом, меньшая погрешность почти ничего не добавляет к большей, даже если она составляет половину от нее.
Этот вывод очень важен. В том случае, если случайная ошибка опытов вдвое меньше систематической, нет смысла производить многократные измерения, так как полная погрешность опыта при этом практически не уменьшается. Измерения достаточно произвести 2 - 3 раза, чтобы убедиться, что случайная ошибка действительно мала.
Дата добавления: 2015-07-10; просмотров: 74 | Нарушение авторских прав