Процесс измерений

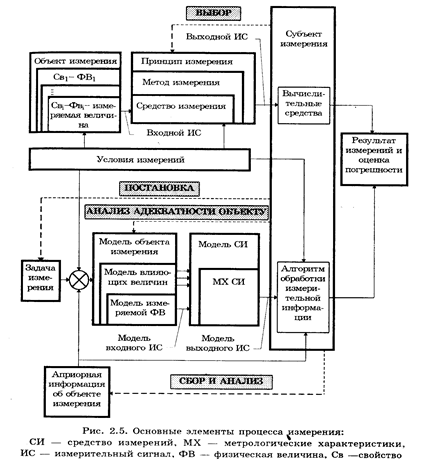
Измерение - сложный процесс, включающий в себя взаимодействие целого ряда его структурных элементов. К ним относятся: измерительная задача, объект измерения, принцип, метод и средство измерения, и его модель, условия измерения, субъект измерения, результат и погрешность измерения. Эти элементы и их взаимосвязи показаны на рис. 2.5 в виде структурной схемы.

Из нее видно, что процесс измерения протекает по двум параллельным ветвям, содержащим соответствующие друг другу элементы, относящиеся к реальности (верхняя ветвь) и её отражению, или познанию (нижняя ветвь). Элементы обеих ветвей, неразрывно связанных между собой, соответствуют друг другу по типу "реальность - отражение (модель)".

Первым начальным элементом каждого измерения является его задача (цель). Задача любого измерения заключается в определении значения выбранной (измеряемой) ФВ с требуемой точностью в заданных условиях. Постановку задачи измерения осуществляет субъект измерения - человек. При постановке задачи конкретизируется объект измерения, в нем выделяется измеряемая ФВ и определяется (задается) требуемая погрешность измерения.

,

Объект измерения - это реальный физический объект, свойства которого характеризуются одной или несколькими измеряемыми ФВ. Он обладает многими свойствами (Св₁..., Св _i, см. рис. 2.5) и находится в многосторонних и сложных связях с другими объектами. Субъект измерения - человек принципиально не в состоянии представить себе объект целиком, во всем многообразии его свойств и связей. Вследствие этого взаимодействие субъекта с объектом возможно только на основе математической модели объекта. Математическая модель объекта измерения - это совокупность математических символов (образов) и отношений между ними, которая адекватно описывает интересующие субъекта свойства объекта измерения.

Модель объекта измерения строится до выполнения измерения в соответствии с решаемой задачей на основе априорной информации об объекте и условиях измерения. На рис. 2.5 это отражено в виде суммирования сведений о цели, условиях измерения и априорной информации об объекте. Модель объекта измерения должна удовлетворять следующим требованиям:

- погрешность, обусловленная несоответствием модели объекту измерения, не должна превышать 10% предельно допускаемой погрешности измерения;

- составляющая погрешности измерения, обусловленная нестабильностью измеряемой ФВ в течение времени, необходимого для проведения измерения, не должна превышать 10% предельно допускаемой погрешности.

Если выбранная модель не удовлетворяет этим требованиям, то следует перейти к другой модели объекта измерений.

Априорная информация, т.е. информация об объекте измерения, известная до проведения измерения, является важнейшим фактором, обуславливающим его эффективность. При полном отсутствии этой информации измерение в принципе невозможно, так как неизвестно, что же необходимо измерить, и, следовательно, нельзя выбрать нужные средства измерений. При наличии априорной информации об объекте в полном объеме, т.е. при известном значении измеряемой величины, измерения попросту не нужны. Указанная информация определяет достижимую точность измерений и их эффективность.

Измеряемая величина определяется как параметр принятой модели, а ее значение, которое можно было бы получить в результате абсолютно точного эксперимента, принимается в качестве истинного значения данной величины. Идеализация, принятая при построении модели объекта измерения, обуславливает несоответствие параметра модели исследуемому свойству объекта. Это несоответствие называют пороговым. Обычно на практике из-за трудности оценивания пороговое несоответствие стремятся сделать пренебрежимо малым.

Цель построения модели объекта измерения состоит в выявлении (представлении) конкретной ФВ, подлежащей определению. Собственно следует говорить не о модели объекта измерения в целом, а о модели его измеряемого свойства или измеряемой ФВ.

Модель объекта измерения необязательно должна быть математической. Ее характер должен определяться видом и свойствами объекта измерений, а также целью измерений. Моделью может служить любое приближенное описание объекта, которое позволяет выделить параметр модели (или функционал параметров), являющейся измеряемой величиной и отряжающий то свойство объекта измерений, которое необходимо оценить для решения измерительной задачи. Модель должна достаточно хорошо отражать две группы свойств (ФВ) объекта измерений: определяемые при измерении и влияющие на результат измерения.

Основной проблемой моделирования объектов измерений является выбор таких моделей, которые можно считать адекватно описывающими измеряемые величины (свойства) данного объекта. Важно отметить, что адекватность модели обуславливается не только теми свойствами объекта, которые требуется определить в рамках данной измерительной задачи, но и теми, которые могут влиять на результаты измерения искомой величины.

Построение адекватных моделей объектов измерений до настоящего времени является сложной творческой и неформализуемой задачей. Ее решение требует высокой квалификации, опыта и, естественно, инженерной интуиции. При этом зачастую приходится решать две взаимоисключающие задачи: модель должна адекватно отражать все свойства объекта, необходимые для решения измерительной задачи, и в то же время быть по возможности простой и содержать минимум параметров.

В большинстве практических инженерных задач модели объектов измерений достаточно очевидны и, как правило, несложны. Объект измерения характеризуется набором свойств и описывающих их ФВ. На рис. 2.5 одна из них (i -я) является измеряемой величиной.

Измеряемая величина - это ФВ, подлежащая определению в соответствии с измерительной задачей. До недавнего времени понятие "физическая величина" считалось достаточным для постановки и решения всех измерительных задач. Однако из-за существенного расширения области применения измерений, усложнения их задач и усиления требований к точности и достоверности в ряде случаев оно перестало удовлетворять потребности в экспериментальном определении различных свойств разнообразных объектов.

При планировании современных измерений требуется введение более конкретных понятий, определяемых целями измерений, чем весьма общего понятия "физическая величина". В настоящее время под измеряемой величиной понимается параметр или функционал параметра модели объекта измерений, отражающий то его свойство, количественную оценку которого необходимо получить в результате измерений. Измеряемая величина всегда имеет размерность определенной ФВ, но представляет собой некоторую ее конкретизацию, обусловленную свойствами объекта измерений, которые связаны с поставленной целью измерений.

Для иллюстрации вышесказанного рассмотрим ряд примеров. Измерительная информация, т.е. информация о значениях измеряемой ФВ, содержится в измерительном сигнале. Измерительный сигнал - это сигнал, содержащий количественную информацию об измеряемой ФВ. Он поступает на вход СИ, при помощи которого преобразуется в выходной сигнал, имеющий форму, удобную либо для непосредственного восприятия человеком (субъектом измерения), либо для последующей обработки и передачи. Субъект измерения осуществляет выбор принципа, метода и средства измерений.

Дата добавления: 2015-07-10