системи довільно розташованих сил

Рівняння рівноваги плоскої

Якщо розглянути рівновагу твердого тіла, що знаходиться в рівновазі під дією плоскої системи сил, то, очевидно, це тіло буде знаходитися в рівновазі лише у тому випадку, якщо головний вектор F_Σ системи сил і її головний момент Μ _Σ будуть дорівнювати нулю.

При розв'язанні задач статики широко використовують аналітичні методи, які вимагають складання рівнянь рівноваги, умови рівнова­ги можна виразити трьома формами рівнянь рівноваги.

Перша /основна/ форма рівнянь. Із формул для визначення головного вектора і головного моменту плоскої системи сил випливає, що вони дорівнюватимуть нулю, якщо:

- тобто для рівноваги плоскої системи сил необхідно і достатньо, щоб сума проекцій усіх сил на кожну з двох координатних осей і алгебраїч­на сума їх моментів відносно будь-якого центра, що лежить у площині дії сил, дорівнювали нулю.

; ;

Другу форму рівнянь рівноваги одержимо, якщо в системі замість одного рівняння моментів складемо два рівняння моментів від­носно будь-яких двох центрів, до яких додамо одне рівняння проекцій усіх званих сил на вісь, не перпендикулярну до прямої, що з’єднує ці центри, тобто де вісь X не перпендикулярна лінії АВ /рис. 4.II/.

Через те, що система сил знаходиться в рівновазі, головний момент цієї системи відносно будь-якої точки площини дорів­нює нулю, зокрема відносно точок А і В. Для рівноваги плоскої сис­теми сил одного рівняння моментів не достатньо, оскільки головний вектор може проходити, наприклад, через точку Д, тоді момент від­носно точки В дорівнює нулю, а відносно точки Д - не дорівнює нулю.

;

Третя форма рівнянь рівноваги наступна. Для рівноваги довільно розташованих сил необхідно і достатньо, щоб алгебраїчна сума моментів усіх сил відносно кожної із трьох

довільних точок площини, які не лежать на одній прямій, дорів­нювала нулю.

Треба зазначити, що в усіх випадках для системи довільно розта­шованих сил можна скласти тільки три незалежних рівняння рівноваги. Тому в задачах повинно бути не більше трьох невідомих.

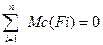
Рис. 1

5.2. Просторова система довільно розташованих сил. Умова рівноваги.

Метод зведення сил до одного центру, який розглянуто для плоскої системи сил,

можна застосувати і для системи сил, як завгодно розташованих у просторі.

Згідно з теоремою Пуансо, будь-яку силу можна
перенести паралельно самій собі у будь-яку точку тіла, додавши при цьому деяку пару. Переносячи кожну із сил просторової системи в одну будь-яку довільну точку 0 /центр зведення/, одержують просторову систему збіжних у цій точці сил і систему приєднаних пар сил, розташова­них у різних площинах.

Систему збіжних сил заміняють однією еквівалентною їм силою F_Σ, яку називають головним вектором просторової системи сил. Головний вектор F_Σ визначається формулою:

Головний момент М_Σ визначаємо за формулою:

Умовою рівноваги просторової системи довільно розташованих сил є те, що головний вектор і головний момент дорівнюють 0. Тому слід складати шість рівнянь рівноваги.

Дата добавления: 2015-07-10