Расчет балки настила. Расчетная схема балки настила представлена на рис

Расчетная схема балки настила представлена на рис. 4.11. Пролет балки настила l = B = 6 м.

Рис. 4.11. Расчетная схема балки настила (3-й вариант)

Определяем нормативную и расчетную нагрузки.

Нормативная нагрузка на балку принимается равномерно распределенной:

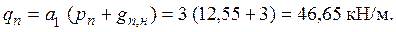
Расчетная нагрузка

где g _{¦ g} = 1,1 – коэффициент надежности по нагрузке для постоянной нагрузки от железобетонных плит.

Расчетный изгибающий момент

Максимальная поперечная сила

Требуемый момент сопротивления поперечного сечения балки при работе с учетом упругопластических деформаций

По сортаменту выбираем ближайший номер двутавра, у которого W_x > W_{n, min}. Принимаем I 40, имеющий момент сопротивления W_x = 953 см³; статический момент полусечения S_x = 545 см³; момент инерции сечения I_x = 19062 см⁴; площадь сечения А = 72,6 см²; ширину пояса b_f = 155 мм; толщину пояса t_f = 13 мм; толщину стенки t_w = 8,3 мм; линейную плотность (массу 1 м пог.) 57 кг/м.

Уточнение коэффициента с ₁, M и Q c учетом собственного веса балки настила.

Площадь пояса

Площадь стенки

Отношение

A_f / A_w = 20,15 / 32,3 = 0,62.

По табл. 4.2 определяем коэффициент с ₁ = 1,108.

Равномерно распределенная нагрузка от собственного веса балки настила длиной 1 м

q_{n , бн} = 57 кг/м = 0,57 кН/м.

Нормативная нагрузка на балку настила

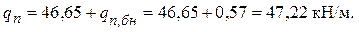
Расчетная нагрузка

Расчетный изгибающий момент

Максимальная поперечная сила

Дата добавления: 2015-07-10