расчетно-проектировочной работе

СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ

Методическое указание к

расчетно-проектировочной работе

«Расчет балки постоянного сечения при плоском изгибе»

Набережные Челны

В данной расчетно-проектировочной работе проводится расчет балки постоянного сечения на прочность и жесткость при плоском изгибе.

Изгиб балки называется плоским, если действую­щие на нее внешние силы и моменты находятся в плоскости, проходящей через одну из главных центральных осей инерции поперечного сечения балки. При плоском изгибе в поперечных сечениях балки возникают изгибающий момент M_y, поперечная сила Q_z и связанные с ними нормальные

(1)

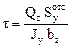(2)

и касательные напряжения. В формулах (1), (2):

J_y - осевой момент инерции сечения;

- статический момент отсеченной части;

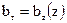- ширина сечения.

Расчет балки на прочность проводится по максимальным нормальным 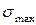и касательным напряжениям, а также с использованием теорий прочности. В данной работе используются соотношения третьей или четвертой теории прочности.

Условия прочности по максимальным напряжениям представляется следующим образом:

(3)

(4)

где - допускаемые значения напряжений.

Соотношения третьей и четвертой теорий прочности, соответственно, имеют вид

(5)

(6)

В работе проводится расчет на прочность балки двутаврового стандартного профиля. Из условий прочности по максимальным нормальным напряжениям (3) находится номер двутавра, для которого проверяется выполнение условий (4), а также (5) или (6). Если одно из условий нарушается, то номер двутавра следует увеличить до величины, при которой выполняются все условия прочности.

При вычислении левых частей неравенств (3)-(6) следует использовать значения M_y, Q_z возникающие в так называемых опасных (наиболее напряженных) сечениях.

Для определения опасных сечений строятся эпюры M_y, Q_z.

При расчете по максимальным нормальным напряжениям 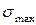опасным является сечение, в котором M_y принимает наибольшее значение.

При расчете по максимальным касательным напряжениям опасным является сечение, в котором Q_z принимает наибольшее значение.

В случае использования соотношений (5), (6) опасным является сечение, в котором наибольшее значение принимают M_y и Q_z. Если наибольшие значения M_y и Q_z возникают в различных сечениях, то выполнение условий (5), (6) следует проверить для сечений, в которых M_y и Q_z значительны по величине.

Напряжения σ и τ изменяются по высоте сечения. В условия прочности представляются значениями σ и τ, возникающие в наиболее напряженной точке сечения, для определения которой строят эпюры σ и τ в опасном сечении. Наиболее напряженной точкой сечения будет точка, в которой возникают максимальные значения σ и τ. Если наибольшие значения σ и τ возникают в различных точках, то условия (3), (4) записываются в соответствующих точках максимума σ и τ, а условия (5), (6) следует проверить для точек, в которых σ и τ значительны по величине. Для двутаврового сечения это точки перехода от полок к стенке, в которых σ и τ близки к своим максимальным значениям.

Для балок постоянного сечения можно записать уравнение, выражающее зависимость между прогибом балки W и действующими на неё внешними силами и моментами. Это уравнение называется универсальным уравнением упругой линии балки. Аналогичное уравнение можно записать и для углов поворота балки θ.

Дифференциальное уравнение упругой линии балки имеет вид

, (7)

где М_у(х) изгибающий момент в сечении x от начала балки, а EJ_y жесткость сечения при изгибе.

Введем обобщенную функцию

. (8)

Выберем начало системы координат на левом (или правом) конце балки. От начала системы координат разбиваем балку на участки и на последнем участке проводим сечение x. Определяем изгибающий момент М_у(х) в выбранном сечении. При этом следует обратить внимание на особенности учета распределенной нагрузки q. Здесь неявно предполагается, что распределенная нагрузка действует до конца балки непрерывно. Поэтому, если распределенная нагрузка обрывается до конца балки, то следует ее догрузить искусственно и ввести такую же компенсирующую с противоположным знаком, чтобы не изменилась суммарная нагрузка.

Так, например, для балки AB (рис. 1), загруженной сосредоточенными силами P₁, P₂, моментом m₀ и распределенной нагрузкой q выражение М_у(х) имеет вид

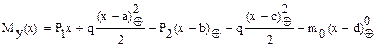. (9)

Подставим (9) в (7), имеем

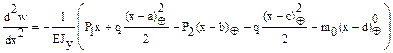.(10)

Полагая EJ_y=const и учитывая 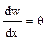, интегрируем (10). Получаем уравнение для угла поворота θ:

.(11)

После повторного интегрирования (11) получаем уравнение прогиба W:

(12)

В уравнениях (11), (12) θ₀ и W₀ – постоянные интегрирования, которые равны соответственно углу поворота и прогибу в начале системы координат (начальные параметры), и определяются из граничных условий (условий закрепления балки).

ПРИМЕР РАСЧЕТА.

Для балки с постоянным поперечным сечением в виде двутавра, схема которой приведена на рис.2, необходимо произвести следующие расчеты:

Из условия прочности по максимальным нормативным напряжениям подобрать размеры поперечного сечения балки. Проверить выполнение условий прочности по максимальным касательным напряжениям и условий третьей или четвертой теории прочности.

Записать универсальное уравнение упругой линии балки и уравнение для углов поворота балки. Построить эпюры прогибов и углов поворота.

Произвести расчет на жесткость по максимальным прогибам в пролете и на консольной части балки.

Дано: l₁=2 м, l₂=4 м, l₃=2 м, q₁=50 кН/м, q₂=30 кН/м, m₀ =40 кН·м, F = 30 кН.

Е=2·10⁵ МПа, σ_adm=160 МПа, τ_adm=100 МПа.

Допускаемые значения прогиба балки в пролете

,

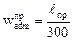а на консоли

,

где , – соответственно, длина пролета и консоли балки.

1. Определение опорных реакций.

Опорные реакции R_В и R_С определяются из уравнений равновесия моментов относительно точек В и С.

.

Следовательно,

.

Из последнего уравнения получаем

.

Для проверки правильности определения реакции R_В и R_С составим уравнение равновесия в виде проекций всех сил на ось Z.

.

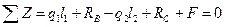Подставляя числовые значения параметров, находим

50·2-70-30·4+60+30=0, 190-190=0.

Уравнение равновесия удовлетворяется, следовательно, реакции определены правильно.

2. Построение эпюр изгибающего момента M_y и поперечной силы Q_z.

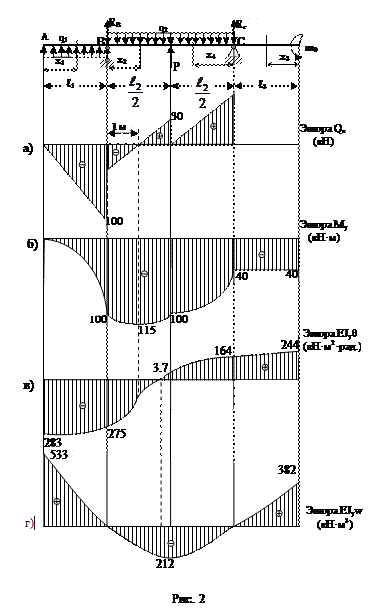
В рассматриваемом случае на балке имеется четыре характерных участка нагружения, которые обозначим, соответственно, как участки I, II, III, IV (рис.2).

Участок I 0 ≤ х₁ ≤ 2м.

, .

При х₁ = 0; M_y = 0; Q_z = 0;

х₁ = 2; M_y = -100 кН/м; Q_z = -100кН.

Участок II 0 ≤ х₂ ≤ 2м.

, .

При х₂ = 0; M_y = -100 кН·м; Q_z = -30кН;

х₂ = 2; M_y = -100 кН·м; Q_z = 30кН.

Из полученных числовых данных видно, что изгибающий момент M_y принимает на данном участке экстремальное значение. Определим максимальное значение M_y и сечения, в котором он возникает ­– x₀₂.

Из условия экстремума , имеем

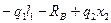=0, .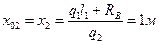

M_y(x₀₂)_max = -115кН.

Участок III 0 ≤ х₄ ≤ 2

M_y = -m₀= -40 кН·м, Q_z = 0.

Участок IV 0 ≤ х₃≤ 2м.

; .

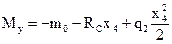При х₄ = 0; M_y = -40 кН·м; Q_z = 60кН;

x₄ = 2; M_y = -100 кН·м; Q_z = 0.

На основе полученных числовых результатов строятся эпюры Q_z, M_y (рис.2 а, б).

3. Подбор сечения балки из условия прочности по максимальным нормальным напряжениям.

Как видно из эпюры M_y (рис.2), опасным сечением при расчете по максимальным нормальным напряжениями является сечение при х = 3м, в котором возникает наибольшее значение изгибающего момента .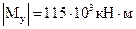

Из условия прочности (3) получаем момент сопротивления сечения балки

. (13)

В соответствии с таблицей сортамента, найденному в (13) значению W_y наиболее соответствует двутавр № 36 моментом сопротивления W_y=743 см³.

Для двутавра № 36

h = 36 см; b = 14,5 см; d = 0,75 см; t = 1,23 см; J_y = 13380 см⁴; =423 см³.

4. Проверка прочности двутавра по максимальному касательному напряжению и с использованием теории прочности.

В сечении, проходящем через точку В, возникает наибольшая поперечная сила 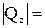100 кН, поэтому это сечение будет опасным сечением при расчете по максимальным касательным напряжениям.

Проверку прочности двутавра по третьей теории прочности проведем также для сечения в точке В, так как здесь Q_z = Q_{z max}, а изгибающий момент принимает сравнительно большое значение 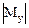= 100 кН·м.

Для определения наиболее напряженной точки в сечении, построим эпюры напряжений σ и τ.

В соответствии с формулой (1) σ изменяется по высоте сечения, по линейному закону.

При ; ;

;

z = 0; .

Что же касается вычисления касательных напряжений в пределах полок двутавра при 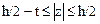, то пользоваться формулой (2) нельзя, так как эти напряжения не одинаковы по ширине полки. На площадках вблизи оси z можно предположить, что они меняются примерно по линейному закону. На площадках же, расположенных в остальной части полок, т.е. почти по всей ширине, изменяются по параболическому закону. При этом из-за условий на поверхности полок и в силу закона о парности касательных напряжений, они не могут иметь большие значения. А при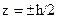 =0 и, следовательно, τ=0.

Если , то b_z = d и .

Следовательно, касательные напряжения, определяемые формулой (2), по высоте стенки меняются по параболическому закону, достигая наибольшей величины на нейтральной оси сечения:

Таким образом, условие прочности по касательным напряжениям выполняется.

При расчете по главным напряжениям следует учесть, что полки двутавра воспринимают нормальные напряжения, имеющее наибольшее или близкое к нему значение, а касательные напряжения в полках двутавра малы. В стенках двутавра по мере приближения к нейтральной оси нормальные напряжения стремятся нулю. Величина статического момента при различных значениях z в пределах стенки меняется мало. Поэтому касательные напряжения по всей высоте стенки достаточно велики.

На основании вышеизложенного, имеем:

при 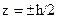τ=0;

при , а ;

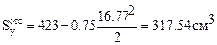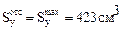при z=0 , а .

По полученным результатам строим эпюры σ и τ по высоте сечения (рис. 3).

42.15

Проверку выполнения условия теории прочности проведем для точек ± , т.к. в этой точках úσç= 125,3 МПа и÷τç=31,64 МПа значительны по величине.

Воспользуемся соотношениями третьей теории прочности (5), получим

.

Условие третьей теории прочности выполняется.

5. Универсальное уравнение упругой линии балки и уравнение для углов поворота балки.

Начало системы координат выберем на левом конце балки. Проведем сечение на последнем участке. В связи с тем, что распределенная нагрузка q₁ обрывается на втором участке, продолжаем ее пунктирно до конца балки и сверху добавим равнодействующую. Аналогично поступаем и с q₂ от токи С до конца балки (рис.4).

Определяем изгибающий момент M_y(x) в сечении.

(14)

Подставляем (13) в уравнение (7)

(15)

и интегрируем дважды:

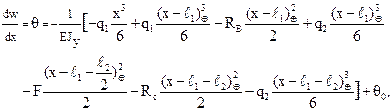(16)

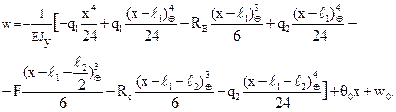(17)

θ₀ и w₀ определяем из граничных условий:

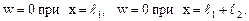(18)

Подставляя выражения для прогиба (17) в условия (18), получим систему уравнений

которая преобразуется к виду

(19)

Решение системы уравнений (19):

Итого, имеем

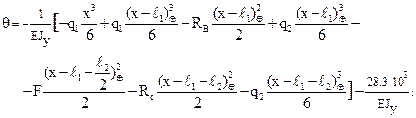
(20)

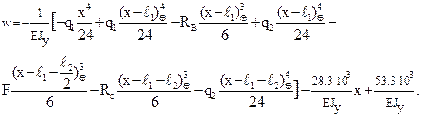
(21)

Для построения эпюр прогибов и углов поворота вычисляем их значения, увеличенные в EJ_y раз. Полученные числовые результаты представлены в таблице 1. С использованием этих данных построены графики изменения по длине балки EJ_yθ и EJ_yw (рис. 2 в, г).

Таблица 1

х (м)
EJyθ (кН·м^2)	-283	-275	-217	-106	3.7
EJyw (кН·м^3)				-162	-212	-160

6. расчет балки на жесткость.

При определении наибольших значений прогибов в пролете и на консолях балки используем график для EJ_yw.

В пролете балки BC

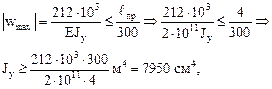
что соответствует двутавру №33.

На левой консоли AB

что соответствует двутавру №45.

На правой консоли CD

что соответствует двутавру №40.

Следовательно, из условия жесткости требуется двутавр №45.

Окончательно, для удовлетворения условий, как прочности, так и жесткости необходимо выбрать двутавр №45.

Дата добавления: 2015-07-10