Вопрос 4. Параметрический резонанс.

Внешнее воздействие на колебательную систему может сводиться к периодическому изменению параметров самой колебательной системы. Возбуждаемые таким образом колебания называются параметрическими, а сам механизм – параметрическим резонансом.

Прежде всего, попытаемся ответить на вопрос: можно ли раскачать уже имеющиеся в системе малые колебания, периодически изменяя определенным образом какой-либо ее параметр.

В качестве примера рассмотрим раскачивание человека на качелях. Сгибая и выпрямляя ноги в «нужные» моменты, он фактически изменяет длину маятника. В крайних положениях человек приседает, тем самым чуть-чуть опускает центр тяжести колебательной системы, в среднем положении человек выпрямляется, поднимая центр тяжести системы.

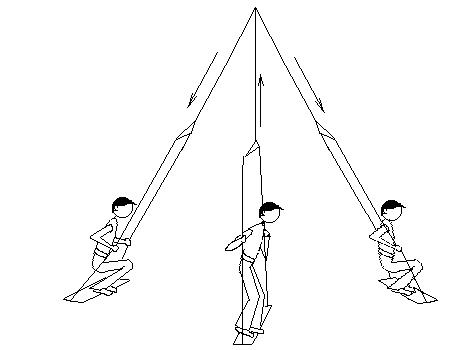Чтобы понять, почему при этом человек раскачивается, рассмотрим предельно упрощенную модель человека на качелях – обычный небольшой маятник, то есть небольшой грузик на легкой и длинной нити. Чтобы имитировать поднимание и опускание центра тяжести, пропустим верхний конец нити через маленькое отверстие и будем вытягивать нить в те моменты, когда маятник проходит положение равновесия, и настолько же опускать нить, когда маятник проходит крайнее положение.

Подтягивая маятник в нижней точке траектории, мы совершаем положительную работу

В крайнем положении

Работа силы натяжения нити за период (с учетом того, что подъем груза и его опускание производится два раза за период и что D l << l):

Обратите внимание, что в скобках стоит не что иное, как утроенная энергия колебательной системы. Кстати, это величина положительная, следовательно, работа силы натяжения (наша работа) положительная, она приводит к увеличению полной энергии системы, а значит, к раскачке маятника.

Интересно, что относительное изменение энергии за период не зависит от того, слабо раскачивается маятник или сильно. Это очень важно, и вот почему. Если маятник «не подкачивать» энергией, то за каждый период он будет терять за счет силы трения определенную часть своей энергии, и колебания будут затухать. А чтобы размах колебаний увеличивался, необходимо, чтобы приобретаемая энергия превышала потерянную на преодоление трения. И это условие, оказывается, одно и то же – как при маленькой амплитуде, так и при большой.

Например, если за один период энергия свободных колебаний уменьшается на 6%, то для того, чтобы колебания маятника длиной 1 м не затухали, достаточно в среднем положении уменьшать его длину на 1 см, а в крайнем – на столько же увеличивать.

Возвращаясь к качелям: если вы начали раскачиваться, то нет необходимости приседать все глубже и глубже – приседайте все время одинаково, и будете взлетать все выше и выше!

*** Опять добротность!

Как мы уже сказали, для параметрической раскачки колебаний необходимо выполнение условия DЕ > А_{трения за период}.

Найдем работу силы трения за период

Видно, что относительная величина подъема маятника для его раскачки определяется добротностью системы.

---

Дата добавления: 2015-07-10