Вопрос 1. Вынуждающая сила изменяется по гармоническому закону.

При выведении колебательной системы из положения равновесия в ней будут действовать: квазиупругая сила F_х = - kx, сила сопротивления F_сопрх = - rv_x и вынуждающая сила F_вын = F₀sin wt.

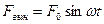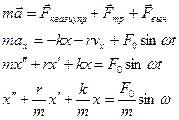Второй закон Ньютона запишется в виде:

Введя обычные обозначения,,, получим дифференциальное уравнение

***

Решение уравнения (1) ищут в виде, где - это решение уравнения (1), если бы в нем не было правой части. Видно, что без правой части уравнение превращается в известное нам уравнение затухающих колебаний, решение которого мы уже знаем. За достаточно большое время свободные колебания, которые возникнут в системе при выведении ее из положения равновесия, практически затухнут, и в решении уравнения останется только второе слагаемое. Будем искать это решение в виде

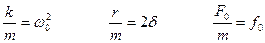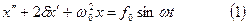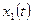
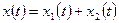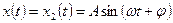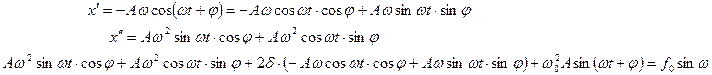
Вычисли первую и вторую производную от x(t) и подставим их в уравнение (1):

Сгруппируем слагаемые иначе:

Это равенство должно выполняться в любой момент времени t, что возможно только, если коэффициенты при синусе и косинусе равны нулю.

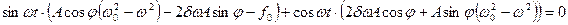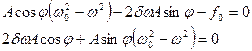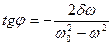Из второго уравнения получаем. Этому значению должно удовлетворять j, чтобы x₂(t) было решением уравнения (1).

Для определения неизвестного А возведем оба полученных нами уравнения в квадрат и сложим. Решая полученное равенство относительно А, найдем:

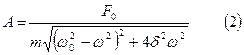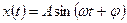
Анализ полученного результата:

Итак, тело, на которое действует вынуждающая сила, меняющаяся по гармоническому закону, совершает колебательное движение с частотой вынуждающей силы.

Разберем подробнее вопрос об амплитуде вынужденных колебаний:

1. Амплитуда установившихся вынужденных колебаний не меняется с течением времени. (Сравните с амплитудой свободных затухающих колебаний).

2. Амплитуда вынужденных колебаний прямо пропорциональна амплитуде вынуждающей силы.

3. Амплитуда зависит от трения в системе (А зависит от d, а коэффициент затухания d, в свою очередь, зависит от коэффициента сопротивления r). Чем больше трение в системе, тем амплитуда вынужденных колебаний меньше.

4. Амплитуда вынужденных колебаний зависит от частоты вынуждающей силы w. Как? Исследуем функцию А(w).

·

При w = 0 (постоянная сила действует на колебательную систему) смещение тела неизменно с течением времени (надо иметь в виду то, что это относится к установившемуся состоянию, когда собственные колебания уже практически затухли).

· При w ® ¥, то, как нетрудно видеть, амплитуда А стремится к нулю.

· Очевидно, что при какой-то частоте вынуждающей силы амплитуда вынужденных колебаний примет наибольшее значение (для данного d). Явление резкого возрастания амплитуды вынужденных колебаний при определенном значении частоты вынуждающей силы носит название механического резонанса.

Найдем резонансную частоту w_рез. Для этого найдем минимум выражения, стоящего под корнем в знаменателе дроби (2). Продифференцировав это выражение по w и приравняв к нулю, получим:

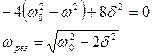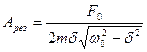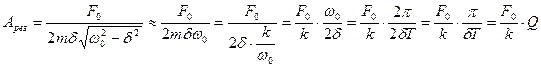Интересно, что добротность колебательной системы в этом случае показывает во сколько раз резонансная амплитуда превышает смещение тела от положения равновесия под действием постоянной силы F₀.

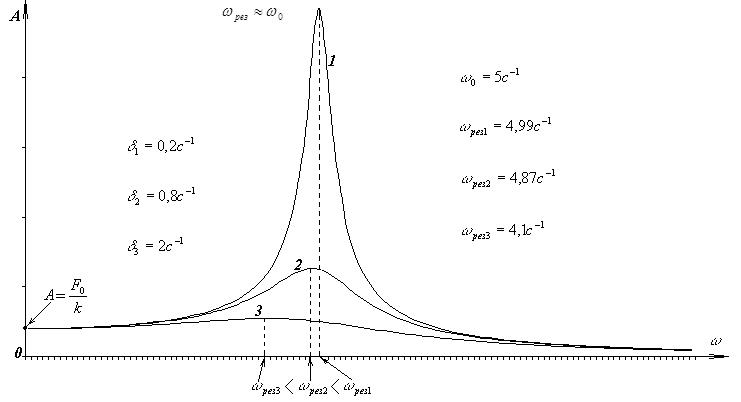
Мы видим, что и резонансная частота, и резонансная амплитуда зависят от коэффициента затухания d. С уменьшением d к нулю резонансная частота возрастает и стремится к частоте собственных колебаний системы w₀. При этом резонансная амплитуда возрастает и при d = 0 обращается в бесконечность. Разумеется, на практике амплитуда колебаний бесконечной быть не может, так как в реальных колебательных системах всегда действуют силы сопротивления. Если система имеет малое затухание, то приближенно можно считать, что резонанс наступает при частоте собственных колебаний.:

При больших значениях коэффициента затухания резонансные явления исчезают. Амплитуда вынужденных колебаний монотонно убывает.

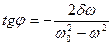Вернемся к вопросу о фазе вынужденных колебаний.

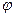в рассматриваемом случае - это сдвиг по фазе между вынуждающей силой и смещением тела от положения равновесия.

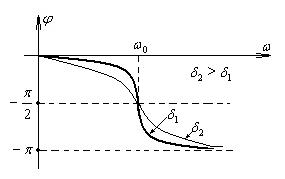
Нетрудно видеть, что сдвиг по фазе между силой и смещением зависит от трения в системе 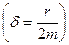и частоты внешней вынуждающей силы 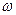. Эта зависимость показана на рисунке. Видно, что при 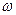< 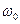тангенс принимает отрицательные значения, а при 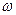> 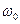- положительные.

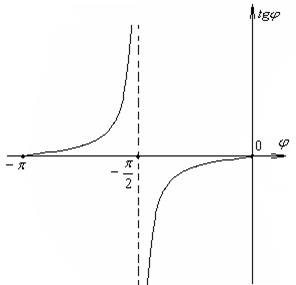
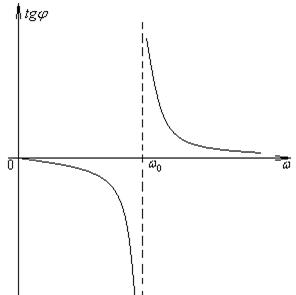
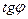Зная зависимость от угла 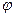, можно получить зависимость 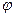от частоты вынуждающей силы .

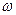При частотах внешней силы, существенно меньших собственной, смещение отстает по фазе от вынуждающей силы незначительно. При увеличении частоты внешней силы это запаздывание по фазе растет. При резонансе 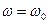(если 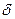невелико) сдвиг по фазе становится равным 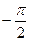. При 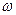>> 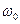колебания смещения и силы происходят в противофазе. Такая зависимость может показаться на первый взгляд странной. Чтобы понять этот факт, обратимся к энергетическим преобразованиям в процессе вынужденных колебаний.

---

Дата добавления: 2015-07-10