Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Уравнения и схемы замещения трансформатора

⇐ ПредыдущаяСтр 18 из 38Следующая ⇒


Читайте также:
  1. II.7.4. Оптические схемы спектральных приборов
  2. Абстрактно-логические схемы.
  3. Автотрансформаторы, схемы включения обмоток, энергетическая эффективность.
  4. Блок-схемы
  5. Блок-схемы алгоритмов
  6. В.13. Задача Коши для уравнения колебания струны. Формула Даламбера.
  7. В.14. Постановка краевых задач для уравнения теплопроводности. Метод разделения переменных для решения первой краевой задачи.

С целью упрощения математического описания процессов сложную картину магнитного поля трансформатора удобно представить в виде главного поля (поля взаимной индукции с потоком Ф) и поля рассеяния (рис. 6.1). Поток взаимной индукции замыкается по магнитопроводу, сцепляется с обеими обмотками и наводит в них ЭДС Е1 и Е 2. Потоки рассеяния первичной Фs1 и вторичной Фs2 обмоток сцепляются с каждой из обмоток в отдельности и наводят в них ЭДС рассеяния Еs1 и Еs2. Эти ЭДС можно выразить через соответствующие индуктивные сопротивления взаимной индукции х12 и рассеяния xs 1 и xs2 первичной и вторичной обмоток:

, ,

, .

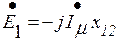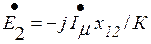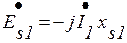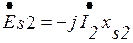Для удобства расчётов условно выравнивают (приводят) числа витков обмоток (w¢2 = w1) при условии сохранения магнитных полей и мощностей. Все величины вторичной обмотки, приведённой к числу витков первичной, снабжают дополнительным индексом (штрихом сверху).

Уравнения напряжений и токов приведённого трансформатора имеют вид

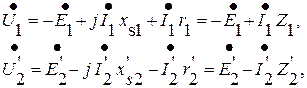(6.1)

,

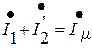где r1, r¢2 - активные сопротивления первичной и приведённой вторичной обмотки, Z1, Z¢2 - полные комплексные сопротивления первичной и приведённой вторичной обмоток.

Величины приведённой и реальной вторичной обмотки связаны следующими соотношениями:

U¢2 = U2 K, E¢2= E2 K= Е1, I¢2 = I2 / K,

x¢s2= xs2 K2, r¢2= r2 K2, Z¢2 = Z2K2.

 

Для учёта магнитных потерь (потерь в стали магнитопровода от вихревых токов и гистерезиса) вводится активное сопротивление rμ, потери в котором численно равны магнитным потерям 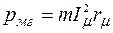, где m – число фаз трансформатора.

В «приведённом» трансформаторе ЭДС обмоток можно записать как падения напряжения на индуктивном сопротивлении х¢12 взаимной индукции

 

,

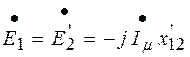а с учётом магнитных потерь

.

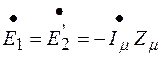Здесь 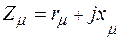, 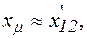а сопротивление rμ учитывает наличие потерь в стали магнитопровода.

Схема замещения трансформатора с учётом магнитных потерь в соответствии с уравнениями (6.1) принимает вид, показанный на рис. 6.2. Уравнения (6.1) и схема замещения соответствуют одной фазе трансформатора в установившихся симметричных режимах работы.

Параметры схемы замещения выражают в относительных единицах: Zm* = Zm/Zб, r¢2* = r¢2 / Zб, xs1* = x s1 / Zб и т.д., где базисное сопротивление Zб = UНФ/IНФ.

Дата добавления: 2015-07-10; просмотров: 97 | Нарушение авторских прав

⇐ Предыдущая11121314151617181920212223242526Следующая ⇒



mybiblioteka.su - 2015-2024 год. (0.007 сек.)